Tipping Points of Evolving Epidemiological Networks: Machine Learning-Assisted, Data-Driven Effective Modeling

We study the tipping point collective dynamics of an adaptive susceptible-infected-susceptible (SIS) epidemiological network in a data-driven, machine learning-assisted manner. We identify a parameter-dependent effective stochastic differential equation (eSDE) in terms of physically meaningful coarse mean-field variables through a deep-learning ResNet architecture inspired by numerical stochastic integrators. We construct an approximate effective bifurcation diagram based on the identified drift term of the eSDE and contrast it with the mean-field SIS model bifurcation diagram. We observe a subcritical Hopf bifurcation in the evolving network's effective SIS dynamics, that causes the tipping point behavior; this takes the form of large amplitude collective oscillations that spontaneously -- yet rarely -- arise from the neighborhood of a (noisy) stationary state. We study the statistics of these rare events both through repeated brute force simulations and by using established mathematical/computational tools exploiting the right-hand-side of the identified SDE. We demonstrate that such a collective SDE can also be identified (and the rare events computations also performed) in terms of data-driven coarse observables, obtained here via manifold learning techniques, in particular Diffusion Maps. The workflow of our study is straightforwardly applicable to other complex dynamics problems exhibiting tipping point dynamics.

Learning effective stochastic differential equations from microscopic simulations: combining stochastic numerics and deep learning

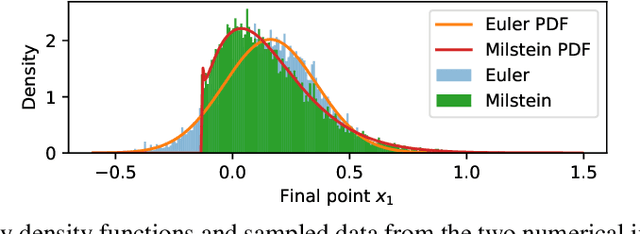
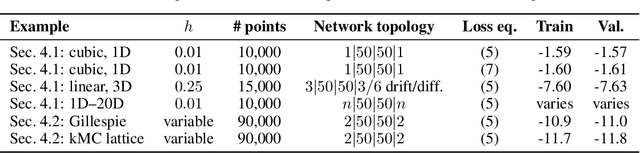
We identify effective stochastic differential equations (SDE) for coarse observables of fine-grained particle- or agent-based simulations; these SDE then provide coarse surrogate models of the fine scale dynamics. We approximate the drift and diffusivity functions in these effective SDE through neural networks, which can be thought of as effective stochastic ResNets. The loss function is inspired by, and embodies, the structure of established stochastic numerical integrators (here, Euler-Maruyama and Milstein); our approximations can thus benefit from error analysis of these underlying numerical schemes. They also lend themselves naturally to "physics-informed" gray-box identification when approximate coarse models, such as mean field equations, are available. Our approach does not require long trajectories, works on scattered snapshot data, and is designed to naturally handle different time steps per snapshot. We consider both the case where the coarse collective observables are known in advance, as well as the case where they must be found in a data-driven manner.