Gaussian Measures Conditioned on Nonlinear Observations: Consistency, MAP Estimators, and Simulation

The article presents a systematic study of the problem of conditioning a Gaussian random variable $\xi$ on nonlinear observations of the form $F \circ \phi(\xi)$ where $\phi: \mathcal{X} \to \mathbb{R}^N$ is a bounded linear operator and $F$ is nonlinear. Such problems arise in the context of Bayesian inference and recent machine learning-inspired PDE solvers. We give a representer theorem for the conditioned random variable $\xi \mid F\circ \phi(\xi)$, stating that it decomposes as the sum of an infinite-dimensional Gaussian (which is identified analytically) as well as a finite-dimensional non-Gaussian measure. We also introduce a novel notion of the mode of a conditional measure by taking the limit of the natural relaxation of the problem, to which we can apply the existing notion of maximum a posteriori estimators of posterior measures. Finally, we introduce a variant of the Laplace approximation for the efficient simulation of the aforementioned conditioned Gaussian random variables towards uncertainty quantification.

Sampling via Gradient Flows in the Space of Probability Measures

Sampling a target probability distribution with an unknown normalization constant is a fundamental challenge in computational science and engineering. Recent work shows that algorithms derived by considering gradient flows in the space of probability measures open up new avenues for algorithm development. This paper makes three contributions to this sampling approach by scrutinizing the design components of such gradient flows. Any instantiation of a gradient flow for sampling needs an energy functional and a metric to determine the flow, as well as numerical approximations of the flow to derive algorithms. Our first contribution is to show that the Kullback-Leibler divergence, as an energy functional, has the unique property (among all f-divergences) that gradient flows resulting from it do not depend on the normalization constant of the target distribution. Our second contribution is to study the choice of metric from the perspective of invariance. The Fisher-Rao metric is known as the unique choice (up to scaling) that is diffeomorphism invariant. As a computationally tractable alternative, we introduce a relaxed, affine invariance property for the metrics and gradient flows. In particular, we construct various affine invariant Wasserstein and Stein gradient flows. Affine invariant gradient flows are shown to behave more favorably than their non-affine-invariant counterparts when sampling highly anisotropic distributions, in theory and by using particle methods. Our third contribution is to study, and develop efficient algorithms based on Gaussian approximations of the gradient flows; this leads to an alternative to particle methods. We establish connections between various Gaussian approximate gradient flows, discuss their relation to gradient methods arising from parametric variational inference, and study their convergence properties both theoretically and numerically.

Error Analysis of Kernel/GP Methods for Nonlinear and Parametric PDEs

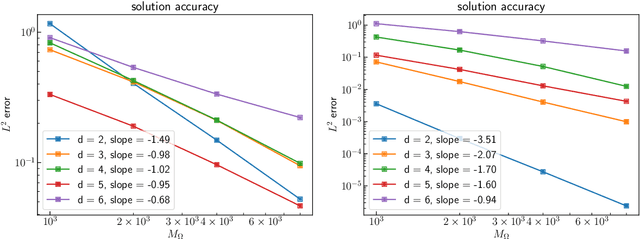
We introduce a priori Sobolev-space error estimates for the solution of nonlinear, and possibly parametric, PDEs using Gaussian process and kernel based methods. The primary assumptions are: (1) a continuous embedding of the reproducing kernel Hilbert space of the kernel into a Sobolev space of sufficient regularity; and (2) the stability of the differential operator and the solution map of the PDE between corresponding Sobolev spaces. The proof is articulated around Sobolev norm error estimates for kernel interpolants and relies on the minimizing norm property of the solution. The error estimates demonstrate dimension-benign convergence rates if the solution space of the PDE is smooth enough. We illustrate these points with applications to high-dimensional nonlinear elliptic PDEs and parametric PDEs. Although some recent machine learning methods have been presented as breaking the curse of dimensionality in solving high-dimensional PDEs, our analysis suggests a more nuanced picture: there is a trade-off between the regularity of the solution and the presence of the curse of dimensionality. Therefore, our results are in line with the understanding that the curse is absent when the solution is regular enough.

Solving and Learning Nonlinear PDEs with Gaussian Processes

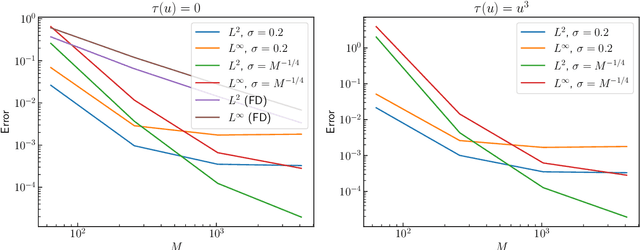
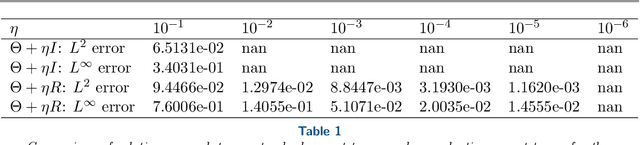
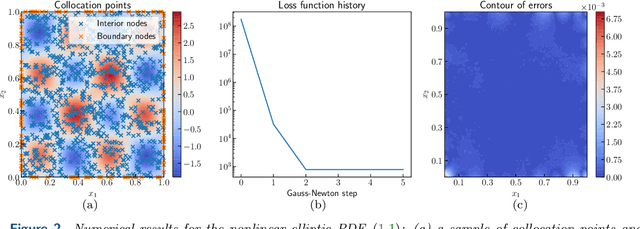
We introduce a simple, rigorous, and unified framework for solving nonlinear partial differential equations (PDEs), and for solving inverse problems (IPs) involving the identification of parameters in PDEs, using the framework of Gaussian processes. The proposed approach (1) provides a natural generalization of collocation kernel methods to nonlinear PDEs and IPs, (2) has guaranteed convergence with a path to compute error bounds in the PDE setting, and (3) inherits the state-of-the-art computational complexity of linear solvers for dense kernel matrices. The main idea of our method is to approximate the solution of a given PDE with a MAP estimator of a Gaussian process given the observation of the PDE at a finite number of collocation points. Although this optimization problem is infinite-dimensional, it can be reduced to a finite-dimensional one by introducing additional variables corresponding to the values of the derivatives of the solution at collocation points; this generalizes the representer theorem arising in Gaussian process regression. The reduced optimization problem has a quadratic loss and nonlinear constraints, and it is in turn solved with a variant of the Gauss-Newton method. The resulting algorithm (a) can be interpreted as solving successive linearizations of the nonlinear PDE, and (b) is found in practice to converge in a small number (two to ten) of iterations in experiments conducted on a range of PDEs. For IPs, while the traditional approach has been to iterate between the identifications of parameters in the PDE and the numerical approximation of its solution, our algorithm tackles both simultaneously. Experiments on nonlinear elliptic PDEs, Burgers' equation, a regularized Eikonal equation, and an IP for permeability identification in Darcy flow illustrate the efficacy and scope of our framework.