Adaptive Projected Residual Networks for Learning Parametric Maps from Sparse Data

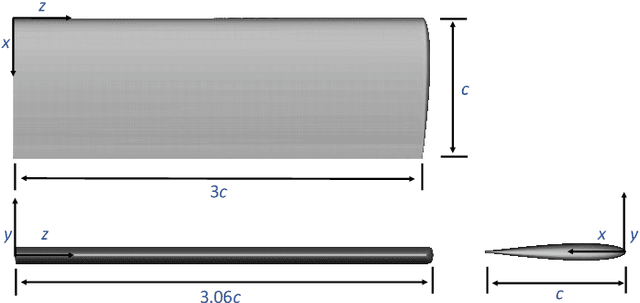
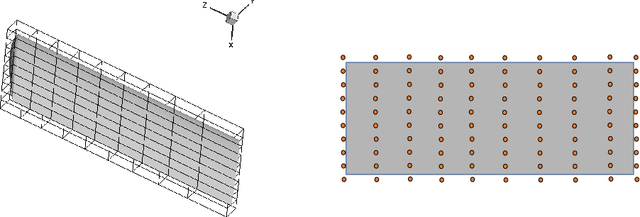
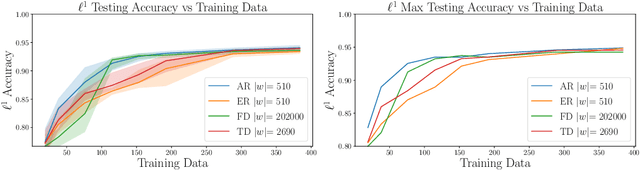
We present a parsimonious surrogate framework for learning high dimensional parametric maps from limited training data. The need for parametric surrogates arises in many applications that require repeated queries of complex computational models. These applications include such "outer-loop" problems as Bayesian inverse problems, optimal experimental design, and optimal design and control under uncertainty, as well as real time inference and control problems. Many high dimensional parametric mappings admit low dimensional structure, which can be exploited by mapping-informed reduced bases of the inputs and outputs. Exploiting this property, we develop a framework for learning low dimensional approximations of such maps by adaptively constructing ResNet approximations between reduced bases of their inputs and output. Motivated by recent approximation theory for ResNets as discretizations of control flows, we prove a universal approximation property of our proposed adaptive projected ResNet framework, which motivates a related iterative algorithm for the ResNet construction. This strategy represents a confluence of the approximation theory and the algorithm since both make use of sequentially minimizing flows. In numerical examples we show that these parsimonious, mapping-informed architectures are able to achieve remarkably high accuracy given few training data, making them a desirable surrogate strategy to be implemented for minimal computational investment in training data generation.

Reduced operator inference for nonlinear partial differential equations

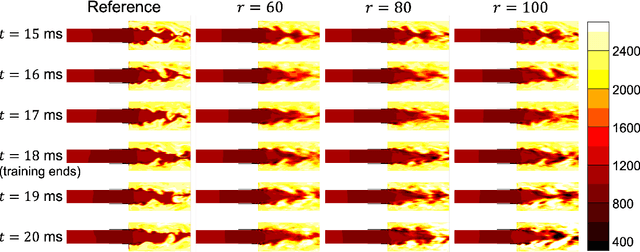
We present a new scientific machine learning method that learns from data a computationally inexpensive surrogate model for predicting the evolution of a system governed by a time-dependent nonlinear partial differential equation (PDE), an enabling technology for many computational algorithms used in engineering settings. Our formulation generalizes to the PDE setting the Operator Inference method previously developed in [B. Peherstorfer and K. Willcox, Data-driven operator inference for non-intrusive projection-based model reduction, Computer Methods in Applied Mechanics and Engineering, 306 (2016)] for systems governed by ordinary differential equations. The method brings together two main elements. First, ideas from projection-based model reduction are used to explicitly parametrize the learned model by low-dimensional polynomial operators which reflect the known form of the governing PDE. Second, supervised machine learning tools are used to infer from data the reduced operators of this physics-informed parametrization. For systems whose governing PDEs contain more general (non-polynomial) nonlinearities, the learned model performance can be improved through the use of lifting variable transformations, which expose polynomial structure in the PDE. The proposed method is demonstrated on a three-dimensional combustion simulation with over 18 million degrees of freedom, for which the learned reduced models achieve accurate predictions with a dimension reduction of six orders of magnitude and model runtime reduction of 5-6 orders of magnitude.

Operator inference for non-intrusive model reduction of systems with non-polynomial nonlinear terms

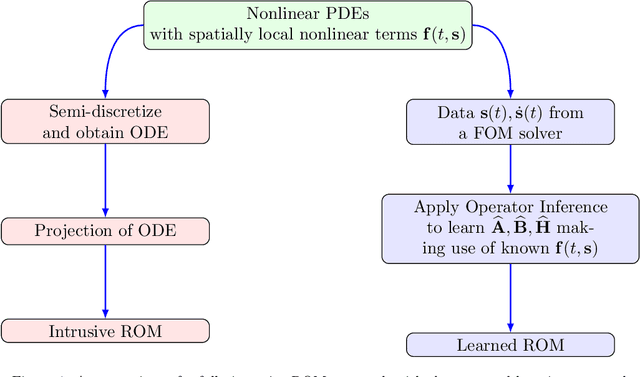
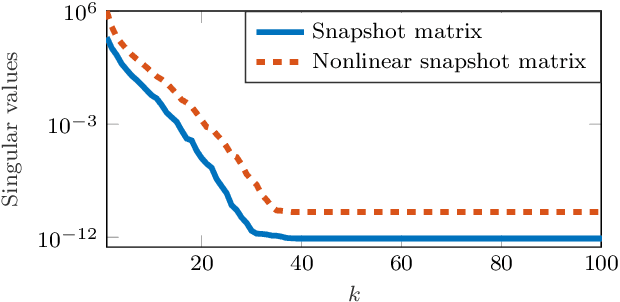
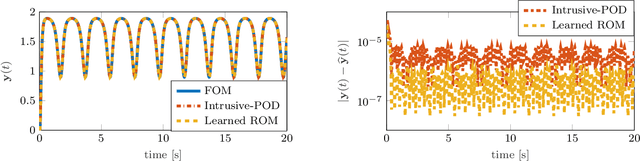
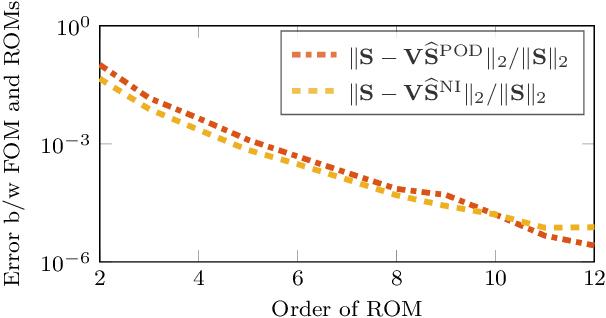
This work presents a non-intrusive model reduction method to learn low-dimensional models of dynamical systems with non-polynomial nonlinear terms that are spatially local and that are given in analytic form. In contrast to state-of-the-art model reduction methods that are intrusive and thus require full knowledge of the governing equations and the operators of a full model of the discretized dynamical system, the proposed approach requires only the non-polynomial terms in analytic form and learns the rest of the dynamics from snapshots computed with a potentially black-box full-model solver. The proposed method learns operators for the linear and polynomially nonlinear dynamics via a least-squares problem, where the given non-polynomial terms are incorporated in the right-hand side. The least-squares problem is linear and thus can be solved efficiently in practice. The proposed method is demonstrated on three problems governed by partial differential equations, namely the diffusion-reaction Chafee-Infante model, a tubular reactor model for reactive flows, and a batch-chromatography model that describes a chemical separation process. The numerical results provide evidence that the proposed approach learns reduced models that achieve comparable accuracy as models constructed with state-of-the-art intrusive model reduction methods that require full knowledge of the governing equations.

Lift & Learn: Physics-informed machine learning for large-scale nonlinear dynamical systems

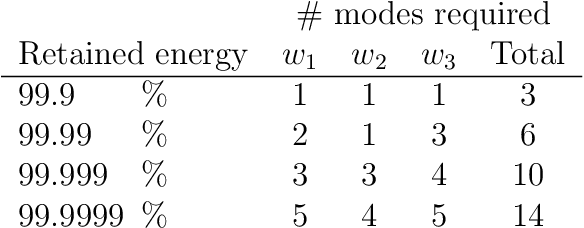
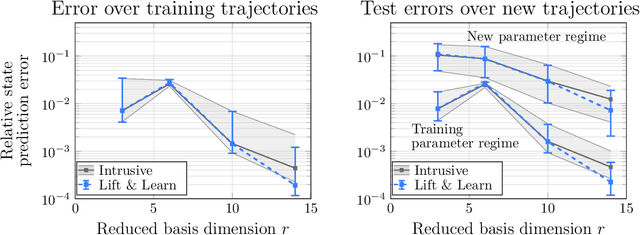
We present Lift & Learn, a physics-informed method for learning low-dimensional models for large-scale dynamical systems. The method exploits knowledge of a system's governing equations to identify a coordinate transformation in which the system dynamics have quadratic structure. This transformation is called a lifting map because it often adds auxiliary variables to the system state. The lifting map is applied to data obtained by evaluating a model for the original nonlinear system. This lifted data is projected onto its leading principal components, and low-dimensional linear and quadratic matrix operators are fit to the lifted reduced data using a least-squares operator inference procedure. Analysis of our method shows that the Lift & Learn models are able to capture the system physics in the lifted coordinates at least as accurately as traditional intrusive model reduction approaches. This preservation of system physics makes the Lift & Learn models robust to changes in inputs. Numerical experiments on the FitzHugh-Nagumo neuron activation model and the compressible Euler equations demonstrate the generalizability of our model.

Learning physics-based reduced-order models for a single-injector combustion process

This paper presents a physics-based data-driven method to learn predictive reduced-order models (ROMs) from high-fidelity simulations, and illustrates it in the challenging context of a single-injector combustion process. The method combines the perspectives of model reduction and machine learning. Model reduction brings in the physics of the problem, constraining the ROM predictions to lie on a subspace defined by the governing equations. This is achieved by defining the ROM in proper orthogonal decomposition (POD) coordinates, which embed the rich physics information contained in solution snapshots of a high-fidelity computational fluid dynamics (CFD) model. The machine learning perspective brings the flexibility to use transformed physical variables to define the POD basis. This is in contrast to traditional model reduction approaches that are constrained to use the physical variables of the high-fidelity code. Combining the two perspectives, the approach identifies a set of transformed physical variables that expose quadratic structure in the combustion governing equations and learns a quadratic ROM from transformed snapshot data. This learning does not require access to the high-fidelity model implementation. Numerical experiments show that the ROM accurately predicts temperature, pressure, velocity, species concentrations, and the limit-cycle amplitude, with speedups of more than five orders of magnitude over high-fidelity models. Moreover, ROM-predicted pressure traces accurately match the phase of the pressure signal and yield good approximations of the limit-cycle amplitude.