Multifidelity linear regression for scientific machine learning from scarce data

Machine learning (ML) methods, which fit to data the parameters of a given parameterized model class, have garnered significant interest as potential methods for learning surrogate models for complex engineering systems for which traditional simulation is expensive. However, in many scientific and engineering settings, generating high-fidelity data on which to train ML models is expensive, and the available budget for generating training data is limited. ML models trained on the resulting scarce high-fidelity data have high variance and are sensitive to vagaries of the training data set. We propose a new multifidelity training approach for scientific machine learning that exploits the scientific context where data of varying fidelities and costs are available; for example high-fidelity data may be generated by an expensive fully resolved physics simulation whereas lower-fidelity data may arise from a cheaper model based on simplifying assumptions. We use the multifidelity data to define new multifidelity Monte Carlo estimators for the unknown parameters of linear regression models, and provide theoretical analyses that guarantee the approach's accuracy and improved robustness to small training budgets. Numerical results verify the theoretical analysis and demonstrate that multifidelity learned models trained on scarce high-fidelity data and additional low-fidelity data achieve order-of-magnitude lower model variance than standard models trained on only high-fidelity data of comparable cost. This illustrates that in the scarce data regime, our multifidelity training strategy yields models with lower expected error than standard training approaches.

Energy-Preserving Reduced Operator Inference for Efficient Design and Control

Many-query computations, in which a computational model for an engineering system must be evaluated many times, are crucial in design and control. For systems governed by partial differential equations (PDEs), typical high-fidelity numerical models are high-dimensional and too computationally expensive for the many-query setting. Thus, efficient surrogate models are required to enable low-cost computations in design and control. This work presents a physics-preserving reduced model learning approach that targets PDEs whose quadratic operators preserve energy, such as those arising in governing equations in many fluids problems. The approach is based on the Operator Inference method, which fits reduced model operators to state snapshot and time derivative data in a least-squares sense. However, Operator Inference does not generally learn a reduced quadratic operator with the energy-preserving property of the original PDE. Thus, we propose a new energy-preserving Operator Inference (EP-OpInf) approach, which imposes this structure on the learned reduced model via constrained optimization. Numerical results using the viscous Burgers' and Kuramoto-Sivashinksy equation (KSE) demonstrate that EP-OpInf learns efficient and accurate reduced models that retain this energy-preserving structure.

Reduced operator inference for nonlinear partial differential equations

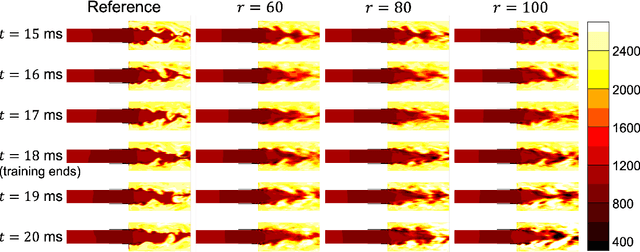
We present a new scientific machine learning method that learns from data a computationally inexpensive surrogate model for predicting the evolution of a system governed by a time-dependent nonlinear partial differential equation (PDE), an enabling technology for many computational algorithms used in engineering settings. Our formulation generalizes to the PDE setting the Operator Inference method previously developed in [B. Peherstorfer and K. Willcox, Data-driven operator inference for non-intrusive projection-based model reduction, Computer Methods in Applied Mechanics and Engineering, 306 (2016)] for systems governed by ordinary differential equations. The method brings together two main elements. First, ideas from projection-based model reduction are used to explicitly parametrize the learned model by low-dimensional polynomial operators which reflect the known form of the governing PDE. Second, supervised machine learning tools are used to infer from data the reduced operators of this physics-informed parametrization. For systems whose governing PDEs contain more general (non-polynomial) nonlinearities, the learned model performance can be improved through the use of lifting variable transformations, which expose polynomial structure in the PDE. The proposed method is demonstrated on a three-dimensional combustion simulation with over 18 million degrees of freedom, for which the learned reduced models achieve accurate predictions with a dimension reduction of six orders of magnitude and model runtime reduction of 5-6 orders of magnitude.

Lift & Learn: Physics-informed machine learning for large-scale nonlinear dynamical systems

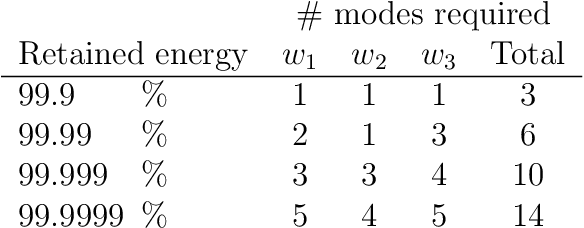
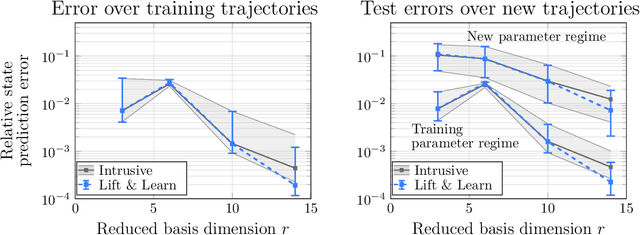
We present Lift & Learn, a physics-informed method for learning low-dimensional models for large-scale dynamical systems. The method exploits knowledge of a system's governing equations to identify a coordinate transformation in which the system dynamics have quadratic structure. This transformation is called a lifting map because it often adds auxiliary variables to the system state. The lifting map is applied to data obtained by evaluating a model for the original nonlinear system. This lifted data is projected onto its leading principal components, and low-dimensional linear and quadratic matrix operators are fit to the lifted reduced data using a least-squares operator inference procedure. Analysis of our method shows that the Lift & Learn models are able to capture the system physics in the lifted coordinates at least as accurately as traditional intrusive model reduction approaches. This preservation of system physics makes the Lift & Learn models robust to changes in inputs. Numerical experiments on the FitzHugh-Nagumo neuron activation model and the compressible Euler equations demonstrate the generalizability of our model.