mfEGRA: Multifidelity Efficient Global Reliability Analysis

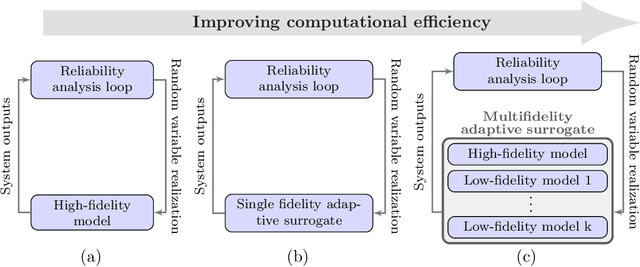
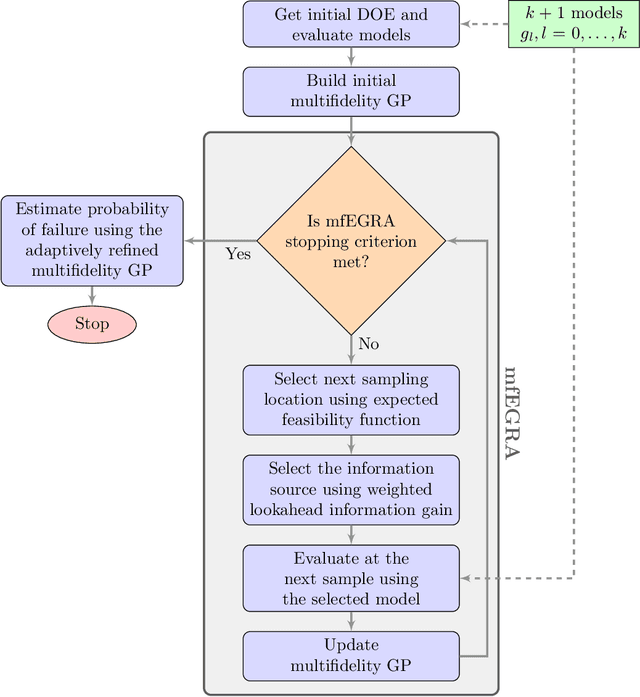
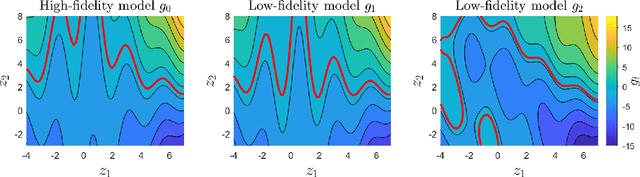
This paper develops mfEGRA, a multifidelity active learning method using data-driven adaptively refined surrogates for failure boundary location in reliability analysis. This work addresses the issue of prohibitive cost of reliability analysis using Monte Carlo sampling for expensive-to-evaluate high-fidelity models by using cheaper-to-evaluate approximations of the high-fidelity model. The method builds on the Efficient Global Reliability Analysis (EGRA) method, which is a surrogate-based method that uses adaptive sampling for refining Gaussian process surrogates for failure boundary location using a single fidelity model. Our method introduces a two-stage adaptive sampling criterion that uses a multifidelity Gaussian process surrogate to leverage multiple information sources with different fidelities. The method combines expected feasibility criterion from EGRA with one-step lookahead information gain to refine the surrogate around the failure boundary. The computational savings from mfEGRA depends on the discrepancy between the different models, and the relative cost of evaluating the different models as compared to the high-fidelity model. We show that accurate estimation of reliability using mfEGRA leads to computational savings of around 50% for an analytical multimodal test problem and 24% for an acoustic horn problem, when compared to single fidelity EGRA.

Contour location via entropy reduction leveraging multiple information sources

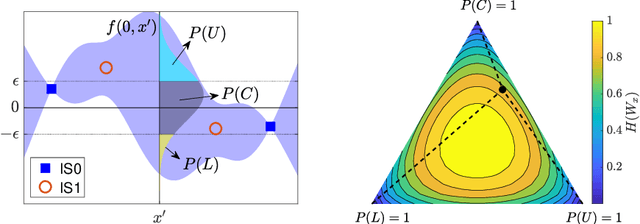
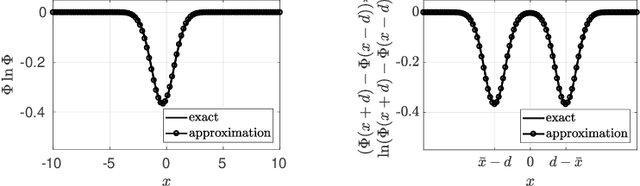
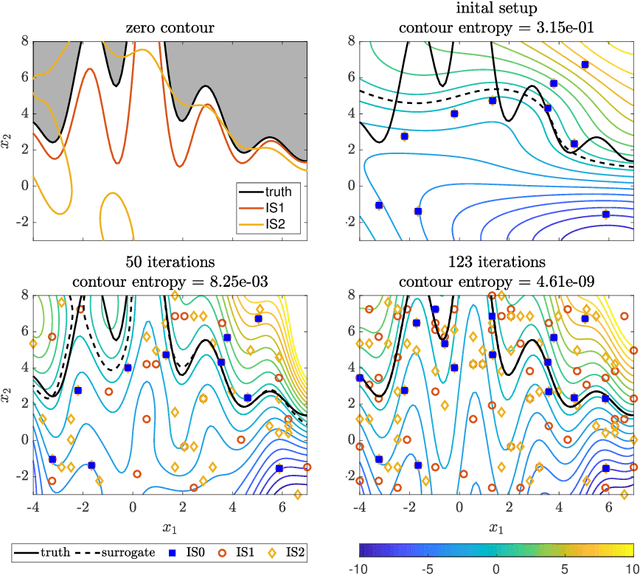
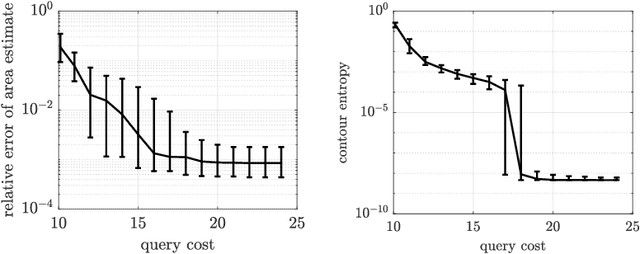
We introduce an algorithm to locate contours of functions that are expensive to evaluate. The problem of locating contours arises in many applications, including classification, constrained optimization, and performance analysis of mechanical and dynamical systems (reliability, probability of failure, stability, etc.). Our algorithm locates contours using information from multiple sources, which are available in the form of relatively inexpensive, biased, and possibly noisy approximations to the original function. Considering multiple information sources can lead to significant cost savings. We also introduce the concept of contour entropy, a formal measure of uncertainty about the location of the zero contour of a function approximated by a statistical surrogate model. Our algorithm locates contours efficiently by maximizing the reduction of contour entropy per unit cost.