Distributed computing for physics-based data-driven reduced modeling at scale: Application to a rotating detonation rocket engine

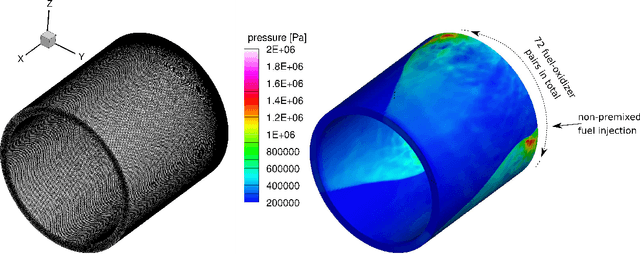
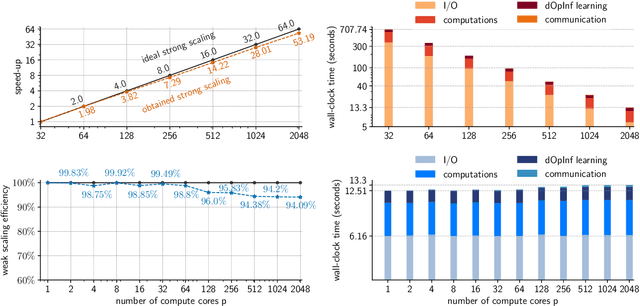
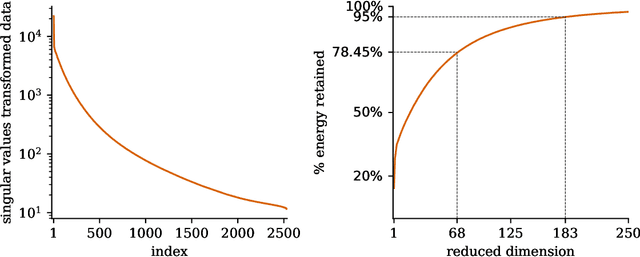
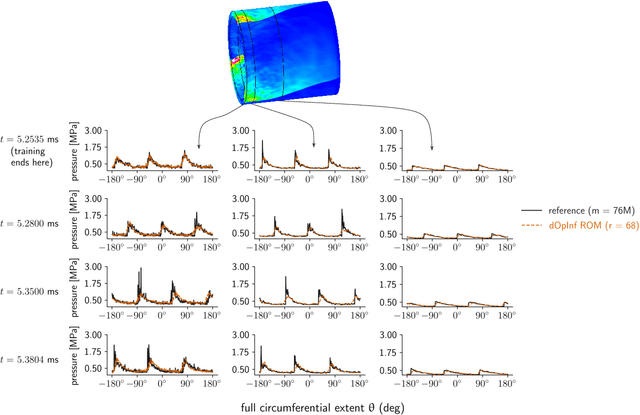
High-performance computing (HPC) has revolutionized our ability to perform detailed simulations of complex real-world processes. A prominent contemporary example is from aerospace propulsion, where HPC is used for rotating detonation rocket engine (RDRE) simulations in support of the design of next-generation rocket engines; however, these simulations take millions of core hours even on powerful supercomputers, which makes them impractical for engineering tasks like design exploration and risk assessment. Reduced-order models (ROMs) address this limitation by constructing computationally cheap yet sufficiently accurate approximations that serve as surrogates for the high-fidelity model. This paper contributes a new distributed algorithm that achieves fast and scalable construction of predictive physics-based ROMs trained from sparse datasets of extremely large state dimension. The algorithm learns structured physics-based ROMs that approximate the dynamical systems underlying those datasets. This enables model reduction for problems at a scale and complexity that exceeds the capabilities of existing approaches. We demonstrate our algorithm's scalability using up to $2,048$ cores on the Frontera supercomputer at the Texas Advanced Computing Center. We focus on a real-world three-dimensional RDRE for which one millisecond of simulated physical time requires one million core hours on a supercomputer. Using a training dataset of $2,536$ snapshots each of state dimension $76$ million, our distributed algorithm enables the construction of a predictive data-driven reduced model in just $13$ seconds on $2,048$ cores on Frontera.

A digital twin framework for civil engineering structures

The digital twin concept represents an appealing opportunity to advance condition-based and predictive maintenance paradigms for civil engineering systems, thus allowing reduced lifecycle costs, increased system safety, and increased system availability. This work proposes a predictive digital twin approach to the health monitoring, maintenance, and management planning of civil engineering structures. The asset-twin coupled dynamical system is encoded employing a probabilistic graphical model, which allows all relevant sources of uncertainty to be taken into account. In particular, the time-repeating observations-to-decisions flow is modeled using a dynamic Bayesian network. Real-time structural health diagnostics are provided by assimilating sensed data with deep learning models. The digital twin state is continually updated in a sequential Bayesian inference fashion. This is then exploited to inform the optimal planning of maintenance and management actions within a dynamic decision-making framework. A preliminary offline phase involves the population of training datasets through a reduced-order numerical model and the computation of a health-dependent control policy. The strategy is assessed on two synthetic case studies, involving a cantilever beam and a railway bridge, demonstrating the dynamic decision-making capabilities of health-aware digital twins.

A Probabilistic Graphical Model Foundation for Enabling Predictive Digital Twins at Scale

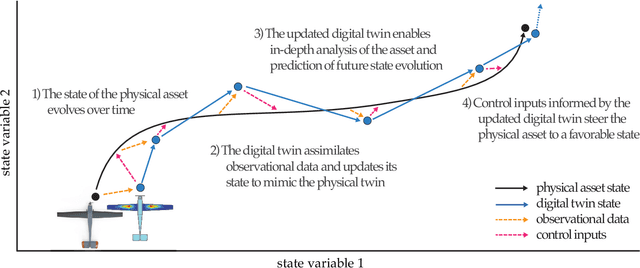
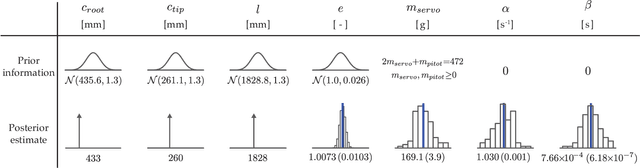
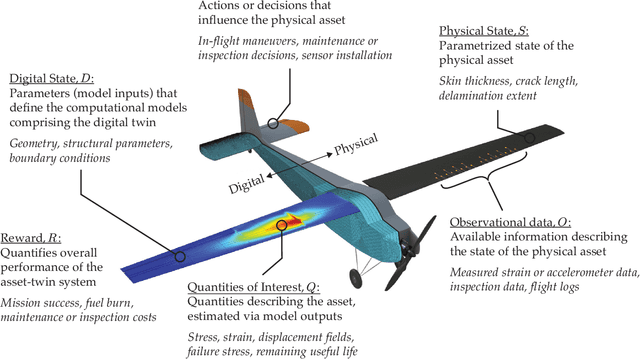
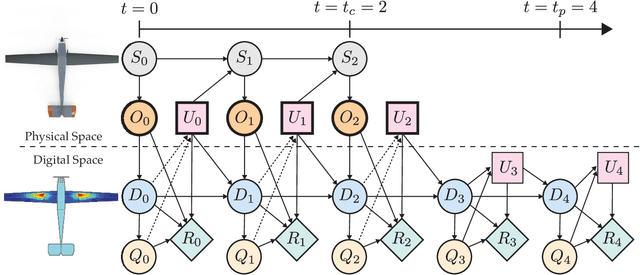
A unifying mathematical formulation is needed to move from one-off digital twins built through custom implementations to robust digital twin implementations at scale. This work proposes a probabilistic graphical model as a formal mathematical representation of a digital twin and its associated physical asset. We create an abstraction of the asset-twin system as a set of coupled dynamical systems, evolving over time through their respective state-spaces and interacting via observed data and control inputs. The formal definition of this coupled system as a probabilistic graphical model enables us to draw upon well-established theory and methods from Bayesian statistics, dynamical systems, and control theory. The declarative and general nature of the proposed digital twin model make it rigorous yet flexible, enabling its application at scale in a diverse range of application areas. We demonstrate how the model is instantiated as a Bayesian network to create a structural digital twin of an unmanned aerial vehicle. The graphical model foundation ensures that the digital twin creation and updating process is principled, repeatable, and able to scale to the calibration of an entire fleet of digital twins.

From Physics-Based Models to Predictive Digital Twins via Interpretable Machine Learning

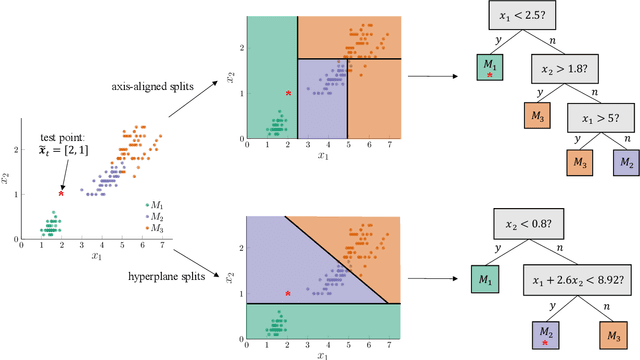
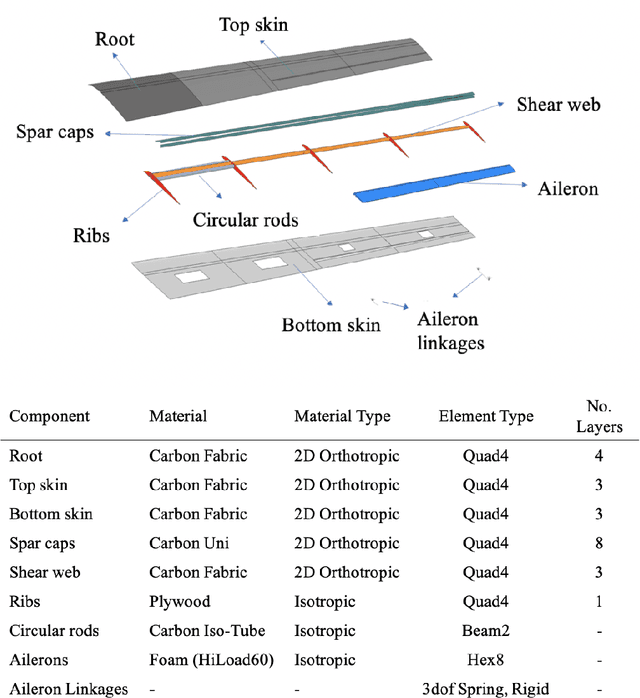
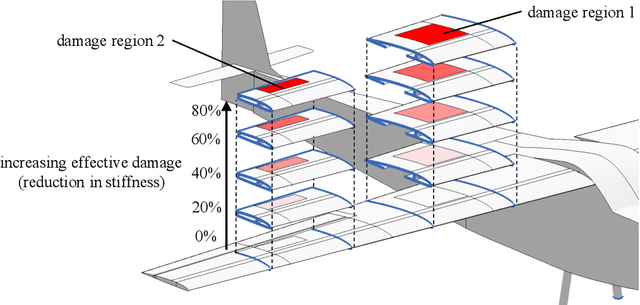
This work develops a methodology for creating a data-driven digital twin from a library of physics-based models representing various asset states. The digital twin is updated using interpretable machine learning. Specifically, we use optimal trees---a recently developed scalable machine learning method---to train an interpretable data-driven classifier. Training data for the classifier are generated offline using simulated scenarios solved by the library of physics-based models. These data can be further augmented using experimental or other historical data. In operation, the classifier uses observational data from the asset to infer which physics-based models in the model library are the best candidates for the updated digital twin. The approach is demonstrated through the development of a structural digital twin for a 12ft wingspan unmanned aerial vehicle. This digital twin is built from a library of reduced-order models of the vehicle in a range of structural states. The data-driven digital twin dynamically updates in response to structural damage or degradation and enables the aircraft to replan a safe mission accordingly. Within this context, we study the performance of the optimal tree classifiers and demonstrate how their interpretability enables explainable structural assessments from sparse sensor measurements, and also informs optimal sensor placement.

mfEGRA: Multifidelity Efficient Global Reliability Analysis

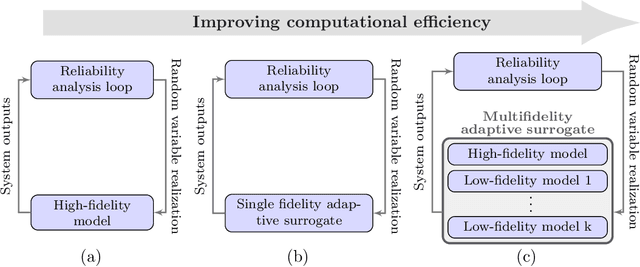
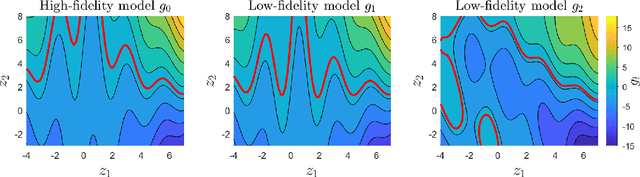
This paper develops mfEGRA, a multifidelity active learning method using data-driven adaptively refined surrogates for failure boundary location in reliability analysis. This work addresses the issue of prohibitive cost of reliability analysis using Monte Carlo sampling for expensive-to-evaluate high-fidelity models by using cheaper-to-evaluate approximations of the high-fidelity model. The method builds on the Efficient Global Reliability Analysis (EGRA) method, which is a surrogate-based method that uses adaptive sampling for refining Gaussian process surrogates for failure boundary location using a single fidelity model. Our method introduces a two-stage adaptive sampling criterion that uses a multifidelity Gaussian process surrogate to leverage multiple information sources with different fidelities. The method combines expected feasibility criterion from EGRA with one-step lookahead information gain to refine the surrogate around the failure boundary. The computational savings from mfEGRA depends on the discrepancy between the different models, and the relative cost of evaluating the different models as compared to the high-fidelity model. We show that accurate estimation of reliability using mfEGRA leads to computational savings of around 50% for an analytical multimodal test problem and 24% for an acoustic horn problem, when compared to single fidelity EGRA.

Contour location via entropy reduction leveraging multiple information sources

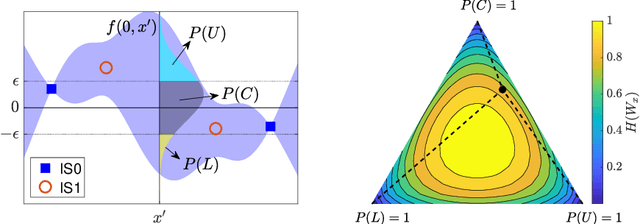
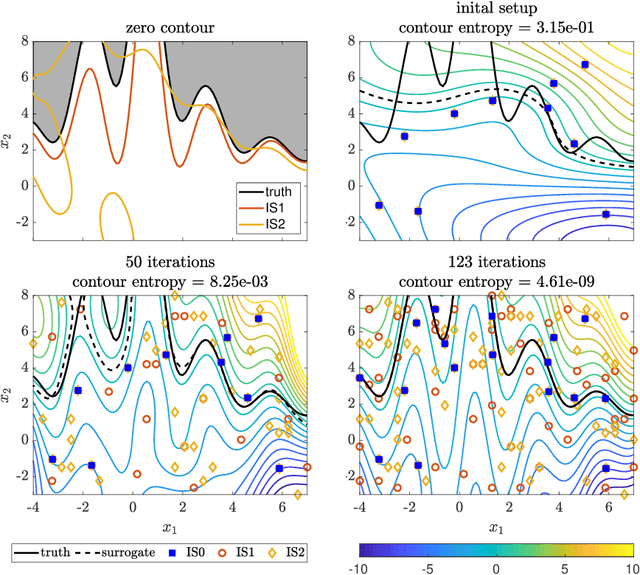
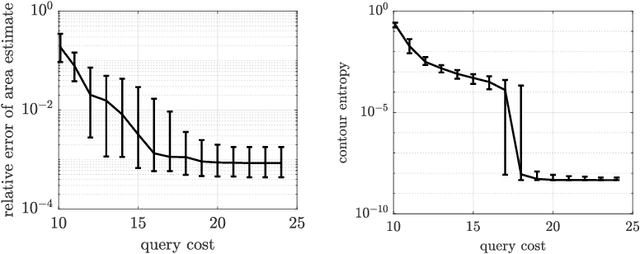
We introduce an algorithm to locate contours of functions that are expensive to evaluate. The problem of locating contours arises in many applications, including classification, constrained optimization, and performance analysis of mechanical and dynamical systems (reliability, probability of failure, stability, etc.). Our algorithm locates contours using information from multiple sources, which are available in the form of relatively inexpensive, biased, and possibly noisy approximations to the original function. Considering multiple information sources can lead to significant cost savings. We also introduce the concept of contour entropy, a formal measure of uncertainty about the location of the zero contour of a function approximated by a statistical surrogate model. Our algorithm locates contours efficiently by maximizing the reduction of contour entropy per unit cost.

Should You Derive, Or Let the Data Drive? An Optimization Framework for Hybrid First-Principles Data-Driven Modeling

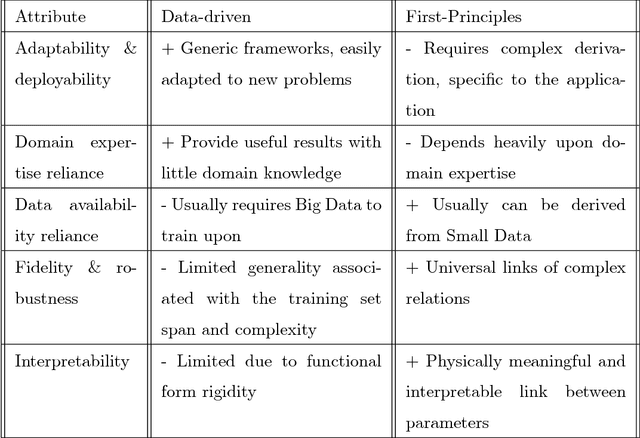
Mathematical models are used extensively for diverse tasks including analysis, optimization, and decision making. Frequently, those models are principled but imperfect representations of reality. This is either due to incomplete physical description of the underlying phenomenon (simplified governing equations, defective boundary conditions, etc.), or due to numerical approximations (discretization, linearization, round-off error, etc.). Model misspecification can lead to erroneous model predictions, and respectively suboptimal decisions associated with the intended end-goal task. To mitigate this effect, one can amend the available model using limited data produced by experiments or higher fidelity models. A large body of research has focused on estimating explicit model parameters. This work takes a different perspective and targets the construction of a correction model operator with implicit attributes. We investigate the case where the end-goal is inversion and illustrate how appropriate choices of properties imposed upon the correction and corrected operator lead to improved end-goal insights.