A digital twin framework for civil engineering structures

The digital twin concept represents an appealing opportunity to advance condition-based and predictive maintenance paradigms for civil engineering systems, thus allowing reduced lifecycle costs, increased system safety, and increased system availability. This work proposes a predictive digital twin approach to the health monitoring, maintenance, and management planning of civil engineering structures. The asset-twin coupled dynamical system is encoded employing a probabilistic graphical model, which allows all relevant sources of uncertainty to be taken into account. In particular, the time-repeating observations-to-decisions flow is modeled using a dynamic Bayesian network. Real-time structural health diagnostics are provided by assimilating sensed data with deep learning models. The digital twin state is continually updated in a sequential Bayesian inference fashion. This is then exploited to inform the optimal planning of maintenance and management actions within a dynamic decision-making framework. A preliminary offline phase involves the population of training datasets through a reduced-order numerical model and the computation of a health-dependent control policy. The strategy is assessed on two synthetic case studies, involving a cantilever beam and a railway bridge, demonstrating the dynamic decision-making capabilities of health-aware digital twins.

A DeepONet Multi-Fidelity Approach for Residual Learning in Reduced Order Modeling

In the present work, we introduce a novel approach to enhance the precision of reduced order models by exploiting a multi-fidelity perspective and DeepONets. Reduced models provide a real-time numerical approximation by simplifying the original model. The error introduced by such operation is usually neglected and sacrificed in order to reach a fast computation. We propose to couple the model reduction to a machine learning residual learning, such that the above-mentioned error can be learnt by a neural network and inferred for new predictions. We emphasize that the framework maximizes the exploitation of the high-fidelity information, using it for building the reduced order model and for learning the residual. In this work we explore the integration of proper orthogonal decomposition (POD), and gappy POD for sensors data, with the recent DeepONet architecture. Numerical investigations for a parametric benchmark function and a nonlinear parametric Navier-Stokes problem are presented.

A local approach to parameter space reduction for regression and classification tasks

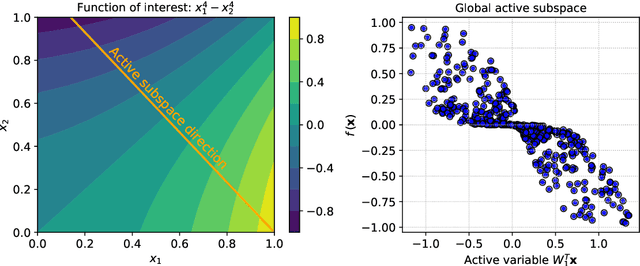
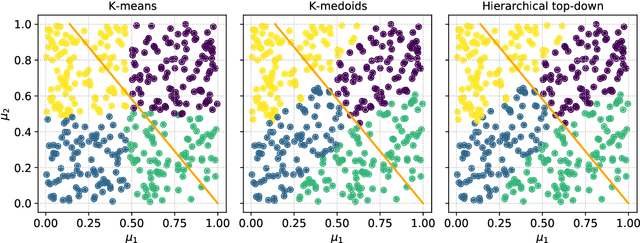
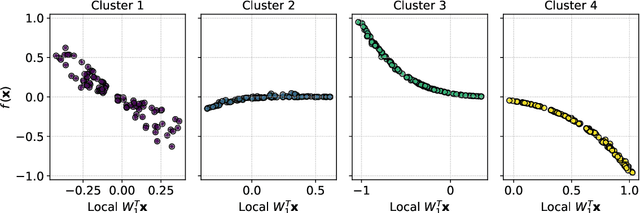
Frequently, the parameter space, chosen for shape design or other applications that involve the definition of a surrogate model, present subdomains where the objective function of interest is highly regular or well behaved. So, it could be approximated more accurately if restricted to those subdomains and studied separately. The drawback of this approach is the possible scarcity of data in some applications, but in those, where a quantity of data, moderately abundant considering the parameter space dimension and the complexity of the objective function, is available, partitioned or local studies are beneficial. In this work we propose a new method called local active subspaces (LAS), which explores the synergies of active subspaces with supervised clustering techniques in order to perform a more efficient dimension reduction in the parameter space for the design of accurate response surfaces. We also developed a procedure to exploit the local active subspace information for classification tasks. Using this technique as a preprocessing step onto the parameter space, or output space in case of vectorial outputs, brings remarkable results for the purpose of surrogate modelling.

Multi-fidelity data fusion for the approximation of scalar functions with low intrinsic dimensionality through active subspaces

Gaussian processes are employed for non-parametric regression in a Bayesian setting. They generalize linear regression, embedding the inputs in a latent manifold inside an infinite-dimensional reproducing kernel Hilbert space. We can augment the inputs with the observations of low-fidelity models in order to learn a more expressive latent manifold and thus increment the model's accuracy. This can be realized recursively with a chain of Gaussian processes with incrementally higher fidelity. We would like to extend these multi-fidelity model realizations to case studies affected by a high-dimensional input space but with low intrinsic dimensionality. In this cases physical supported or purely numerical low-order models are still affected by the curse of dimensionality when queried for responses. When the model's gradient information is provided, the presence of an active subspace can be exploited to design low-fidelity response surfaces and thus enable Gaussian process multi-fidelity regression, without the need to perform new simulations. This is particularly useful in the case of data scarcity. In this work we present a multi-fidelity approach involving active subspaces and we test it on two different high-dimensional benchmarks.