A local approach to parameter space reduction for regression and classification tasks
Paper and Code
Jul 22, 2021
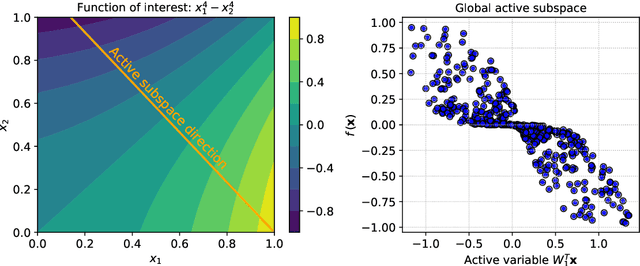
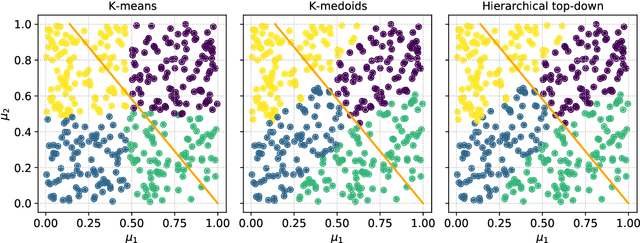
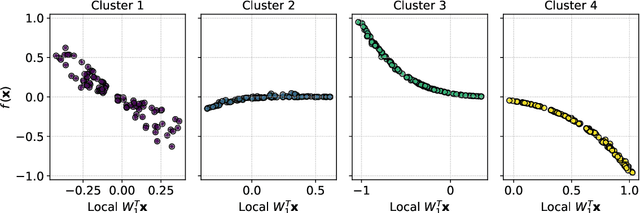
Frequently, the parameter space, chosen for shape design or other applications that involve the definition of a surrogate model, present subdomains where the objective function of interest is highly regular or well behaved. So, it could be approximated more accurately if restricted to those subdomains and studied separately. The drawback of this approach is the possible scarcity of data in some applications, but in those, where a quantity of data, moderately abundant considering the parameter space dimension and the complexity of the objective function, is available, partitioned or local studies are beneficial. In this work we propose a new method called local active subspaces (LAS), which explores the synergies of active subspaces with supervised clustering techniques in order to perform a more efficient dimension reduction in the parameter space for the design of accurate response surfaces. We also developed a procedure to exploit the local active subspace information for classification tasks. Using this technique as a preprocessing step onto the parameter space, or output space in case of vectorial outputs, brings remarkable results for the purpose of surrogate modelling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge