Non-linear manifold ROM with Convolutional Autoencoders and Reduced Over-Collocation method

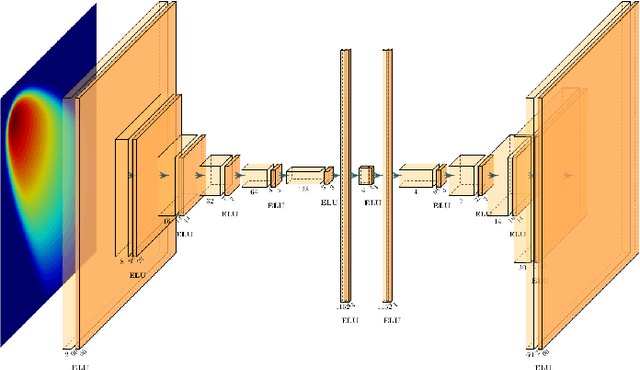
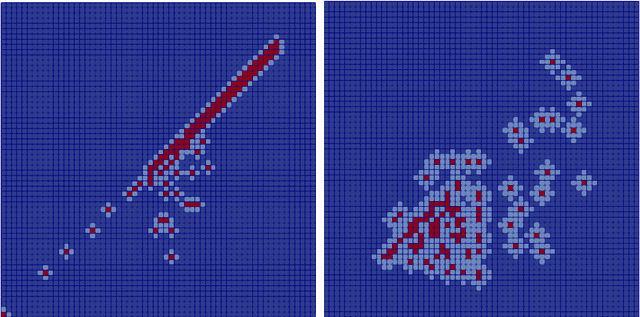
Non-affine parametric dependencies, nonlinearities and advection-dominated regimes of the model of interest can result in a slow Kolmogorov n-width decay, which precludes the realization of efficient reduced-order models based on linear subspace approximations. Among the possible solutions, there are purely data-driven methods that leverage autoencoders and their variants to learn a latent representation of the dynamical system, and then evolve it in time with another architecture. Despite their success in many applications where standard linear techniques fail, more has to be done to increase the interpretability of the results, especially outside the training range and not in regimes characterized by an abundance of data. Not to mention that none of the knowledge on the physics of the model is exploited during the predictive phase. In order to overcome these weaknesses, we implement the non-linear manifold method introduced by Carlberg et al [37] with hyper-reduction achieved through reduced over-collocation and teacher-student training of a reduced decoder. We test the methodology on a 2d non-linear conservation law and a 2d shallow water models, and compare the results obtained with a purely data-driven method for which the dynamics is evolved in time with a long-short term memory network.

A local approach to parameter space reduction for regression and classification tasks

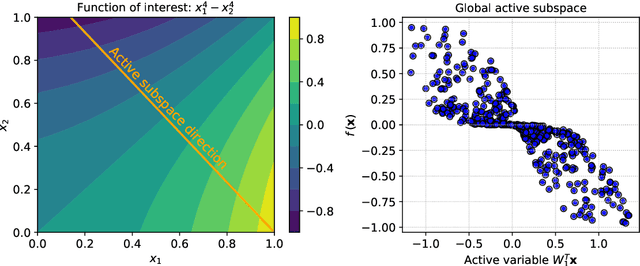
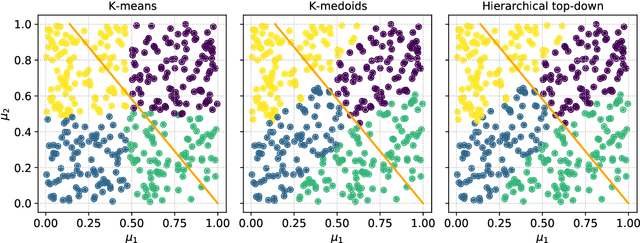
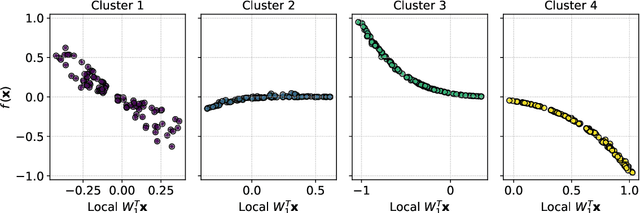
Frequently, the parameter space, chosen for shape design or other applications that involve the definition of a surrogate model, present subdomains where the objective function of interest is highly regular or well behaved. So, it could be approximated more accurately if restricted to those subdomains and studied separately. The drawback of this approach is the possible scarcity of data in some applications, but in those, where a quantity of data, moderately abundant considering the parameter space dimension and the complexity of the objective function, is available, partitioned or local studies are beneficial. In this work we propose a new method called local active subspaces (LAS), which explores the synergies of active subspaces with supervised clustering techniques in order to perform a more efficient dimension reduction in the parameter space for the design of accurate response surfaces. We also developed a procedure to exploit the local active subspace information for classification tasks. Using this technique as a preprocessing step onto the parameter space, or output space in case of vectorial outputs, brings remarkable results for the purpose of surrogate modelling.

Multi-fidelity data fusion for the approximation of scalar functions with low intrinsic dimensionality through active subspaces

Gaussian processes are employed for non-parametric regression in a Bayesian setting. They generalize linear regression, embedding the inputs in a latent manifold inside an infinite-dimensional reproducing kernel Hilbert space. We can augment the inputs with the observations of low-fidelity models in order to learn a more expressive latent manifold and thus increment the model's accuracy. This can be realized recursively with a chain of Gaussian processes with incrementally higher fidelity. We would like to extend these multi-fidelity model realizations to case studies affected by a high-dimensional input space but with low intrinsic dimensionality. In this cases physical supported or purely numerical low-order models are still affected by the curse of dimensionality when queried for responses. When the model's gradient information is provided, the presence of an active subspace can be exploited to design low-fidelity response surfaces and thus enable Gaussian process multi-fidelity regression, without the need to perform new simulations. This is particularly useful in the case of data scarcity. In this work we present a multi-fidelity approach involving active subspaces and we test it on two different high-dimensional benchmarks.