A Predictive Surrogate Model for Heat Transfer of an Impinging Jet on a Concave Surface

This paper aims to comprehensively investigate the efficacy of various Model Order Reduction (MOR) and deep learning techniques in predicting heat transfer in a pulsed jet impinging on a concave surface. Expanding on the previous experimental and numerical research involving pulsed circular jets, this investigation extends to evaluate Predictive Surrogate Models (PSM) for heat transfer across various jet characteristics. To this end, this work introduces two predictive approaches, one employing a Fast Fourier Transformation augmented Artificial Neural Network (FFT-ANN) for predicting the average Nusselt number under constant-frequency scenarios. Moreover, the investigation introduces the Proper Orthogonal Decomposition and Long Short-Term Memory (POD-LSTM) approach for random-frequency impingement jets. The POD-LSTM method proves to be a robust solution for predicting the local heat transfer rate under random-frequency impingement scenarios, capturing both the trend and value of temporal modes. The comparison of these approaches highlights the versatility and efficacy of advanced machine learning techniques in modelling complex heat transfer phenomena.

Deep Reinforcement Learning for the Heat Transfer Control of Pulsating Impinging Jets

This research study explores the applicability of Deep Reinforcement Learning (DRL) for thermal control based on Computational Fluid Dynamics. To accomplish that, the forced convection on a hot plate prone to a pulsating cooling jet with variable velocity has been investigated. We begin with evaluating the efficiency and viability of a vanilla Deep Q-Network (DQN) method for thermal control. Subsequently, a comprehensive comparison between different variants of DRL is conducted. Soft Double and Duel DQN achieved better thermal control performance among all the variants due to their efficient learning and action prioritization capabilities. Results demonstrate that the soft Double DQN outperforms the hard Double DQN. Moreover, soft Double and Duel can maintain the temperature in the desired threshold for more than 98% of the control cycle. These findings demonstrate the promising potential of DRL in effectively addressing thermal control systems.

A two stages Deep Learning Architecture for Model Reduction of Parametric Time-Dependent Problems

Parametric time-dependent systems are of a crucial importance in modeling real phenomena, often characterized by non-linear behaviors too. Those solutions are typically difficult to generalize in a sufficiently wide parameter space while counting on limited computational resources available. As such, we present a general two-stages deep learning framework able to perform that generalization with low computational effort in time. It consists in a separated training of two pipe-lined predictive models. At first, a certain number of independent neural networks are trained with data-sets taken from different subsets of the parameter space. Successively, a second predictive model is specialized to properly combine the first-stage guesses and compute the right predictions. Promising results are obtained applying the framework to incompressible Navier-Stokes equations in a cavity (Rayleigh-Bernard cavity), obtaining a 97% reduction in the computational time comparing with its numerical resolution for a new value of the Grashof number.

A Continuous Convolutional Trainable Filter for Modelling Unstructured Data

Convolutional Neural Network (CNN) is one of the most important architectures in deep learning. The fundamental building block of a CNN is a trainable filter, represented as a discrete grid, used to perform convolution on discrete input data. In this work, we propose a continuous version of a trainable convolutional filter able to work also with unstructured data. This new framework allows exploring CNNs beyond discrete domains, enlarging the usage of this important learning technique for many more complex problems. Our experiments show that the continuous filter can achieve a level of accuracy comparable to the state-of-the-art discrete filter, and that it can be used in current deep learning architectures as a building block to solve problems with unstructured domains as well.

Non-linear manifold ROM with Convolutional Autoencoders and Reduced Over-Collocation method

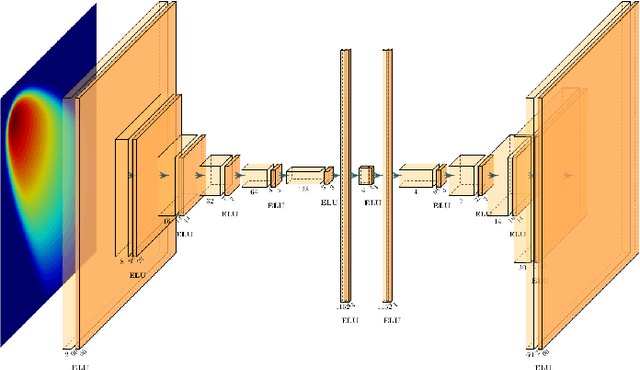
Non-affine parametric dependencies, nonlinearities and advection-dominated regimes of the model of interest can result in a slow Kolmogorov n-width decay, which precludes the realization of efficient reduced-order models based on linear subspace approximations. Among the possible solutions, there are purely data-driven methods that leverage autoencoders and their variants to learn a latent representation of the dynamical system, and then evolve it in time with another architecture. Despite their success in many applications where standard linear techniques fail, more has to be done to increase the interpretability of the results, especially outside the training range and not in regimes characterized by an abundance of data. Not to mention that none of the knowledge on the physics of the model is exploited during the predictive phase. In order to overcome these weaknesses, we implement the non-linear manifold method introduced by Carlberg et al [37] with hyper-reduction achieved through reduced over-collocation and teacher-student training of a reduced decoder. We test the methodology on a 2d non-linear conservation law and a 2d shallow water models, and compare the results obtained with a purely data-driven method for which the dynamics is evolved in time with a long-short term memory network.

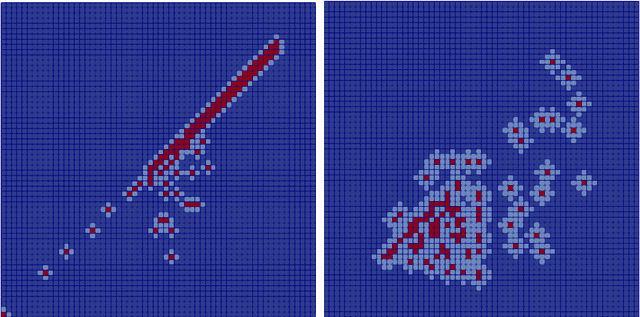
The Neural Network shifted-Proper Orthogonal Decomposition: a Machine Learning Approach for Non-linear Reduction of Hyperbolic Equations

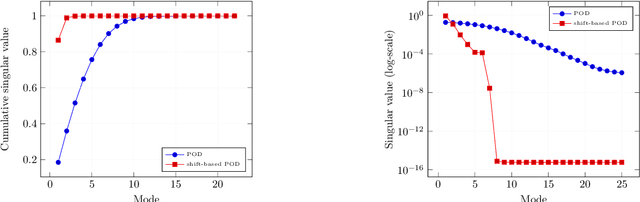
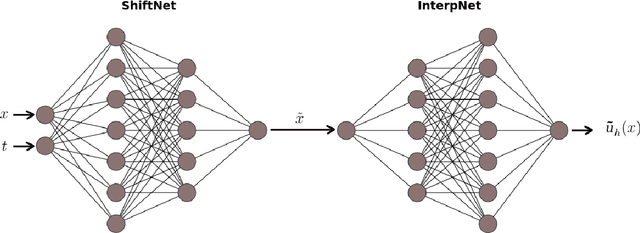
Models with dominant advection always posed a difficult challenge for projection-based reduced order modelling. Many methodologies that have recently been proposed are based on the pre-processing of the full-order solutions to accelerate the Kolmogorov N-width decay thereby obtaining smaller linear subspaces with improved accuracy. These methods however must rely on the knowledge of the characteristic speeds in phase space of the solution, limiting their range of applicability to problems with explicit functional form for the advection field. In this work we approach the problem of automatically detecting the correct pre-processing transformation in a statistical learning framework by implementing a deep-learning architecture. The purely data-driven method allowed us to generalise the existing approaches of linear subspace manipulation to non-linear hyperbolic problems with unknown advection fields. The proposed algorithm has been validated against simple test cases to benchmark its performances and later successfully applied to a multiphase simulation.

Hybrid neural network reduced order modelling for turbulent flows with geometric parameters

Geometrically parametrized Partial Differential Equations are nowadays widely used in many different fields as, for example, shape optimization processes or patient specific surgery studies. The focus of this work is on some advances for this topic, capable of increasing the accuracy with respect to previous approaches while relying on a high cost-benefit ratio performance. The main scope of this paper is the introduction of a new technique mixing up a classical Galerkin-projection approach together with a data-driven method to obtain a versatile and accurate algorithm for the resolution of geometrically parametrized incompressible turbulent Navier-Stokes problems. The effectiveness of this procedure is demonstrated on two different test cases: a classical academic back step problem and a shape deformation Ahmed body application. The results show into details the properties of the architecture we developed while exposing possible future perspectives for this work.