A Continuous Convolutional Trainable Filter for Modelling Unstructured Data

Convolutional Neural Network (CNN) is one of the most important architectures in deep learning. The fundamental building block of a CNN is a trainable filter, represented as a discrete grid, used to perform convolution on discrete input data. In this work, we propose a continuous version of a trainable convolutional filter able to work also with unstructured data. This new framework allows exploring CNNs beyond discrete domains, enlarging the usage of this important learning technique for many more complex problems. Our experiments show that the continuous filter can achieve a level of accuracy comparable to the state-of-the-art discrete filter, and that it can be used in current deep learning architectures as a building block to solve problems with unstructured domains as well.

A Proper Orthogonal Decomposition approach for parameters reduction of Single Shot Detector networks

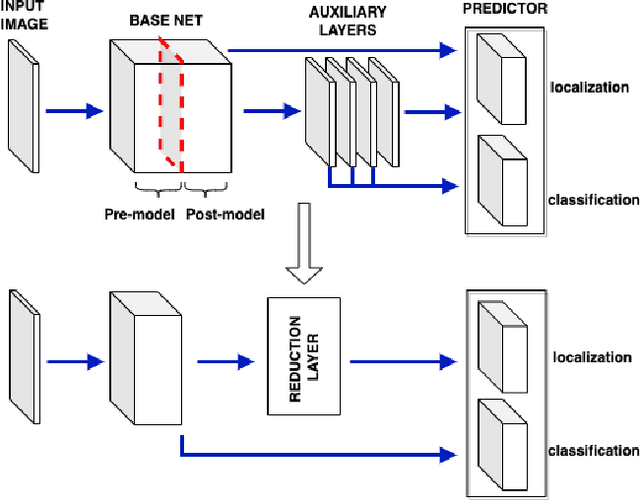
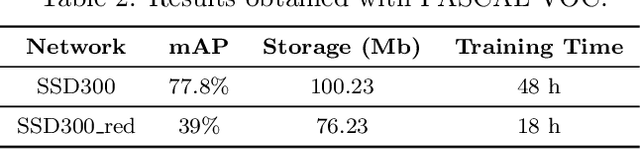
As a major breakthrough in artificial intelligence and deep learning, Convolutional Neural Networks have achieved an impressive success in solving many problems in several fields including computer vision and image processing. Real-time performance, robustness of algorithms and fast training processes remain open problems in these contexts. In addition object recognition and detection are challenging tasks for resource-constrained embedded systems, commonly used in the industrial sector. To overcome these issues, we propose a dimensionality reduction framework based on Proper Orthogonal Decomposition, a classical model order reduction technique, in order to gain a reduction in the number of hyperparameters of the net. We have applied such framework to SSD300 architecture using PASCAL VOC dataset, demonstrating a reduction of the network dimension and a remarkable speedup in the fine-tuning of the network in a transfer learning context.

A Dimensionality Reduction Approach for Convolutional Neural Networks

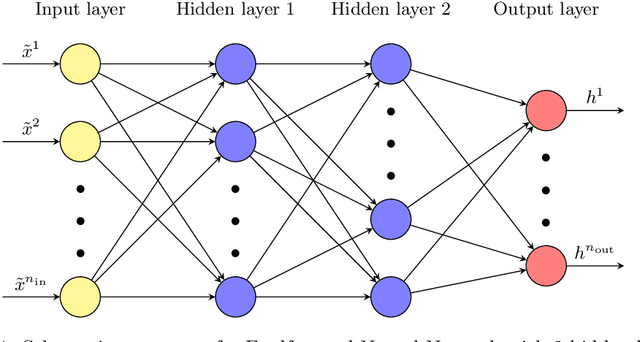
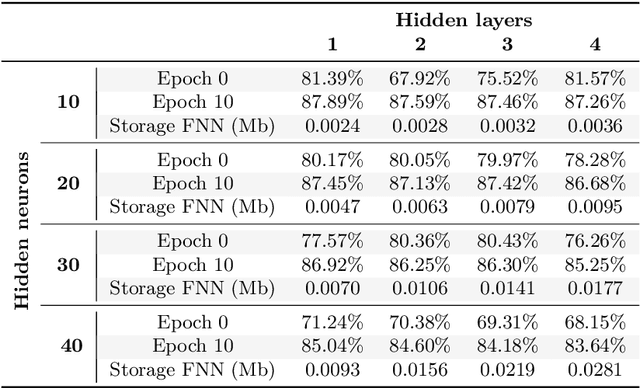
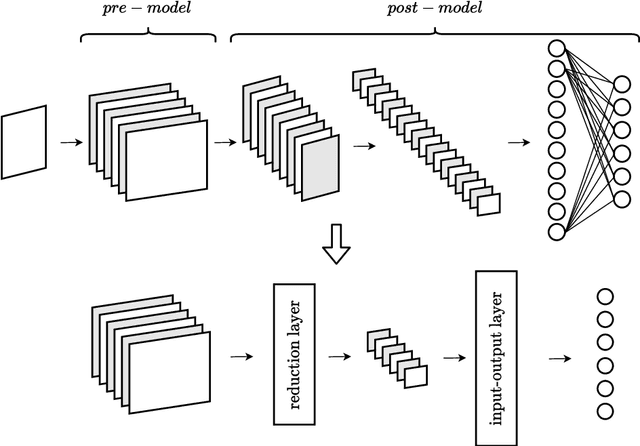
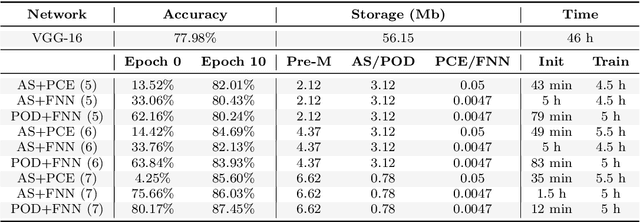
The focus of this paper is the application of classical model order reduction techniques, such as Active Subspaces and Proper Orthogonal Decomposition, to Deep Neural Networks. We propose a generic methodology to reduce the number of layers of a pre-trained network by combining the aforementioned techniques for dimensionality reduction with input-output mappings, such as Polynomial Chaos Expansion and Feedforward Neural Networks. The necessity of compressing the architecture of an existing Convolutional Neural Network is motivated by its application in embedded systems with specific storage constraints. Our experiment shows that the reduced nets obtained can achieve a level of accuracy similar to the original Convolutional Neural Network under examination, while saving in memory allocation.