Generative Adversarial Reduced Order Modelling

In this work, we present GAROM, a new approach for reduced order modelling (ROM) based on generative adversarial networks (GANs). GANs have the potential to learn data distribution and generate more realistic data. While widely applied in many areas of deep learning, little research is done on their application for ROM, i.e. approximating a high-fidelity model with a simpler one. In this work, we combine the GAN and ROM framework, by introducing a data-driven generative adversarial model able to learn solutions to parametric differential equations. The latter is achieved by modelling the discriminator network as an autoencoder, extracting relevant features of the input, and applying a conditioning mechanism to the generator and discriminator networks specifying the differential equation parameters. We show how to apply our methodology for inference, provide experimental evidence of the model generalisation, and perform a convergence study of the method.

A DeepONet Multi-Fidelity Approach for Residual Learning in Reduced Order Modeling

In the present work, we introduce a novel approach to enhance the precision of reduced order models by exploiting a multi-fidelity perspective and DeepONets. Reduced models provide a real-time numerical approximation by simplifying the original model. The error introduced by such operation is usually neglected and sacrificed in order to reach a fast computation. We propose to couple the model reduction to a machine learning residual learning, such that the above-mentioned error can be learnt by a neural network and inferred for new predictions. We emphasize that the framework maximizes the exploitation of the high-fidelity information, using it for building the reduced order model and for learning the residual. In this work we explore the integration of proper orthogonal decomposition (POD), and gappy POD for sensors data, with the recent DeepONet architecture. Numerical investigations for a parametric benchmark function and a nonlinear parametric Navier-Stokes problem are presented.

Towards a machine learning pipeline in reduced order modelling for inverse problems: neural networks for boundary parametrization, dimensionality reduction and solution manifold approximation

In this work, we propose a model order reduction framework to deal with inverse problems in a non-intrusive setting. Inverse problems, especially in a partial differential equation context, require a huge computational load due to the iterative optimization process. To accelerate such a procedure, we apply a numerical pipeline that involves artificial neural networks to parametrize the boundary conditions of the problem in hand, compress the dimensionality of the (full-order) snapshots, and approximate the parametric solution manifold. It derives a general framework capable to provide an ad-hoc parametrization of the inlet boundary and quickly converges to the optimal solution thanks to model order reduction. We present in this contribution the results obtained by applying such methods to two different CFD test cases.

A Continuous Convolutional Trainable Filter for Modelling Unstructured Data

Convolutional Neural Network (CNN) is one of the most important architectures in deep learning. The fundamental building block of a CNN is a trainable filter, represented as a discrete grid, used to perform convolution on discrete input data. In this work, we propose a continuous version of a trainable convolutional filter able to work also with unstructured data. This new framework allows exploring CNNs beyond discrete domains, enlarging the usage of this important learning technique for many more complex problems. Our experiments show that the continuous filter can achieve a level of accuracy comparable to the state-of-the-art discrete filter, and that it can be used in current deep learning architectures as a building block to solve problems with unstructured domains as well.

A Proper Orthogonal Decomposition approach for parameters reduction of Single Shot Detector networks

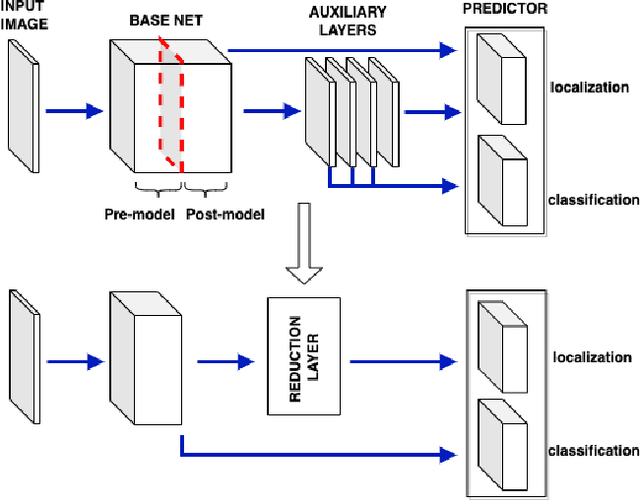
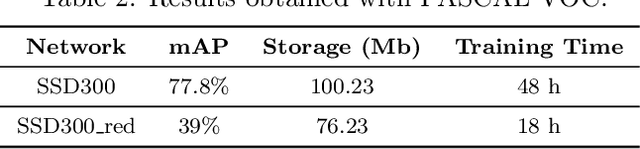
As a major breakthrough in artificial intelligence and deep learning, Convolutional Neural Networks have achieved an impressive success in solving many problems in several fields including computer vision and image processing. Real-time performance, robustness of algorithms and fast training processes remain open problems in these contexts. In addition object recognition and detection are challenging tasks for resource-constrained embedded systems, commonly used in the industrial sector. To overcome these issues, we propose a dimensionality reduction framework based on Proper Orthogonal Decomposition, a classical model order reduction technique, in order to gain a reduction in the number of hyperparameters of the net. We have applied such framework to SSD300 architecture using PASCAL VOC dataset, demonstrating a reduction of the network dimension and a remarkable speedup in the fine-tuning of the network in a transfer learning context.

An extended physics informed neural network for preliminary analysis of parametric optimal control problems

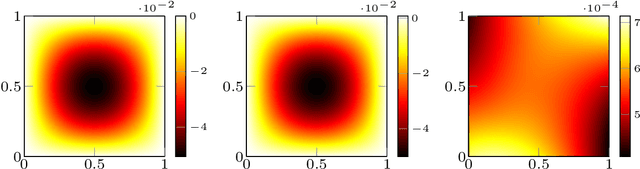
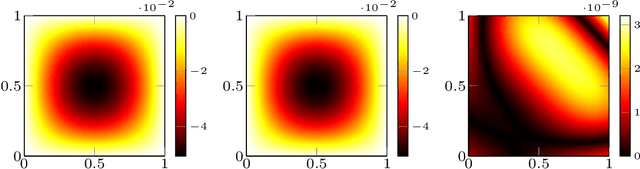
In this work we propose an extension of physics informed supervised learning strategies to parametric partial differential equations. Indeed, even if the latter are indisputably useful in many applications, they can be computationally expensive most of all in a real-time and many-query setting. Thus, our main goal is to provide a physics informed learning paradigm to simulate parametrized phenomena in a small amount of time. The physics information will be exploited in many ways, in the loss function (standard physics informed neural networks), as an augmented input (extra feature employment) and as a guideline to build an effective structure for the neural network (physics informed architecture). These three aspects, combined together, will lead to a faster training phase and to a more accurate parametric prediction. The methodology has been tested for several equations and also in an optimal control framework.

A Dimensionality Reduction Approach for Convolutional Neural Networks

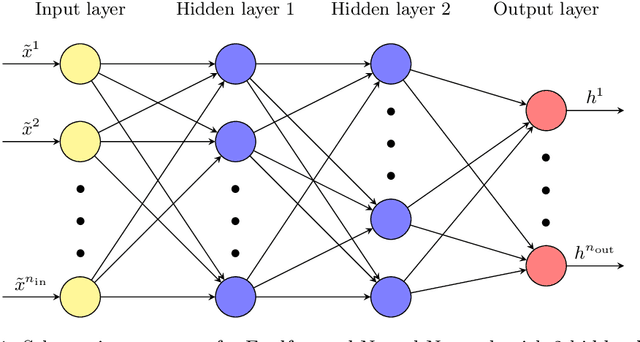
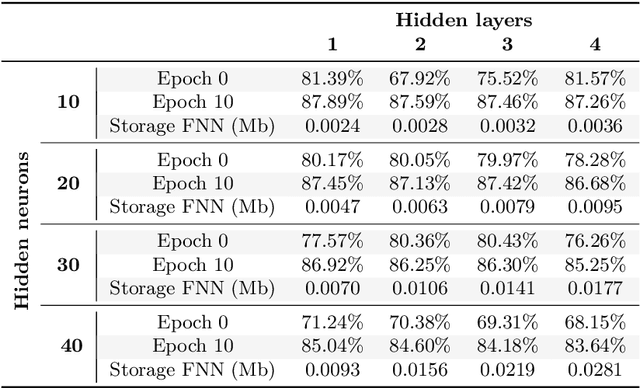
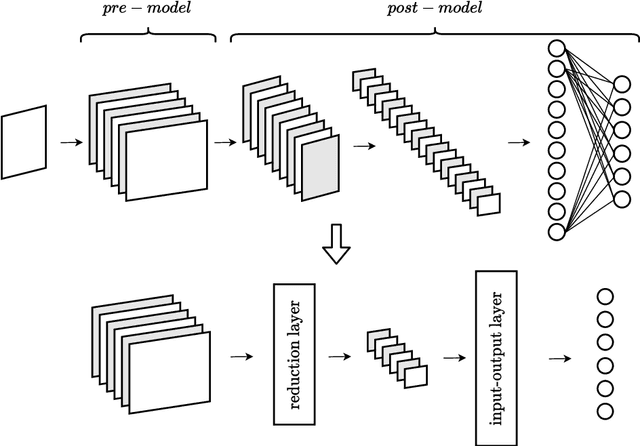
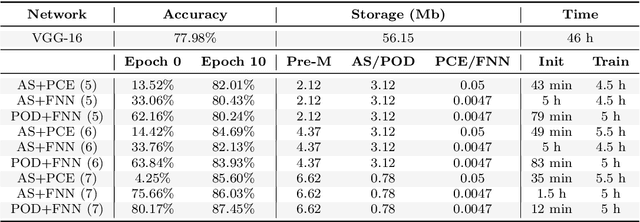
The focus of this paper is the application of classical model order reduction techniques, such as Active Subspaces and Proper Orthogonal Decomposition, to Deep Neural Networks. We propose a generic methodology to reduce the number of layers of a pre-trained network by combining the aforementioned techniques for dimensionality reduction with input-output mappings, such as Polynomial Chaos Expansion and Feedforward Neural Networks. The necessity of compressing the architecture of an existing Convolutional Neural Network is motivated by its application in embedded systems with specific storage constraints. Our experiment shows that the reduced nets obtained can achieve a level of accuracy similar to the original Convolutional Neural Network under examination, while saving in memory allocation.

The Neural Network shifted-Proper Orthogonal Decomposition: a Machine Learning Approach for Non-linear Reduction of Hyperbolic Equations

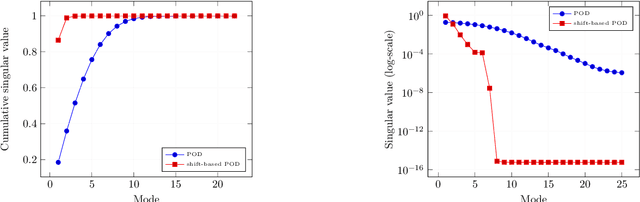
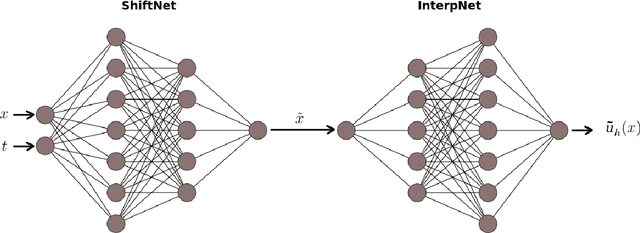
Models with dominant advection always posed a difficult challenge for projection-based reduced order modelling. Many methodologies that have recently been proposed are based on the pre-processing of the full-order solutions to accelerate the Kolmogorov N-width decay thereby obtaining smaller linear subspaces with improved accuracy. These methods however must rely on the knowledge of the characteristic speeds in phase space of the solution, limiting their range of applicability to problems with explicit functional form for the advection field. In this work we approach the problem of automatically detecting the correct pre-processing transformation in a statistical learning framework by implementing a deep-learning architecture. The purely data-driven method allowed us to generalise the existing approaches of linear subspace manipulation to non-linear hyperbolic problems with unknown advection fields. The proposed algorithm has been validated against simple test cases to benchmark its performances and later successfully applied to a multiphase simulation.