Optimal Transport-Based Displacement Interpolation with Data Augmentation for Reduced Order Modeling of Nonlinear Dynamical Systems

We present a novel reduced-order Model (ROM) that leverages optimal transport (OT) theory and displacement interpolation to enhance the representation of nonlinear dynamics in complex systems. While traditional ROM techniques face challenges in this scenario, especially when data (i.e., observational snapshots) is limited, our method addresses these issues by introducing a data augmentation strategy based on OT principles. The proposed framework generates interpolated solutions tracing geodesic paths in the space of probability distributions, enriching the training dataset for the ROM. A key feature of our approach is its ability to provide a continuous representation of the solution's dynamics by exploiting a virtual-to-real time mapping. This enables the reconstruction of solutions at finer temporal scales than those provided by the original data. To further improve prediction accuracy, we employ Gaussian Process Regression to learn the residual and correct the representation between the interpolated snapshots and the physical solution. We demonstrate the effectiveness of our methodology with atmospheric mesoscale benchmarks characterized by highly nonlinear, advection-dominated dynamics. Our results show improved accuracy and efficiency in predicting complex system behaviors, indicating the potential of this approach for a wide range of applications in computational physics and engineering.

The Neural Network shifted-Proper Orthogonal Decomposition: a Machine Learning Approach for Non-linear Reduction of Hyperbolic Equations

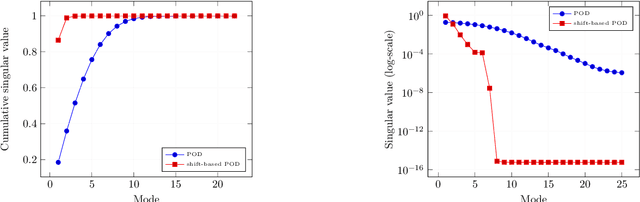
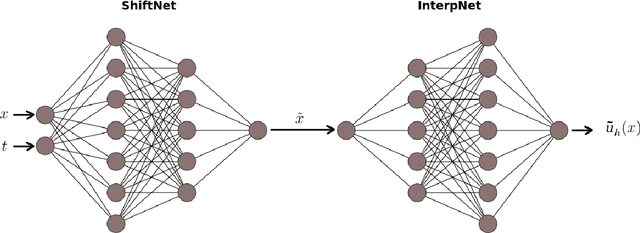
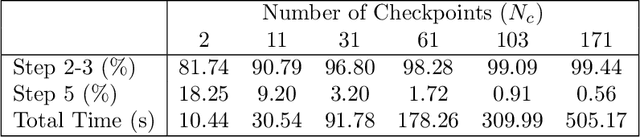
Models with dominant advection always posed a difficult challenge for projection-based reduced order modelling. Many methodologies that have recently been proposed are based on the pre-processing of the full-order solutions to accelerate the Kolmogorov N-width decay thereby obtaining smaller linear subspaces with improved accuracy. These methods however must rely on the knowledge of the characteristic speeds in phase space of the solution, limiting their range of applicability to problems with explicit functional form for the advection field. In this work we approach the problem of automatically detecting the correct pre-processing transformation in a statistical learning framework by implementing a deep-learning architecture. The purely data-driven method allowed us to generalise the existing approaches of linear subspace manipulation to non-linear hyperbolic problems with unknown advection fields. The proposed algorithm has been validated against simple test cases to benchmark its performances and later successfully applied to a multiphase simulation.