Non-linear manifold ROM with Convolutional Autoencoders and Reduced Over-Collocation method
Paper and Code
Mar 01, 2022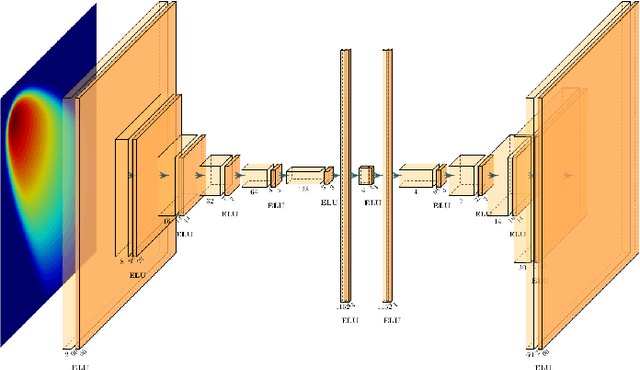

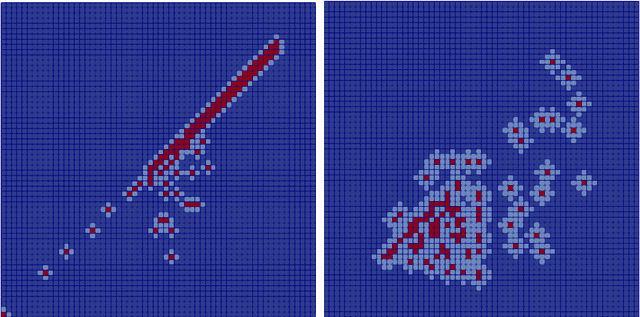

Non-affine parametric dependencies, nonlinearities and advection-dominated regimes of the model of interest can result in a slow Kolmogorov n-width decay, which precludes the realization of efficient reduced-order models based on linear subspace approximations. Among the possible solutions, there are purely data-driven methods that leverage autoencoders and their variants to learn a latent representation of the dynamical system, and then evolve it in time with another architecture. Despite their success in many applications where standard linear techniques fail, more has to be done to increase the interpretability of the results, especially outside the training range and not in regimes characterized by an abundance of data. Not to mention that none of the knowledge on the physics of the model is exploited during the predictive phase. In order to overcome these weaknesses, we implement the non-linear manifold method introduced by Carlberg et al [37] with hyper-reduction achieved through reduced over-collocation and teacher-student training of a reduced decoder. We test the methodology on a 2d non-linear conservation law and a 2d shallow water models, and compare the results obtained with a purely data-driven method for which the dynamics is evolved in time with a long-short term memory network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge