NeurIPS 2024 ML4CFD Competition: Results and Retrospective Analysis

The integration of machine learning (ML) into the physical sciences is reshaping computational paradigms, offering the potential to accelerate demanding simulations such as computational fluid dynamics (CFD). Yet, persistent challenges in accuracy, generalization, and physical consistency hinder the practical deployment of ML models in scientific domains. To address these limitations and systematically benchmark progress, we organized the ML4CFD competition, centered on surrogate modeling for aerodynamic simulations over two-dimensional airfoils. The competition attracted over 240 teams, who were provided with a curated dataset generated via OpenFOAM and evaluated through a multi-criteria framework encompassing predictive accuracy, physical fidelity, computational efficiency, and out-of-distribution generalization. This retrospective analysis reviews the competition outcomes, highlighting several approaches that outperformed baselines under our global evaluation score. Notably, the top entry exceeded the performance of the original OpenFOAM solver on aggregate metrics, illustrating the promise of ML-based surrogates to outperform traditional solvers under tailored criteria. Drawing from these results, we analyze the key design principles of top submissions, assess the robustness of our evaluation framework, and offer guidance for future scientific ML challenges.

Geometry aware inference of steady state PDEs using Equivariant Neural Fields representations

Recent advances in Neural Fields have enabled powerful, discretization-invariant methods for learning neural operators that approximate solutions of Partial Differential Equations (PDEs) on general geometries. Building on these developments, we introduce enf2enf, an encoder--decoder methodology for predicting steady-state Partial Differential Equations with non-parameterized geometric variability, based on recently proposed Equivariant Neural Field architectures. In enf2enf, input geometries are encoded into latent point cloud embeddings that inherently preserve geometric grounding and capture local phenomena. The resulting representations are then combined with global parameters and directly decoded into continuous output fields, thus efficiently modeling the coupling between geometry and physics. By leveraging the inductive biases of locality and translation invariance, our approach is able to capture fine-scale physical features as well as complex shape variations, thereby enhancing generalization and physical compliance. Extensive experiments on a high-fidelity aerodynamic dataset, a hyper-elastic material benchmark, and multi-element airfoil geometries, demonstrate that the proposed model achieves superior or competitive performance compared to state-of-the-art graph based, operator learning, and neural field methods. Notably, our method supports real time inference and zero-shot super-resolution, enabling efficient training on low-resolution meshes while maintaining high accuracy on full-scale discretizations.

Bayesian optimization for mixed variables using an adaptive dimension reduction process: applications to aircraft design

Multidisciplinary design optimization methods aim at adapting numerical optimization techniques to the design of engineering systems involving multiple disciplines. In this context, a large number of mixed continuous, integer and categorical variables might arise during the optimization process and practical applications involve a large number of design variables. Recently, there has been a growing interest in mixed variables constrained Bayesian optimization but most existing approaches severely increase the number of the hyperparameters related to the surrogate model. In this paper, we address this issue by constructing surrogate models using less hyperparameters. The reduction process is based on the partial least squares method. An adaptive procedure for choosing the number of hyperparameters is proposed. The performance of the proposed approach is confirmed on analytical tests as well as two real applications related to aircraft design. A significant improvement is obtained compared to genetic algorithms.

Regularized infill criteria for multi-objective Bayesian optimization with application to aircraft design

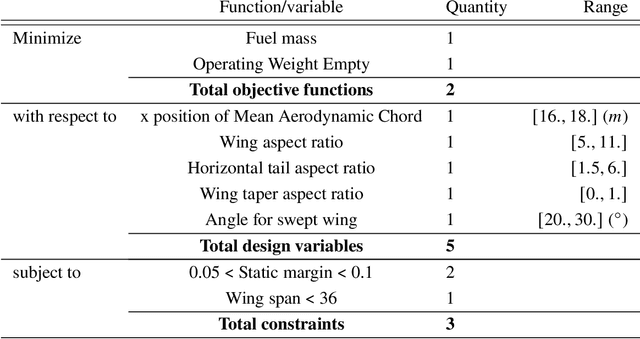
Bayesian optimization is an advanced tool to perform ecient global optimization It consists on enriching iteratively surrogate Kriging models of the objective and the constraints both supposed to be computationally expensive of the targeted optimization problem Nowadays efficient extensions of Bayesian optimization to solve expensive multiobjective problems are of high interest The proposed method in this paper extends the super efficient global optimization with mixture of experts SEGOMOE to solve constrained multiobjective problems To cope with the illposedness of the multiobjective inll criteria different enrichment procedures using regularization techniques are proposed The merit of the proposed approaches are shown on known multiobjective benchmark problems with and without constraints The proposed methods are then used to solve a biobjective application related to conceptual aircraft design with ve unknown design variables and three nonlinear inequality constraints The preliminary results show a reduction of the total cost in terms of function evaluations by a factor of 20 compared to the evolutionary algorithm NSGA-II.

Bayesian Optimization of a Lightweight and Accurate Neural Network for Aerodynamic Performance Prediction

Ensuring high accuracy and efficiency of predictive models is paramount in the aerospace industry, particularly in the context of multidisciplinary design and optimization processes. These processes often require numerous evaluations of complex objective functions, which can be computationally expensive and time-consuming. To build efficient and accurate predictive models, we propose a new approach that leverages Bayesian Optimization (BO) to optimize the hyper-parameters of a lightweight and accurate Neural Network (NN) for aerodynamic performance prediction. To clearly describe the interplay between design variables, hierarchical and categorical kernels are used in the BO formulation. We demonstrate the efficiency of our approach through two comprehensive case studies, where the optimized NN significantly outperforms baseline models and other publicly available NNs in terms of accuracy and parameter efficiency. For the drag coefficient prediction task, the Mean Absolute Percentage Error (MAPE) of our optimized model drops from 0.1433\% to 0.0163\%, which is nearly an order of magnitude improvement over the baseline model. Additionally, our model achieves a MAPE of 0.82\% on a benchmark aircraft self-noise prediction problem, significantly outperforming existing models (where their MAPE values are around 2 to 3\%) while requiring less computational resources. The results highlight the potential of our framework to enhance the scalability and performance of NNs in large-scale MDO problems, offering a promising solution for the aerospace industry.

Aero-Nef: Neural Fields for Rapid Aircraft Aerodynamics Simulations

This paper presents a methodology to learn surrogate models of steady state fluid dynamics simulations on meshed domains, based on Implicit Neural Representations (INRs). The proposed models can be applied directly to unstructured domains for different flow conditions, handle non-parametric 3D geometric variations, and generalize to unseen shapes at test time. The coordinate-based formulation naturally leads to robustness with respect to discretization, allowing an excellent trade-off between computational cost (memory footprint and training time) and accuracy. The method is demonstrated on two industrially relevant applications: a RANS dataset of the two-dimensional compressible flow over a transonic airfoil and a dataset of the surface pressure distribution over 3D wings, including shape, inflow condition, and control surface deflection variations. On the considered test cases, our approach achieves a more than three times lower test error and significantly improves generalization error on unseen geometries compared to state-of-the-art Graph Neural Network architectures. Remarkably, the method can perform inference five order of magnitude faster than the high fidelity solver on the RANS transonic airfoil dataset. Code is available at https://gitlab.isae-supaero.fr/gi.catalani/aero-nepf

High-dimensional mixed-categorical Gaussian processes with application to multidisciplinary design optimization for a green aircraft

Multidisciplinary design optimization (MDO) methods aim at adapting numerical optimization techniques to the design of engineering systems involving multiple disciplines. In this context, a large number of mixed continuous, integer, and categorical variables might arise during the optimization process, and practical applications involve a significant number of design variables. Recently, there has been a growing interest in mixed-categorical metamodels based on Gaussian Process (GP) for Bayesian optimization. In particular, to handle mixed-categorical variables, several existing approaches employ different strategies to build the GP. These strategies either use continuous kernels, such as the continuous relaxation or the Gower distance-based kernels, or direct estimation of the correlation matrix, such as the exponential homoscedastic hypersphere (EHH) or the Homoscedastic Hypersphere (HH) kernel. Although the EHH and HH kernels are shown to be very efficient and lead to accurate GPs, they are based on a large number of hyperparameters. In this paper, we address this issue by constructing mixed-categorical GPs with fewer hyperparameters using Partial Least Squares (PLS) regression. Our goal is to generalize Kriging with PLS, commonly used for continuous inputs, to handle mixed-categorical inputs. The proposed method is implemented in the open-source software SMT and has been efficiently applied to structural and multidisciplinary applications. Our method is used to effectively demonstrate the structural behavior of a cantilever beam and facilitates MDO of a green aircraft, resulting in a 439-kilogram reduction in the amount of fuel consumed during a single aircraft mission.

SMT 2.0: A Surrogate Modeling Toolbox with a focus on Hierarchical and Mixed Variables Gaussian Processes

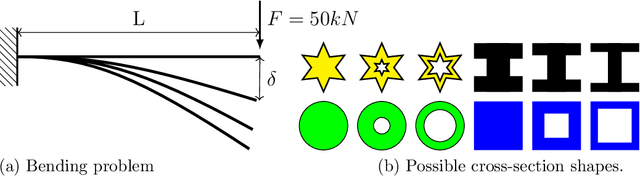
The Surrogate Modeling Toolbox (SMT) is an open-source Python package that offers a collection of surrogate modeling methods, sampling techniques, and a set of sample problems. This paper presents SMT 2.0, a major new release of SMT that introduces significant upgrades and new features to the toolbox. This release adds the capability to handle mixed-variable surrogate models and hierarchical variables. These types of variables are becoming increasingly important in several surrogate modeling applications. SMT 2.0 also improves SMT by extending sampling methods, adding new surrogate models, and computing variance and kernel derivatives for Kriging. This release also includes new functions to handle noisy and use multifidelity data. To the best of our knowledge, SMT 2.0 is the first open-source surrogate library to propose surrogate models for hierarchical and mixed inputs. This open-source software is distributed under the New BSD license.