Nathalie Bartoli
ONERA, DTIS, Universitée de Toulouse, Toulouse, France
Surrogate-based optimization of system architectures subject to hidden constraints
Apr 11, 2025Abstract:The exploration of novel architectures requires physics-based simulation due to a lack of prior experience to start from, which introduces two specific challenges for optimization algorithms: evaluations become more expensive (in time) and evaluations might fail. The former challenge is addressed by Surrogate-Based Optimization (SBO) algorithms, in particular Bayesian Optimization (BO) using Gaussian Process (GP) models. An overview is provided of how BO can deal with challenges specific to architecture optimization, such as design variable hierarchy and multiple objectives: specific measures include ensemble infills and a hierarchical sampling algorithm. Evaluations might fail due to non-convergence of underlying solvers or infeasible geometry in certain areas of the design space. Such failed evaluations, also known as hidden constraints, pose a particular challenge to SBO/BO, as the surrogate model cannot be trained on empty results. This work investigates various strategies for satisfying hidden constraints in BO algorithms. Three high-level strategies are identified: rejection of failed points from the training set, replacing failed points based on viable (non-failed) points, and predicting the failure region. Through investigations on a set of test problems including a jet engine architecture optimization problem, it is shown that best performance is achieved with a mixed-discrete GP to predict the Probability of Viability (PoV), and by ensuring selected infill points satisfy some minimum PoV threshold. This strategy is demonstrated by solving a jet engine architecture problem that features at 50% failure rate and could not previously be solved by a BO algorithm. The developed BO algorithm and used test problems are available in the open-source Python library SBArchOpt.
Regularized infill criteria for multi-objective Bayesian optimization with application to aircraft design
Apr 11, 2025


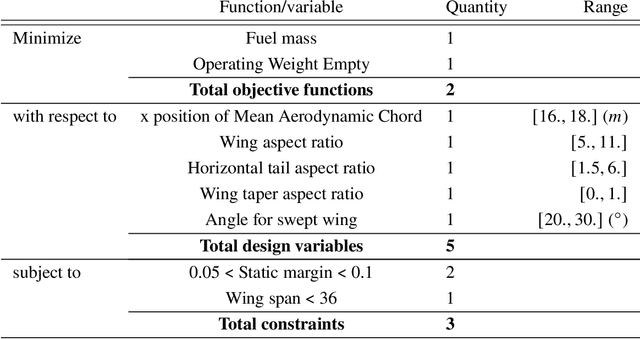
Abstract:Bayesian optimization is an advanced tool to perform ecient global optimization It consists on enriching iteratively surrogate Kriging models of the objective and the constraints both supposed to be computationally expensive of the targeted optimization problem Nowadays efficient extensions of Bayesian optimization to solve expensive multiobjective problems are of high interest The proposed method in this paper extends the super efficient global optimization with mixture of experts SEGOMOE to solve constrained multiobjective problems To cope with the illposedness of the multiobjective inll criteria different enrichment procedures using regularization techniques are proposed The merit of the proposed approaches are shown on known multiobjective benchmark problems with and without constraints The proposed methods are then used to solve a biobjective application related to conceptual aircraft design with ve unknown design variables and three nonlinear inequality constraints The preliminary results show a reduction of the total cost in terms of function evaluations by a factor of 20 compared to the evolutionary algorithm NSGA-II.
Bayesian optimization for mixed variables using an adaptive dimension reduction process: applications to aircraft design
Apr 11, 2025Abstract:Multidisciplinary design optimization methods aim at adapting numerical optimization techniques to the design of engineering systems involving multiple disciplines. In this context, a large number of mixed continuous, integer and categorical variables might arise during the optimization process and practical applications involve a large number of design variables. Recently, there has been a growing interest in mixed variables constrained Bayesian optimization but most existing approaches severely increase the number of the hyperparameters related to the surrogate model. In this paper, we address this issue by constructing surrogate models using less hyperparameters. The reduction process is based on the partial least squares method. An adaptive procedure for choosing the number of hyperparameters is proposed. The performance of the proposed approach is confirmed on analytical tests as well as two real applications related to aircraft design. A significant improvement is obtained compared to genetic algorithms.
High-dimensional mixed-categorical Gaussian processes with application to multidisciplinary design optimization for a green aircraft
Nov 10, 2023Abstract:Multidisciplinary design optimization (MDO) methods aim at adapting numerical optimization techniques to the design of engineering systems involving multiple disciplines. In this context, a large number of mixed continuous, integer, and categorical variables might arise during the optimization process, and practical applications involve a significant number of design variables. Recently, there has been a growing interest in mixed-categorical metamodels based on Gaussian Process (GP) for Bayesian optimization. In particular, to handle mixed-categorical variables, several existing approaches employ different strategies to build the GP. These strategies either use continuous kernels, such as the continuous relaxation or the Gower distance-based kernels, or direct estimation of the correlation matrix, such as the exponential homoscedastic hypersphere (EHH) or the Homoscedastic Hypersphere (HH) kernel. Although the EHH and HH kernels are shown to be very efficient and lead to accurate GPs, they are based on a large number of hyperparameters. In this paper, we address this issue by constructing mixed-categorical GPs with fewer hyperparameters using Partial Least Squares (PLS) regression. Our goal is to generalize Kriging with PLS, commonly used for continuous inputs, to handle mixed-categorical inputs. The proposed method is implemented in the open-source software SMT and has been efficiently applied to structural and multidisciplinary applications. Our method is used to effectively demonstrate the structural behavior of a cantilever beam and facilitates MDO of a green aircraft, resulting in a 439-kilogram reduction in the amount of fuel consumed during a single aircraft mission.
SMT 2.0: A Surrogate Modeling Toolbox with a focus on Hierarchical and Mixed Variables Gaussian Processes
May 23, 2023


Abstract:The Surrogate Modeling Toolbox (SMT) is an open-source Python package that offers a collection of surrogate modeling methods, sampling techniques, and a set of sample problems. This paper presents SMT 2.0, a major new release of SMT that introduces significant upgrades and new features to the toolbox. This release adds the capability to handle mixed-variable surrogate models and hierarchical variables. These types of variables are becoming increasingly important in several surrogate modeling applications. SMT 2.0 also improves SMT by extending sampling methods, adding new surrogate models, and computing variance and kernel derivatives for Kriging. This release also includes new functions to handle noisy and use multifidelity data. To the best of our knowledge, SMT 2.0 is the first open-source surrogate library to propose surrogate models for hierarchical and mixed inputs. This open-source software is distributed under the New BSD license.
Variance based sensitivity analysis for Monte Carlo and importance sampling reliability assessment with Gaussian processes
Nov 30, 2020



Abstract:Running a reliability analysis on engineering problems involving complex numerical models can be computationally very expensive, requiring advanced simulation methods to reduce the overall numerical cost. Gaussian process based active learning methods for reliability analysis have emerged as a promising way for reducing this computational cost. The learning phase of these methods consists in building a Gaussian process surrogate model of the performance function and using the uncertainty structure of the Gaussian process to enrich iteratively this surrogate model. For that purpose a learning criterion has to be defined. Then, the estimation of the probability of failure is typically obtained by a classification of a population evaluated on the final surrogate model. Hence, the estimator of the probability of failure holds two different uncertainty sources related to the surrogate model approximation and to the sampling based integration technique. In this paper, we propose a methodology to quantify the sensitivity of the probability of failure estimator to both uncertainty sources. This analysis also enables to control the whole error associated to the failure probability estimate and thus provides an accuracy criterion on the estimation. Thus, an active learning approach integrating this analysis to reduce the main source of error and stopping when the global variability is sufficiently low is introduced. The approach is proposed for both a Monte Carlo based method as well as an importance sampling based method, seeking to improve the estimation of rare event probabilities. Performance of the proposed strategy is then assessed on several examples.
An efficient application of Bayesian optimization to an industrial MDO framework for aircraft design
Jun 12, 2020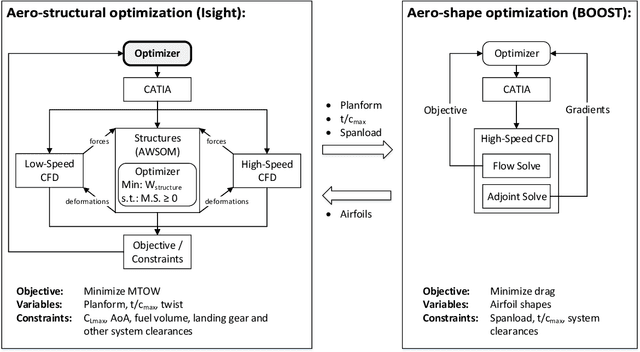


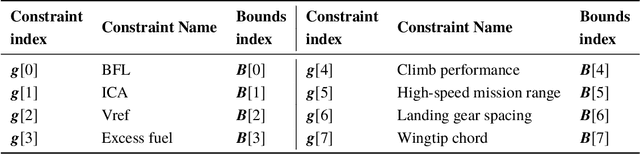
Abstract:The multi-level, multi-disciplinary and multi-fidelity optimization framework developed at Bombardier Aviation has shown great results to explore efficient and competitive aircraft configurations. This optimization framework has been developed within the Isight software, the latter offers a set of ready-to-use optimizers. Unfortunately, the computational effort required by the Isight optimizers can be prohibitive with respect to the requirements of an industrial context. In this paper, a constrained Bayesian optimization optimizer, namely the super efficient global optimization with mixture of experts, is used to reduce the optimization computational effort. The obtained results showed significant improvements compared to two of the popular Isight optimizers. The capabilities of the tested constrained Bayesian optimization solver are demonstrated on Bombardier research aircraft configuration study cases.
Upper Trust Bound Feasibility Criterion for Mixed Constrained Bayesian Optimization with Application to Aircraft Design
May 12, 2020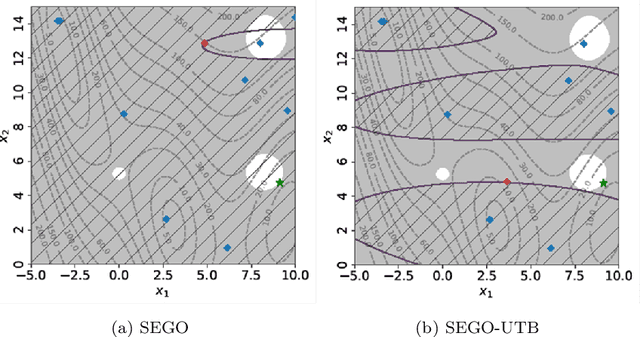
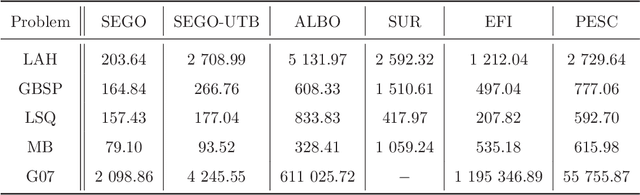
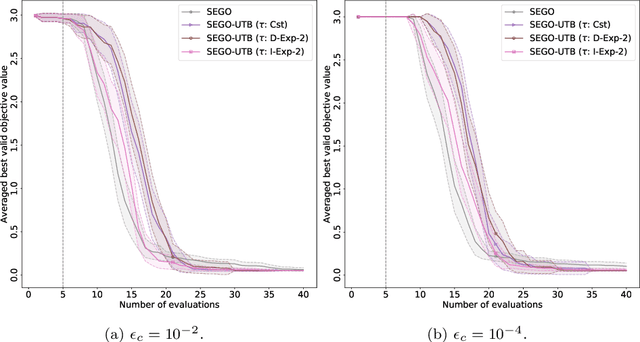
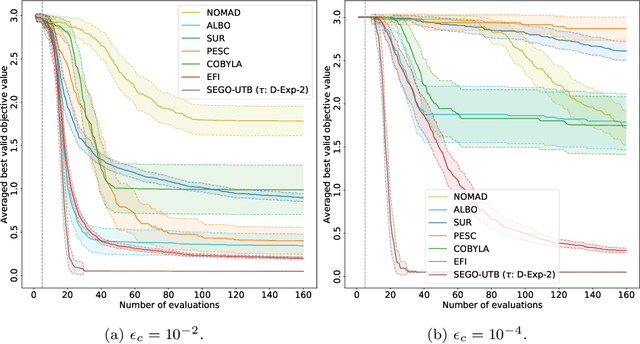
Abstract:Bayesian optimization methods have been successfully applied to black box optimization problems that are expensive to evaluate. In this paper, we adapt the so-called super effcient global optimization algorithm to solve more accurately mixed constrained problems. The proposed approach handles constraints by means of upper trust bound, the latter encourages exploration of the feasible domain by combining the mean prediction and the associated uncertainty function given by the Gaussian processes. On top of that, a refinement procedure, based on a learning rate criterion, is introduced to enhance the exploitation and exploration trade-off. We show the good potential of the approach on a set of numerical experiments. Finally, we present an application to conceptual aircraft configuration upon which we show the superiority of the proposed approach compared to a set of the state-of-the-art black box optimization solvers. Keywords: Global Optimization, Mixed Constrained Optimization, Black box optimization, Bayesian Optimization, Gaussian Process.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge