Aero-Nef: Neural Fields for Rapid Aircraft Aerodynamics Simulations

This paper presents a methodology to learn surrogate models of steady state fluid dynamics simulations on meshed domains, based on Implicit Neural Representations (INRs). The proposed models can be applied directly to unstructured domains for different flow conditions, handle non-parametric 3D geometric variations, and generalize to unseen shapes at test time. The coordinate-based formulation naturally leads to robustness with respect to discretization, allowing an excellent trade-off between computational cost (memory footprint and training time) and accuracy. The method is demonstrated on two industrially relevant applications: a RANS dataset of the two-dimensional compressible flow over a transonic airfoil and a dataset of the surface pressure distribution over 3D wings, including shape, inflow condition, and control surface deflection variations. On the considered test cases, our approach achieves a more than three times lower test error and significantly improves generalization error on unseen geometries compared to state-of-the-art Graph Neural Network architectures. Remarkably, the method can perform inference five order of magnitude faster than the high fidelity solver on the RANS transonic airfoil dataset. Code is available at https://gitlab.isae-supaero.fr/gi.catalani/aero-nepf

Using neural networks to solve the 2D Poisson equation for electric field computation in plasma fluid simulations

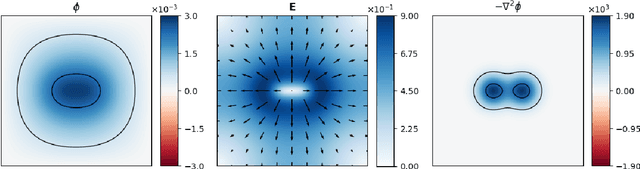
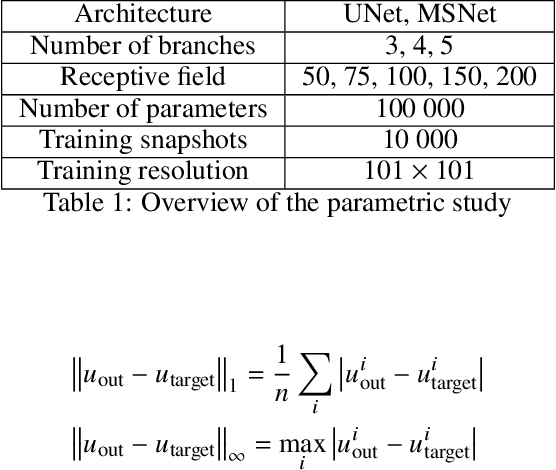
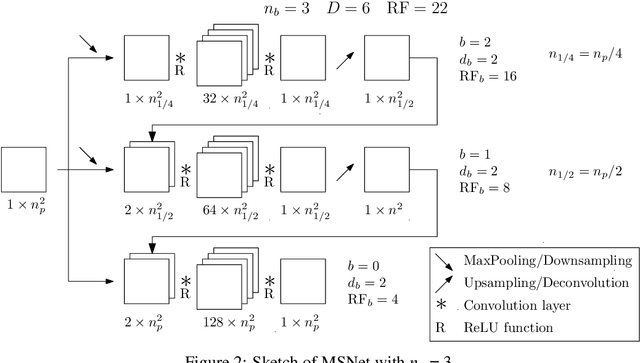
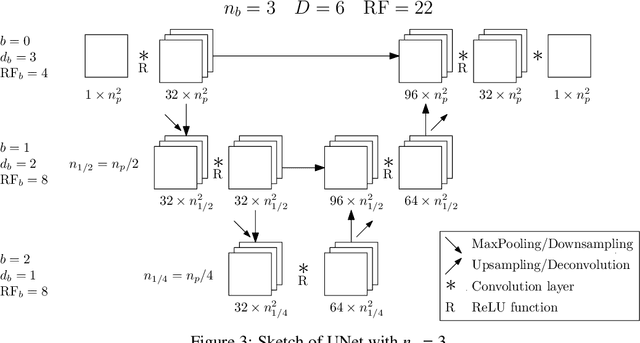
The Poisson equation is critical to get a self-consistent solution in plasma fluid simulations used for Hall effect thrusters and streamers discharges. Solving the 2D Poisson equation with zero Dirichlet boundary conditions using a deep neural network is investigated using multiple-scale architectures, defined in terms of number of branches, depth and receptive field. The latter is found critical to correctly capture large topological structures of the field. The investigation of multiple architectures, losses, and hyperparameters provides an optimum network to solve accurately the steady Poisson problem. Generalization to new resolutions and domain sizes is then proposed using a proper scaling of the network. Finally, found neural network solver, called PlasmaNet, is coupled with an unsteady Euler plasma fluid equations solver. The test case corresponds to electron plasma oscillations which is used to assess the accuracy of the neural network solution in a time-dependent simulation. In this time-evolving problem, a physical loss is necessary to produce a stable simulation. PlasmaNet is then benchmarked on meshes with increasing number of nodes, and compared with an existing solver based on a standard linear system algorithm for the Poisson equation. It outperforms the classical plasma solver, up to speedups 700 times faster on large meshes. PlasmaNet is finally tested on a more complex case of discharge propagation involving chemistry and advection. The guidelines established in previous sections are applied to build the CNN to solve the same Poisson equation but in cylindrical coordinates. Results reveal good CNN predictions with significant speedup. These results pave the way to new computational strategies to predict unsteady problems involving a Poisson equation, including configurations with coupled multiphysics interactions such as in plasma flows.

Effects of boundary conditions in fully convolutional networks for learning spatio-temporal dynamics

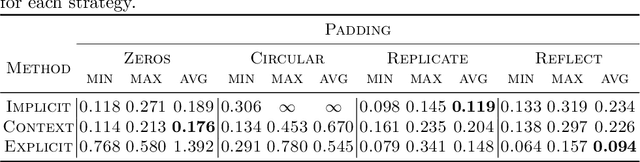
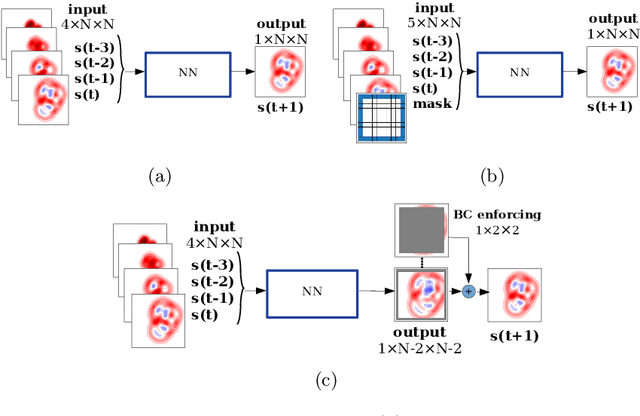
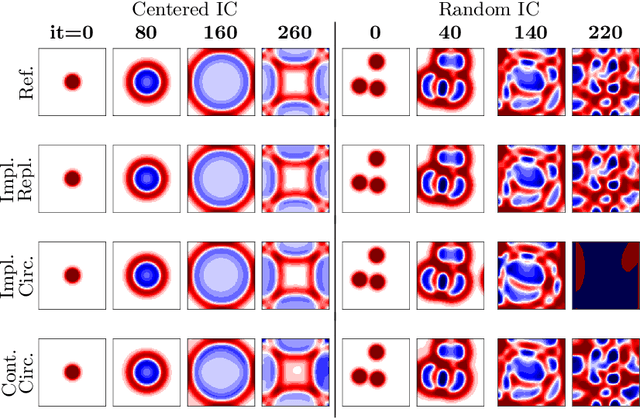
Accurate modeling of boundary conditions is crucial in computational physics. The ever increasing use of neural networks as surrogates for physics-related problems calls for an improved understanding of boundary condition treatment, and its influence on the network accuracy. In this paper, several strategies to impose boundary conditions (namely padding, improved spatial context, and explicit encoding of physical boundaries) are investigated in the context of fully convolutional networks applied to recurrent tasks. These strategies are evaluated on two spatio-temporal evolving problems modeled by partial differential equations: the 2D propagation of acoustic waves (hyperbolic PDE) and the heat equation (parabolic PDE). Results reveal a high sensitivity of both accuracy and stability on the boundary implementation in such recurrent tasks. It is then demonstrated that the choice of the optimal padding strategy is directly linked to the data semantics. Furthermore, the inclusion of additional input spatial context or explicit physics-based rules allows a better handling of boundaries in particular for large number of recurrences, resulting in more robust and stable neural networks, while facilitating the design and versatility of such networks.