Using neural networks to solve the 2D Poisson equation for electric field computation in plasma fluid simulations

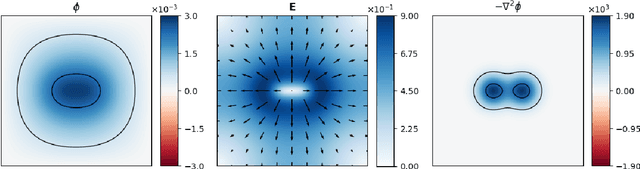
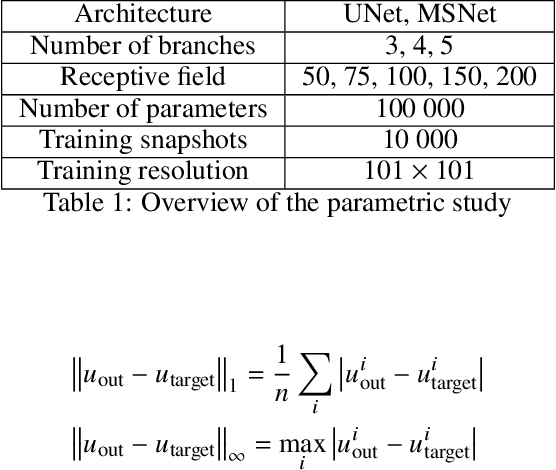
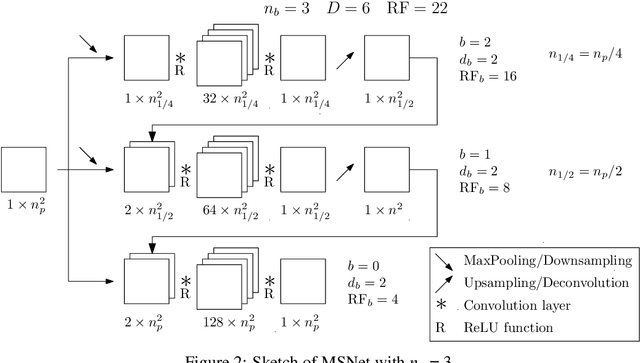
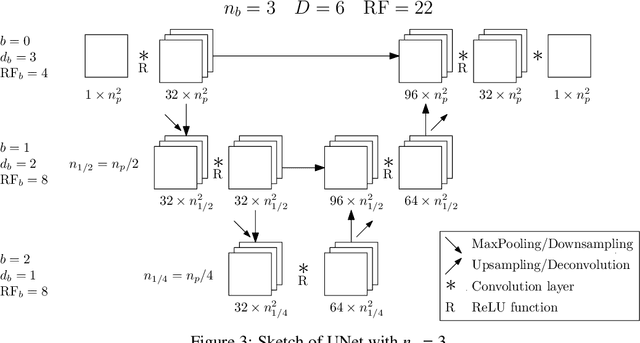
The Poisson equation is critical to get a self-consistent solution in plasma fluid simulations used for Hall effect thrusters and streamers discharges. Solving the 2D Poisson equation with zero Dirichlet boundary conditions using a deep neural network is investigated using multiple-scale architectures, defined in terms of number of branches, depth and receptive field. The latter is found critical to correctly capture large topological structures of the field. The investigation of multiple architectures, losses, and hyperparameters provides an optimum network to solve accurately the steady Poisson problem. Generalization to new resolutions and domain sizes is then proposed using a proper scaling of the network. Finally, found neural network solver, called PlasmaNet, is coupled with an unsteady Euler plasma fluid equations solver. The test case corresponds to electron plasma oscillations which is used to assess the accuracy of the neural network solution in a time-dependent simulation. In this time-evolving problem, a physical loss is necessary to produce a stable simulation. PlasmaNet is then benchmarked on meshes with increasing number of nodes, and compared with an existing solver based on a standard linear system algorithm for the Poisson equation. It outperforms the classical plasma solver, up to speedups 700 times faster on large meshes. PlasmaNet is finally tested on a more complex case of discharge propagation involving chemistry and advection. The guidelines established in previous sections are applied to build the CNN to solve the same Poisson equation but in cylindrical coordinates. Results reveal good CNN predictions with significant speedup. These results pave the way to new computational strategies to predict unsteady problems involving a Poisson equation, including configurations with coupled multiphysics interactions such as in plasma flows.

Performance and accuracy assessments of an incompressible fluid solver coupled with a deep Convolutional Neural Network

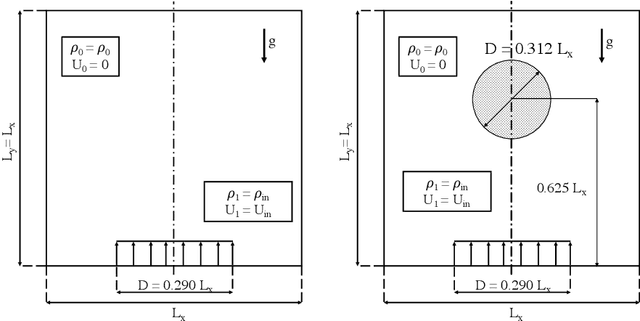
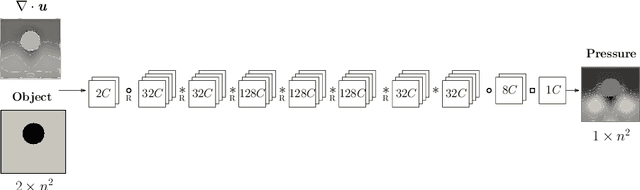
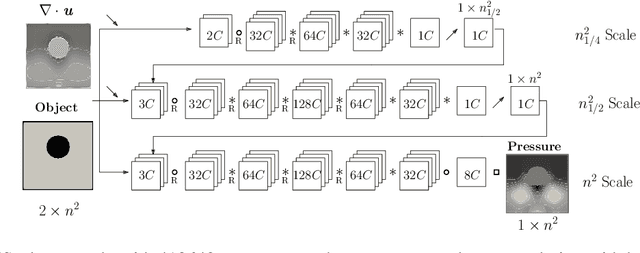
The resolution of the Poisson equation is usually one of the most computationally intensive steps for incompressible fluid solvers. Lately, Deep Learning, and especially Convolutional Neural Networks (CNN), has been introduced to solve this equation, leading to significant inference time reduction at the cost of a lack of guarantee on the accuracy of the solution. This drawback might lead to inaccuracies and potentially unstable simulations. It also makes impossible a fair assessment of the CNN speedup, for instance, when changing the network architecture, since evaluated at different error levels. To circumvent this issue, a hybrid strategy is developed, which couples a CNN with a traditional iterative solver to ensure a user-defined accuracy level. The CNN hybrid method is tested on two flow cases, consisting of a variable-density plume with and without obstacles, demostrating remarkable generalization capabilities, ensuring both the accuracy and stability of the simulations. The error distribution of the predictions using several network architectures is further investigated. Results show that the threshold of the hybrid strategy defined as the mean divergence of the velocity field is ensuring a consistent physical behavior of the CNN-based hybrid computational strategy. This strategy allows a systematic evaluation of the CNN performance at the same accuracy level for various network architectures. In particular, the importance of incorporating multiple scales in the network architecture is demonstrated, since improving both the accuracy and the inference performance compared with feedforward CNN architectures, as these networks can provide solutions 1 10-25 faster than traditional iterative solvers.