Automatic Parameterization for Aerodynamic Shape Optimization via Deep Geometric Learning

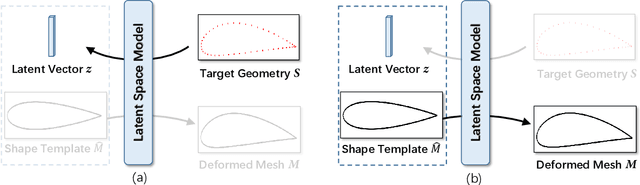
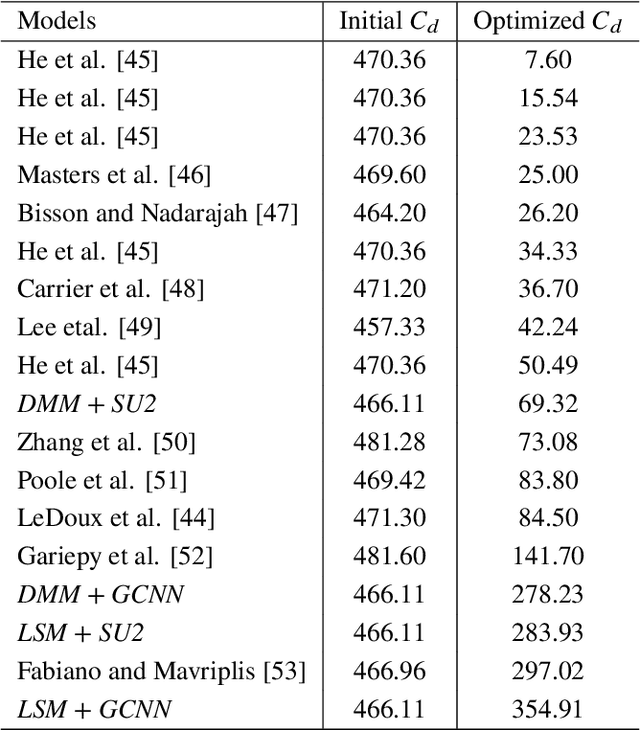
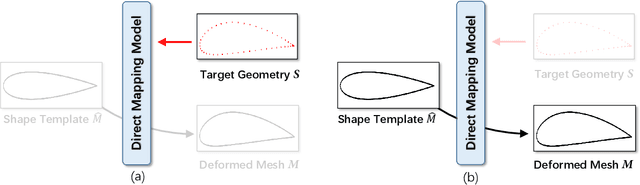
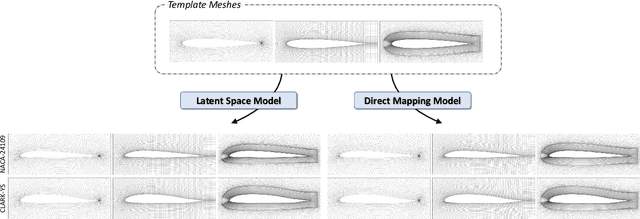
We propose two deep learning models that fully automate shape parameterization for aerodynamic shape optimization. Both models are optimized to parameterize via deep geometric learning to embed human prior knowledge into learned geometric patterns, eliminating the need for further handcrafting. The Latent Space Model (LSM) learns a low-dimensional latent representation of an object from a dataset of various geometries, while the Direct Mapping Model (DMM) builds parameterization on the fly using only one geometry of interest. We also devise a novel regularization loss that efficiently integrates volumetric mesh deformation into the parameterization model. The models directly manipulate the high-dimensional mesh data by moving vertices. LSM and DMM are fully differentiable, enabling gradient-based, end-to-end pipeline design and plug-and-play deployment of surrogate models or adjoint solvers. We perform shape optimization experiments on 2D airfoils and discuss the applicable scenarios for the two models.

Performance and accuracy assessments of an incompressible fluid solver coupled with a deep Convolutional Neural Network

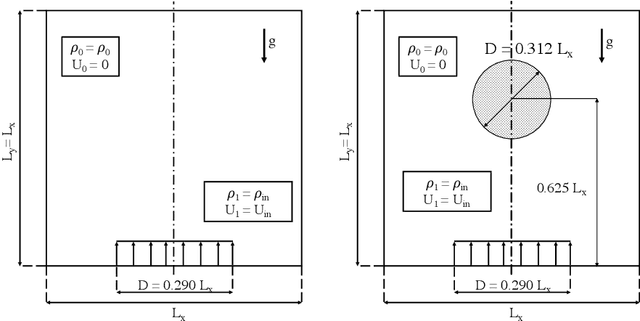
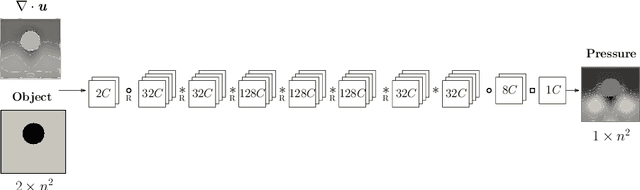
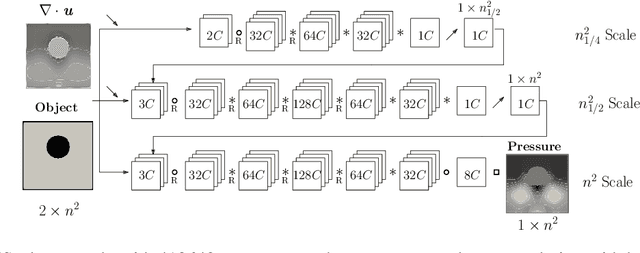
The resolution of the Poisson equation is usually one of the most computationally intensive steps for incompressible fluid solvers. Lately, Deep Learning, and especially Convolutional Neural Networks (CNN), has been introduced to solve this equation, leading to significant inference time reduction at the cost of a lack of guarantee on the accuracy of the solution. This drawback might lead to inaccuracies and potentially unstable simulations. It also makes impossible a fair assessment of the CNN speedup, for instance, when changing the network architecture, since evaluated at different error levels. To circumvent this issue, a hybrid strategy is developed, which couples a CNN with a traditional iterative solver to ensure a user-defined accuracy level. The CNN hybrid method is tested on two flow cases, consisting of a variable-density plume with and without obstacles, demostrating remarkable generalization capabilities, ensuring both the accuracy and stability of the simulations. The error distribution of the predictions using several network architectures is further investigated. Results show that the threshold of the hybrid strategy defined as the mean divergence of the velocity field is ensuring a consistent physical behavior of the CNN-based hybrid computational strategy. This strategy allows a systematic evaluation of the CNN performance at the same accuracy level for various network architectures. In particular, the importance of incorporating multiple scales in the network architecture is demonstrated, since improving both the accuracy and the inference performance compared with feedforward CNN architectures, as these networks can provide solutions 1 10-25 faster than traditional iterative solvers.

On the reproducibility of fully convolutional neural networks for modeling time-space evolving physical systems

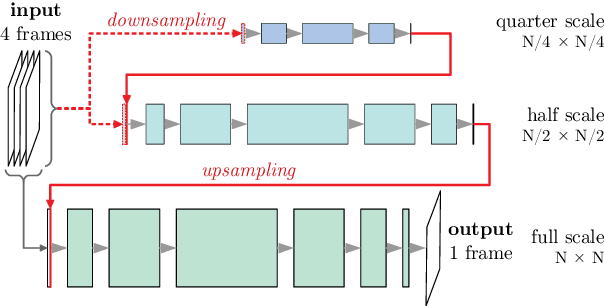
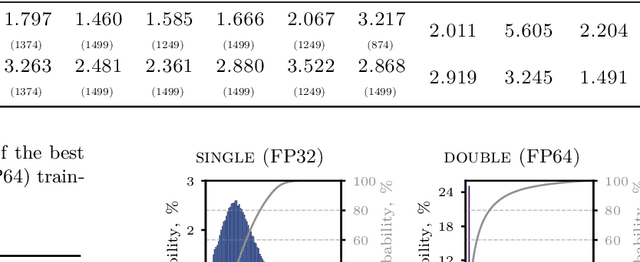
Reproducibility of a deep-learning fully convolutional neural network is evaluated by training several times the same network on identical conditions (database, hyperparameters, hardware) with non-deterministic Graphics Processings Unit (GPU) operations. The propagation of two-dimensional acoustic waves, typical of time-space evolving physical systems, is studied on both recursive and non-recursive tasks. Significant changes in models properties (weights, featured fields) are observed. When tested on various propagation benchmarks, these models systematically returned estimations with a high level of deviation, especially for the recurrent analysis which strongly amplifies variability due to the non-determinism. Trainings performed with double floating-point precision provide slightly better estimations and a significant reduction of the variability of both the network parameters and its testing error range.