Effects of boundary conditions in fully convolutional networks for learning spatio-temporal dynamics

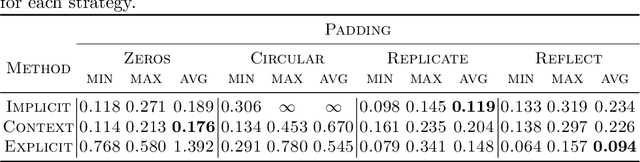
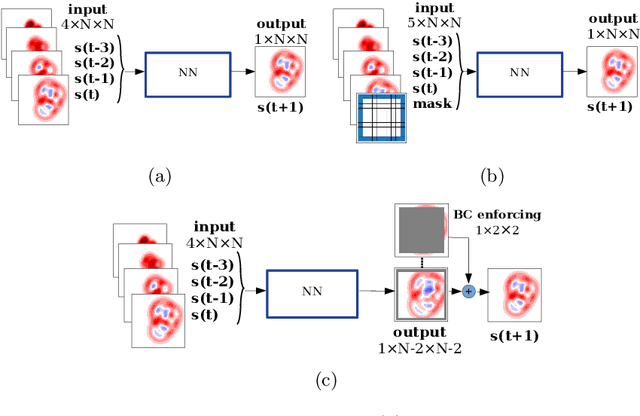
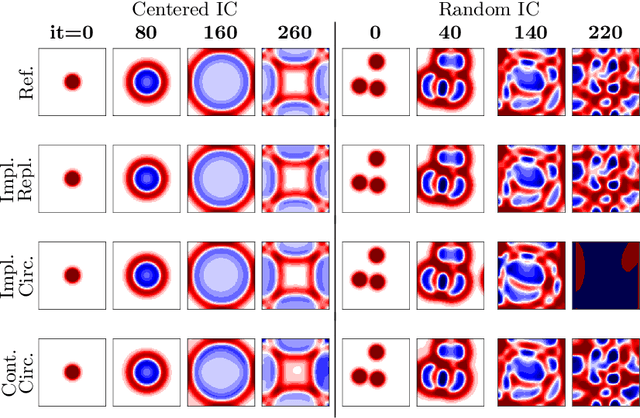
Accurate modeling of boundary conditions is crucial in computational physics. The ever increasing use of neural networks as surrogates for physics-related problems calls for an improved understanding of boundary condition treatment, and its influence on the network accuracy. In this paper, several strategies to impose boundary conditions (namely padding, improved spatial context, and explicit encoding of physical boundaries) are investigated in the context of fully convolutional networks applied to recurrent tasks. These strategies are evaluated on two spatio-temporal evolving problems modeled by partial differential equations: the 2D propagation of acoustic waves (hyperbolic PDE) and the heat equation (parabolic PDE). Results reveal a high sensitivity of both accuracy and stability on the boundary implementation in such recurrent tasks. It is then demonstrated that the choice of the optimal padding strategy is directly linked to the data semantics. Furthermore, the inclusion of additional input spatial context or explicit physics-based rules allows a better handling of boundaries in particular for large number of recurrences, resulting in more robust and stable neural networks, while facilitating the design and versatility of such networks.

On the reproducibility of fully convolutional neural networks for modeling time-space evolving physical systems

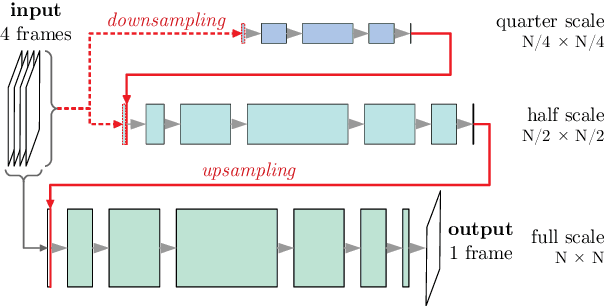
Reproducibility of a deep-learning fully convolutional neural network is evaluated by training several times the same network on identical conditions (database, hyperparameters, hardware) with non-deterministic Graphics Processings Unit (GPU) operations. The propagation of two-dimensional acoustic waves, typical of time-space evolving physical systems, is studied on both recursive and non-recursive tasks. Significant changes in models properties (weights, featured fields) are observed. When tested on various propagation benchmarks, these models systematically returned estimations with a high level of deviation, especially for the recurrent analysis which strongly amplifies variability due to the non-determinism. Trainings performed with double floating-point precision provide slightly better estimations and a significant reduction of the variability of both the network parameters and its testing error range.