Lionel Cheng
Medical Phrase Grounding with Region-Phrase Context Contrastive Alignment
Mar 14, 2023
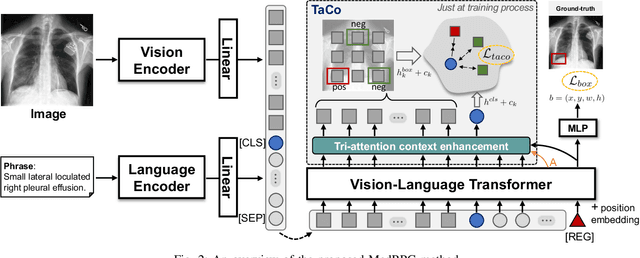
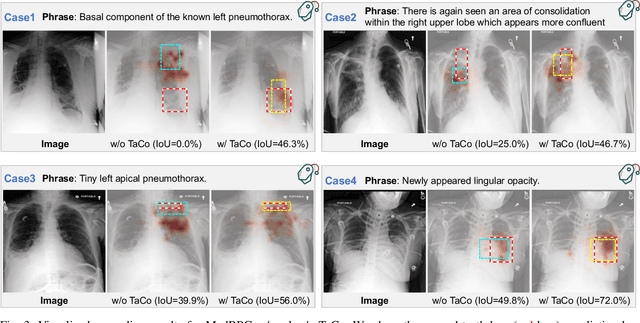
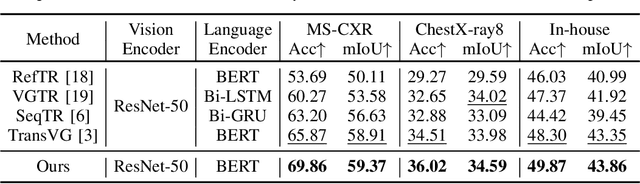
Abstract:Medical phrase grounding (MPG) aims to locate the most relevant region in a medical image, given a phrase query describing certain medical findings, which is an important task for medical image analysis and radiological diagnosis. However, existing visual grounding methods rely on general visual features for identifying objects in natural images and are not capable of capturing the subtle and specialized features of medical findings, leading to sub-optimal performance in MPG. In this paper, we propose MedRPG, an end-to-end approach for MPG. MedRPG is built on a lightweight vision-language transformer encoder and directly predicts the box coordinates of mentioned medical findings, which can be trained with limited medical data, making it a valuable tool in medical image analysis. To enable MedRPG to locate nuanced medical findings with better region-phrase correspondences, we further propose Tri-attention Context contrastive alignment (TaCo). TaCo seeks context alignment to pull both the features and attention outputs of relevant region-phrase pairs close together while pushing those of irrelevant regions far away. This ensures that the final box prediction depends more on its finding-specific regions and phrases. Experimental results on three MPG datasets demonstrate that our MedRPG outperforms state-of-the-art visual grounding approaches by a large margin. Additionally, the proposed TaCo strategy is effective in enhancing finding localization ability and reducing spurious region-phrase correlations.
Using neural networks to solve the 2D Poisson equation for electric field computation in plasma fluid simulations
Oct 04, 2021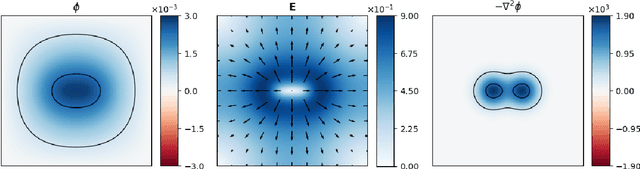
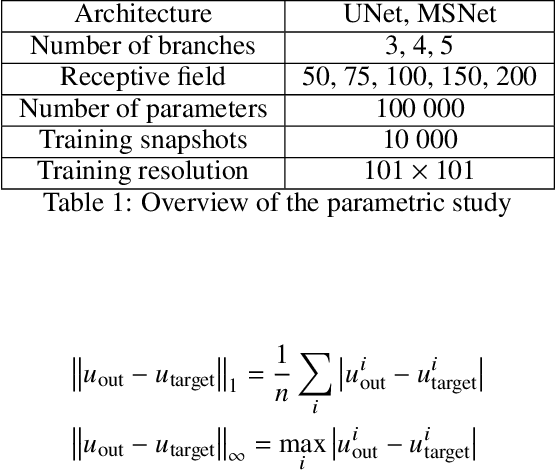
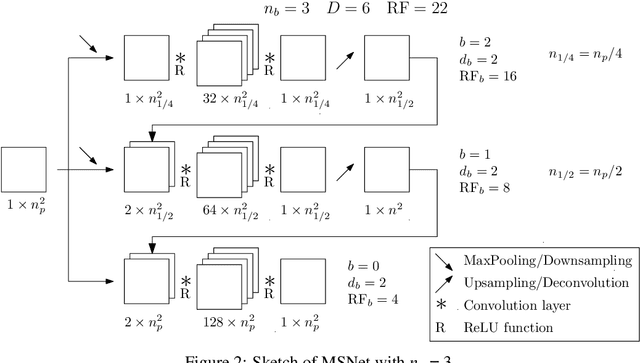
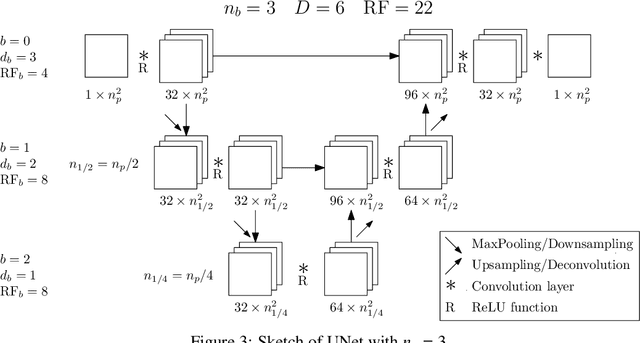
Abstract:The Poisson equation is critical to get a self-consistent solution in plasma fluid simulations used for Hall effect thrusters and streamers discharges. Solving the 2D Poisson equation with zero Dirichlet boundary conditions using a deep neural network is investigated using multiple-scale architectures, defined in terms of number of branches, depth and receptive field. The latter is found critical to correctly capture large topological structures of the field. The investigation of multiple architectures, losses, and hyperparameters provides an optimum network to solve accurately the steady Poisson problem. Generalization to new resolutions and domain sizes is then proposed using a proper scaling of the network. Finally, found neural network solver, called PlasmaNet, is coupled with an unsteady Euler plasma fluid equations solver. The test case corresponds to electron plasma oscillations which is used to assess the accuracy of the neural network solution in a time-dependent simulation. In this time-evolving problem, a physical loss is necessary to produce a stable simulation. PlasmaNet is then benchmarked on meshes with increasing number of nodes, and compared with an existing solver based on a standard linear system algorithm for the Poisson equation. It outperforms the classical plasma solver, up to speedups 700 times faster on large meshes. PlasmaNet is finally tested on a more complex case of discharge propagation involving chemistry and advection. The guidelines established in previous sections are applied to build the CNN to solve the same Poisson equation but in cylindrical coordinates. Results reveal good CNN predictions with significant speedup. These results pave the way to new computational strategies to predict unsteady problems involving a Poisson equation, including configurations with coupled multiphysics interactions such as in plasma flows.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge