Gradient-enhanced kriging for high-dimensional problems
Paper and Code
Aug 08, 2017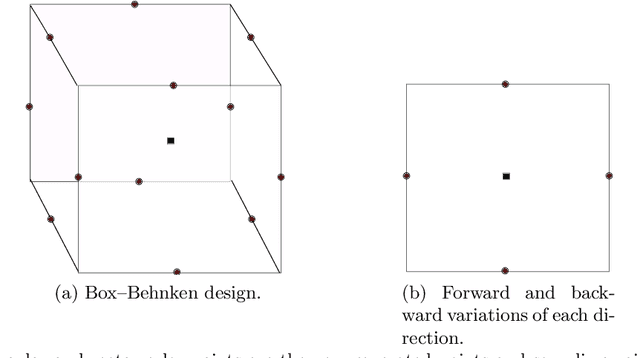
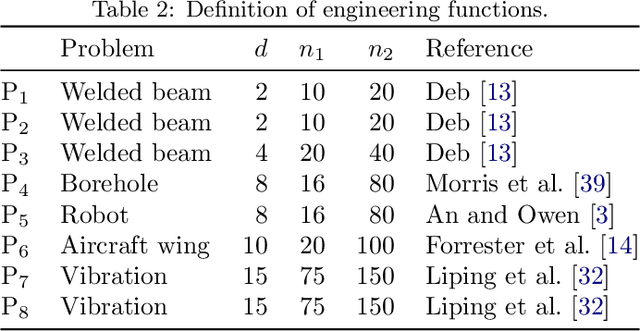
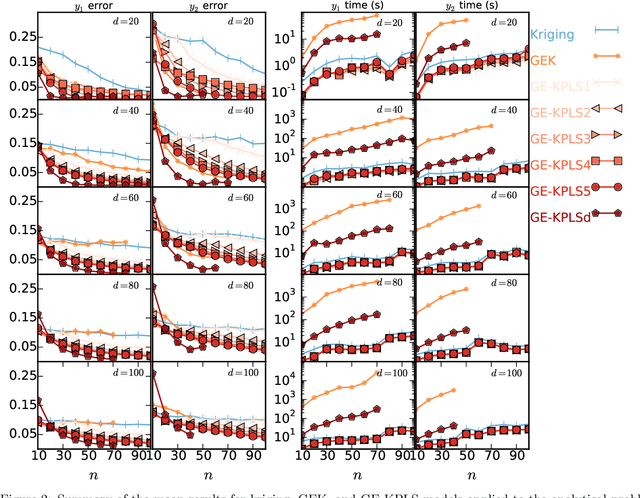
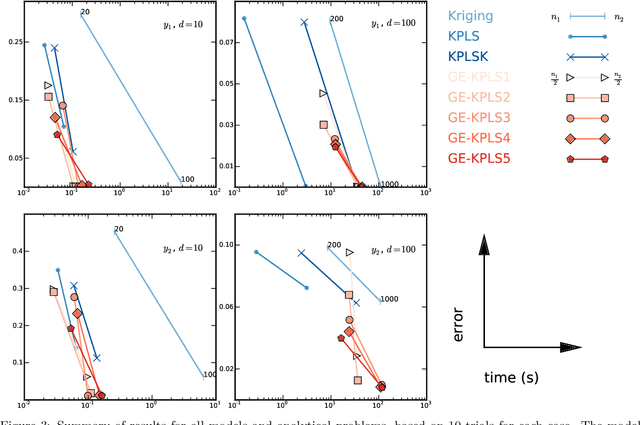
Surrogate models provide a low computational cost alternative to evaluating expensive functions. The construction of accurate surrogate models with large numbers of independent variables is currently prohibitive because it requires a large number of function evaluations. Gradient-enhanced kriging has the potential to reduce the number of function evaluations for the desired accuracy when efficient gradient computation, such as an adjoint method, is available. However, current gradient-enhanced kriging methods do not scale well with the number of sampling points due to the rapid growth in the size of the correlation matrix where new information is added for each sampling point in each direction of the design space. They do not scale well with the number of independent variables either due to the increase in the number of hyperparameters that needs to be estimated. To address this issue, we develop a new gradient-enhanced surrogate model approach that drastically reduced the number of hyperparameters through the use of the partial-least squares method that maintains accuracy. In addition, this method is able to control the size of the correlation matrix by adding only relevant points defined through the information provided by the partial-least squares method. To validate our method, we compare the global accuracy of the proposed method with conventional kriging surrogate models on two analytic functions with up to 100 dimensions, as well as engineering problems of varied complexity with up to 15 dimensions. We show that the proposed method requires fewer sampling points than conventional methods to obtain the desired accuracy, or provides more accuracy for a fixed budget of sampling points. In some cases, we get over 3 times more accurate models than a bench of surrogate models from the literature, and also over 3200 times faster than standard gradient-enhanced kriging models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge