Recursive querying of neural networks via weighted structures

Expressive querying of machine learning models - viewed as a form of intentional data - enables their verification and interpretation using declarative languages, thereby making learned representations of data more accessible. Motivated by the querying of feedforward neural networks, we investigate logics for weighted structures. In the absence of a bound on neural network depth, such logics must incorporate recursion; thereto we revisit the functional fixpoint mechanism proposed by Grädel and Gurevich. We adopt it in a Datalog-like syntax; we extend normal forms for fixpoint logics to weighted structures; and show an equivalent "loose" fixpoint mechanism that allows values of inductively defined weight functions to be overwritten. We propose a "scalar" restriction of functional fixpoint logic, of polynomial-time data complexity, and show it can express all PTIME model-agnostic queries over reduced networks with polynomially bounded weights. In contrast, we show that very simple model-agnostic queries are already NP-complete. Finally, we consider transformations of weighted structures by iterated transductions.

SQL4NN: Validation and expressive querying of models as data

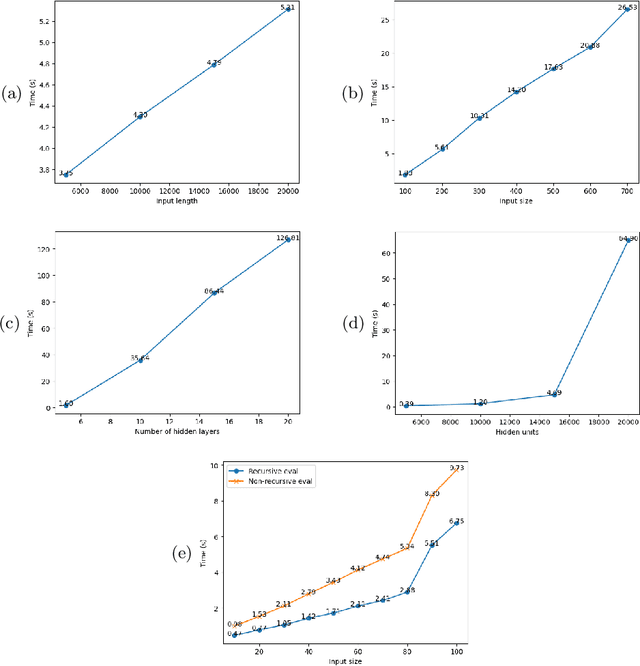
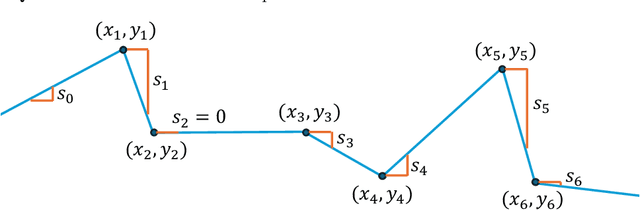
We consider machine learning models, learned from data, to be an important, intensional, kind of data in themselves. As such, various analysis tasks on models can be thought of as queries over this intensional data, often combined with extensional data such as data for training or validation. We demonstrate that relational database systems and SQL can actually be well suited for many such tasks.

Query languages for neural networks

We lay the foundations for a database-inspired approach to interpreting and understanding neural network models by querying them using declarative languages. Towards this end we study different query languages, based on first-order logic, that mainly differ in their access to the neural network model. First-order logic over the reals naturally yields a language which views the network as a black box; only the input--output function defined by the network can be queried. This is essentially the approach of constraint query languages. On the other hand, a white-box language can be obtained by viewing the network as a weighted graph, and extending first-order logic with summation over weight terms. The latter approach is essentially an abstraction of SQL. In general, the two approaches are incomparable in expressive power, as we will show. Under natural circumstances, however, the white-box approach can subsume the black-box approach; this is our main result. We prove the result concretely for linear constraint queries over real functions definable by feedforward neural networks with a fixed number of hidden layers and piecewise linear activation functions.