Jan Van den Bussche
Recursive querying of neural networks via weighted structures
Jan 06, 2026Abstract:Expressive querying of machine learning models - viewed as a form of intentional data - enables their verification and interpretation using declarative languages, thereby making learned representations of data more accessible. Motivated by the querying of feedforward neural networks, we investigate logics for weighted structures. In the absence of a bound on neural network depth, such logics must incorporate recursion; thereto we revisit the functional fixpoint mechanism proposed by Grädel and Gurevich. We adopt it in a Datalog-like syntax; we extend normal forms for fixpoint logics to weighted structures; and show an equivalent "loose" fixpoint mechanism that allows values of inductively defined weight functions to be overwritten. We propose a "scalar" restriction of functional fixpoint logic, of polynomial-time data complexity, and show it can express all PTIME model-agnostic queries over reduced networks with polynomially bounded weights. In contrast, we show that very simple model-agnostic queries are already NP-complete. Finally, we consider transformations of weighted structures by iterated transductions.
A Logical View of GNN-Style Computation and the Role of Activation Functions
Dec 22, 2025Abstract:We study the numerical and Boolean expressiveness of MPLang, a declarative language that captures the computation of graph neural networks (GNNs) through linear message passing and activation functions. We begin with A-MPLang, the fragment without activation functions, and give a characterization of its expressive power in terms of walk-summed features. For bounded activation functions, we show that (under mild conditions) all eventually constant activations yield the same expressive power - numerical and Boolean - and that it subsumes previously established logics for GNNs with eventually constant activation functions but without linear layers. Finally, we prove the first expressive separation between unbounded and bounded activations in the presence of linear layers: MPLang with ReLU is strictly more powerful for numerical queries than MPLang with eventually constant activation functions, e.g., truncated ReLU. This hinges on subtle interactions between linear aggregation and eventually constant non-linearities, and it establishes that GNNs using ReLU are more expressive than those restricted to eventually constant activations and linear layers.
Halting Recurrent GNNs and the Graded $μ$-Calculus
May 16, 2025Abstract:Graph Neural Networks (GNNs) are a class of machine-learning models that operate on graph-structured data. Their expressive power is intimately related to logics that are invariant under graded bisimilarity. Current proposals for recurrent GNNs either assume that the graph size is given to the model, or suffer from a lack of termination guarantees. In this paper, we propose a halting mechanism for recurrent GNNs. We prove that our halting model can express all node classifiers definable in graded modal mu-calculus, even for the standard GNN variant that is oblivious to the graph size. A recent breakthrough in the study of the expressivity of graded modal mu-calculus in the finite suggests that conversely, restricted to node classifiers definable in monadic second-order logic, recurrent GNNs can express only node classifiers definable in graded modal mu-calculus. To prove our main result, we develop a new approximate semantics for graded mu-calculus, which we believe to be of independent interest. We leverage this new semantics into a new model-checking algorithm, called the counting algorithm, which is oblivious to the graph size. In a final step we show that the counting algorithm can be implemented on a halting recurrent GNN.
SQL4NN: Validation and expressive querying of models as data
Feb 20, 2025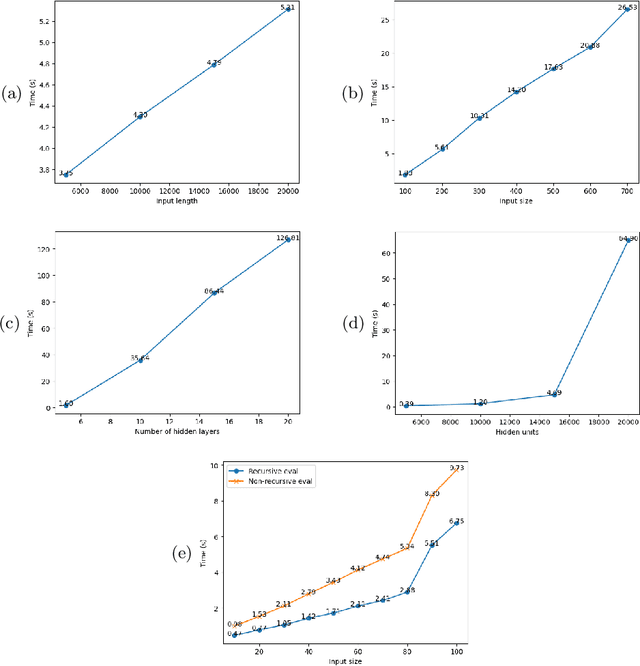
Abstract:We consider machine learning models, learned from data, to be an important, intensional, kind of data in themselves. As such, various analysis tasks on models can be thought of as queries over this intensional data, often combined with extensional data such as data for training or validation. We demonstrate that relational database systems and SQL can actually be well suited for many such tasks.
Query languages for neural networks
Aug 21, 2024Abstract:We lay the foundations for a database-inspired approach to interpreting and understanding neural network models by querying them using declarative languages. Towards this end we study different query languages, based on first-order logic, that mainly differ in their access to the neural network model. First-order logic over the reals naturally yields a language which views the network as a black box; only the input--output function defined by the network can be queried. This is essentially the approach of constraint query languages. On the other hand, a white-box language can be obtained by viewing the network as a weighted graph, and extending first-order logic with summation over weight terms. The latter approach is essentially an abstraction of SQL. In general, the two approaches are incomparable in expressive power, as we will show. Under natural circumstances, however, the white-box approach can subsume the black-box approach; this is our main result. We prove the result concretely for linear constraint queries over real functions definable by feedforward neural networks with a fixed number of hidden layers and piecewise linear activation functions.
Learning Graph Neural Networks using Exact Compression
Apr 28, 2023
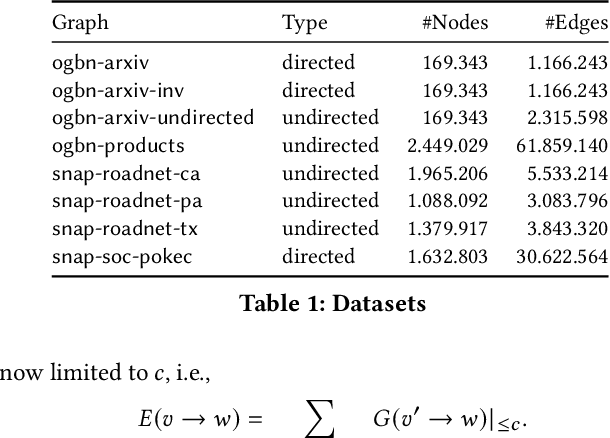
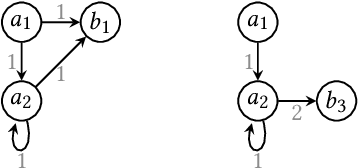
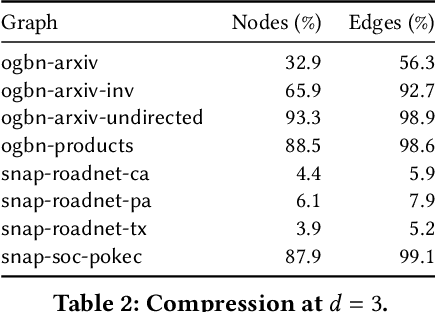
Abstract:Graph Neural Networks (GNNs) are a form of deep learning that enable a wide range of machine learning applications on graph-structured data. The learning of GNNs, however, is known to pose challenges for memory-constrained devices such as GPUs. In this paper, we study exact compression as a way to reduce the memory requirements of learning GNNs on large graphs. In particular, we adopt a formal approach to compression and propose a methodology that transforms GNN learning problems into provably equivalent compressed GNN learning problems. In a preliminary experimental evaluation, we give insights into the compression ratios that can be obtained on real-world graphs and apply our methodology to an existing GNN benchmark.
On the expressive power of message-passing neural networks as global feature map transformers
Mar 17, 2022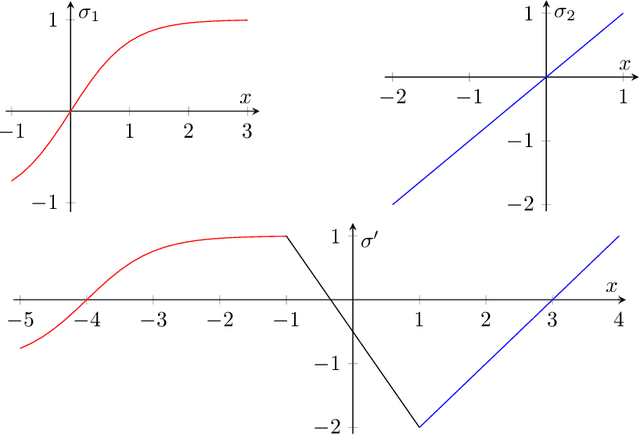
Abstract:We investigate the power of message-passing neural networks (MPNNs) in their capacity to transform the numerical features stored in the nodes of their input graphs. Our focus is on global expressive power, uniformly over all input graphs, or over graphs of bounded degree with features from a bounded domain. Accordingly, we introduce the notion of a global feature map transformer (GFMT). As a yardstick for expressiveness, we use a basic language for GFMTs, which we call MPLang. Every MPNN can be expressed in MPLang, and our results clarify to which extent the converse inclusion holds. We consider exact versus approximate expressiveness; the use of arbitrary activation functions; and the case where only the ReLU activation function is allowed.
Shape Fragments
Dec 22, 2021
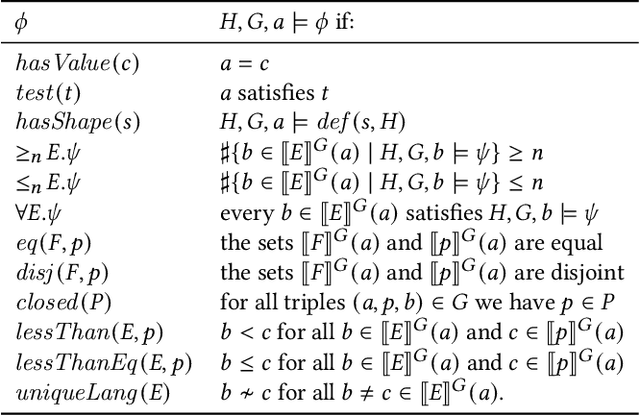

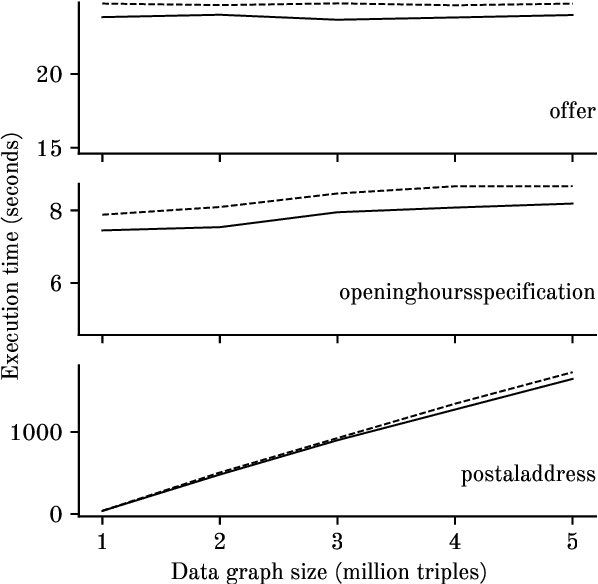
Abstract:In constraint languages for RDF graphs, such as ShEx and SHACL, constraints on nodes and their properties in RDF graphs are known as "shapes". Schemas in these languages list the various shapes that certain targeted nodes must satisfy for the graph to conform to the schema. Using SHACL, we propose in this paper a novel use of shapes, by which a set of shapes is used to extract a subgraph from an RDF graph, the so-called shape fragment. Our proposed mechanism fits in the framework of Linked Data Fragments. In this paper, (i) we define our extraction mechanism formally, building on recently proposed SHACL formalizations; (ii) we establish correctness properties, which relate shape fragments to notions of provenance for database queries; (iii) we compare shape fragments with SPARQL queries; (iv) we discuss implementation options; and (v) we present initial experiments demonstrating that shape fragments are a feasible new idea.
Learning with Value-Ramp
Apr 23, 2017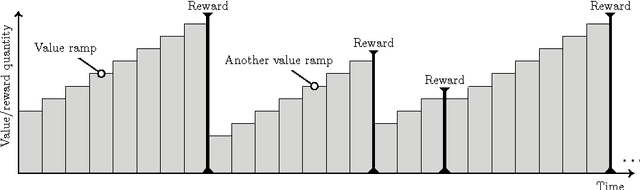
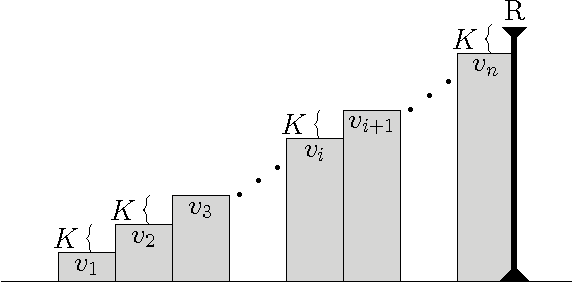
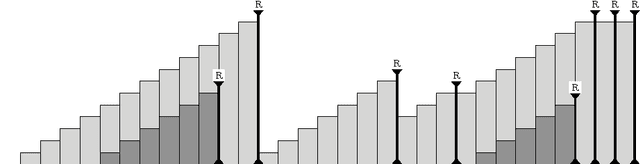
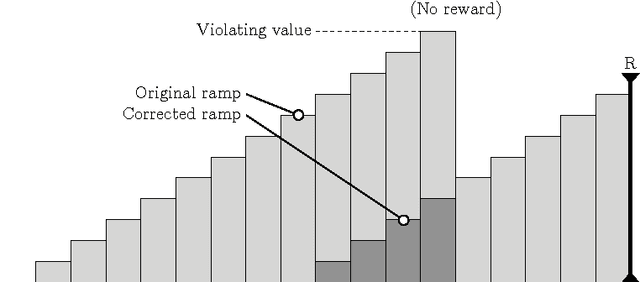
Abstract:We study a learning principle based on the intuition of forming ramps. The agent tries to follow an increasing sequence of values until the agent meets a peak of reward. The resulting Value-Ramp algorithm is natural, easy to configure, and has a robust implementation with natural numbers.
On the satisfiability problem for SPARQL patterns
Jun 01, 2016

Abstract:The satisfiability problem for SPARQL patterns is undecidable in general, since the expressive power of SPARQL 1.0 is comparable with that of the relational algebra. The goal of this paper is to delineate the boundary of decidability of satisfiability in terms of the constraints allowed in filter conditions. The classes of constraints considered are bound-constraints, negated bound-constraints, equalities, nonequalities, constant-equalities, and constant-nonequalities. The main result of the paper can be summarized by saying that, as soon as inconsistent filter conditions can be formed, satisfiability is undecidable. The key insight in each case is to find a way to emulate the set difference operation. Undecidability can then be obtained from a known undecidability result for the algebra of binary relations with union, composition, and set difference. When no inconsistent filter conditions can be formed, satisfiability is efficiently decidable by simple checks on bound variables and on the use of literals. The paper also points out that satisfiability for the so-called `well-designed' patterns can be decided by a check on bound variables and a check for inconsistent filter conditions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge