Learning with Value-Ramp

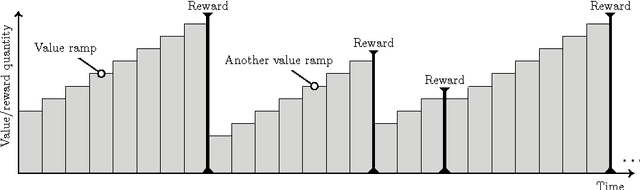
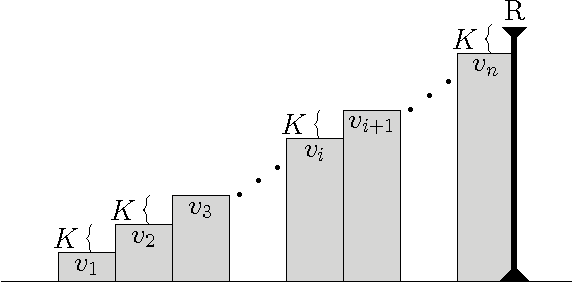
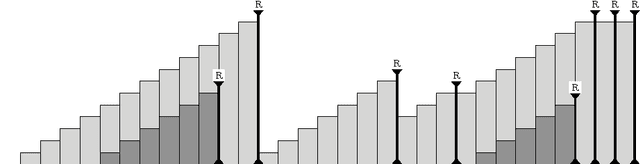
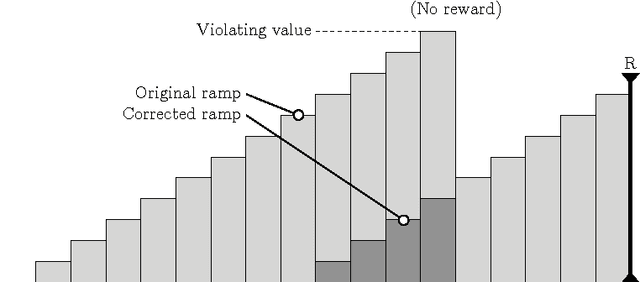
We study a learning principle based on the intuition of forming ramps. The agent tries to follow an increasing sequence of values until the agent meets a peak of reward. The resulting Value-Ramp algorithm is natural, easy to configure, and has a robust implementation with natural numbers.

On Avoidance Learning with Partial Observability

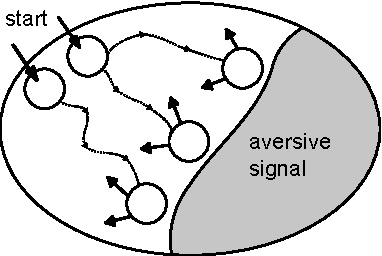
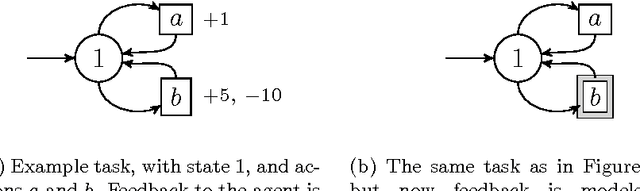
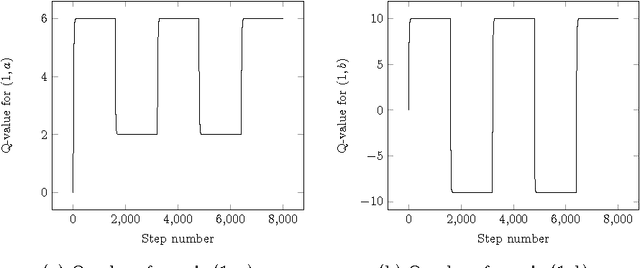
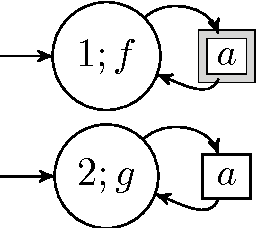
We study a framework where agents have to avoid aversive signals. The agents are given only partial information, in the form of features that are projections of task states. Additionally, the agents have to cope with non-determinism, defined as unpredictability on the way that actions are executed. The goal of each agent is to define its behavior based on feature-action pairs that reliably avoid aversive signals. We study a learning algorithm, called A-learning, that exhibits fixpoint convergence, where the belief of the allowed feature-action pairs eventually becomes fixed. A-learning is parameter-free and easy to implement.

On the convergence of cycle detection for navigational reinforcement learning

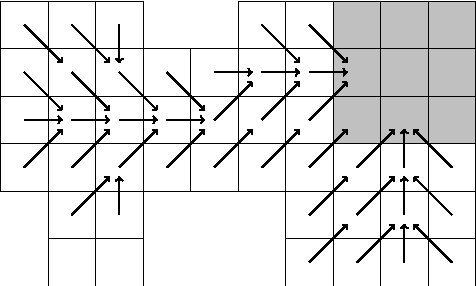
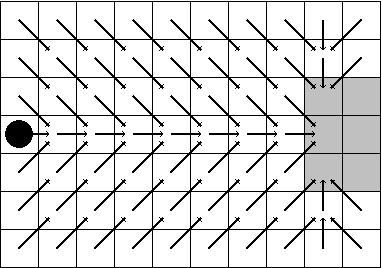
We consider a reinforcement learning framework where agents have to navigate from start states to goal states. We prove convergence of a cycle-detection learning algorithm on a class of tasks that we call reducible. Reducible tasks have an acyclic solution. We also syntactically characterize the form of the final policy. This characterization can be used to precisely detect the convergence point in a simulation. Our result demonstrates that even simple algorithms can be successful in learning a large class of nontrivial tasks. In addition, our framework is elementary in the sense that we only use basic concepts to formally prove convergence.

Positive Neural Networks in Discrete Time Implement Monotone-Regular Behaviors

We study the expressive power of positive neural networks. The model uses positive connection weights and multiple input neurons. Different behaviors can be expressed by varying the connection weights. We show that in discrete time, and in absence of noise, the class of positive neural networks captures the so-called monotone-regular behaviors, that are based on regular languages. A finer picture emerges if one takes into account the delay by which a monotone-regular behavior is implemented. Each monotone-regular behavior can be implemented by a positive neural network with a delay of one time unit. Some monotone-regular behaviors can be implemented with zero delay. And, interestingly, some simple monotone-regular behaviors can not be implemented with zero delay.