On the convergence of cycle detection for navigational reinforcement learning
Paper and Code
Jan 05, 2016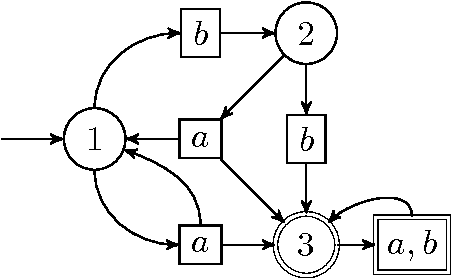
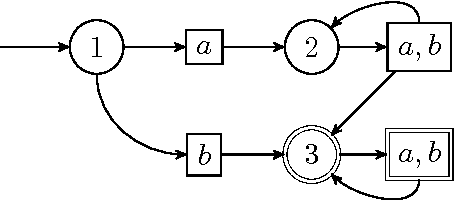
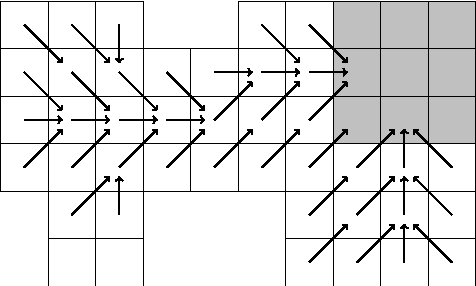
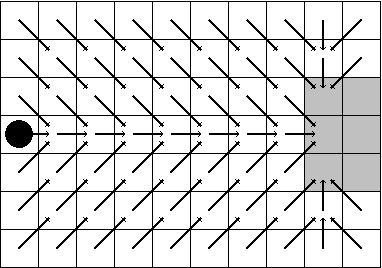
We consider a reinforcement learning framework where agents have to navigate from start states to goal states. We prove convergence of a cycle-detection learning algorithm on a class of tasks that we call reducible. Reducible tasks have an acyclic solution. We also syntactically characterize the form of the final policy. This characterization can be used to precisely detect the convergence point in a simulation. Our result demonstrates that even simple algorithms can be successful in learning a large class of nontrivial tasks. In addition, our framework is elementary in the sense that we only use basic concepts to formally prove convergence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge