Learning Graph Neural Networks using Exact Compression

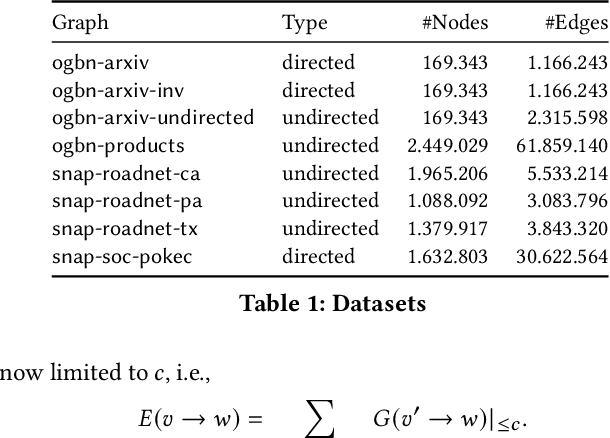
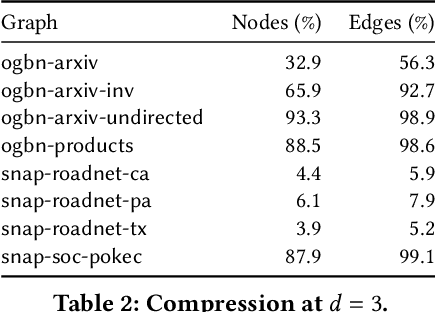
Graph Neural Networks (GNNs) are a form of deep learning that enable a wide range of machine learning applications on graph-structured data. The learning of GNNs, however, is known to pose challenges for memory-constrained devices such as GPUs. In this paper, we study exact compression as a way to reduce the memory requirements of learning GNNs on large graphs. In particular, we adopt a formal approach to compression and propose a methodology that transforms GNN learning problems into provably equivalent compressed GNN learning problems. In a preliminary experimental evaluation, we give insights into the compression ratios that can be obtained on real-world graphs and apply our methodology to an existing GNN benchmark.

On the expressive power of message-passing neural networks as global feature map transformers

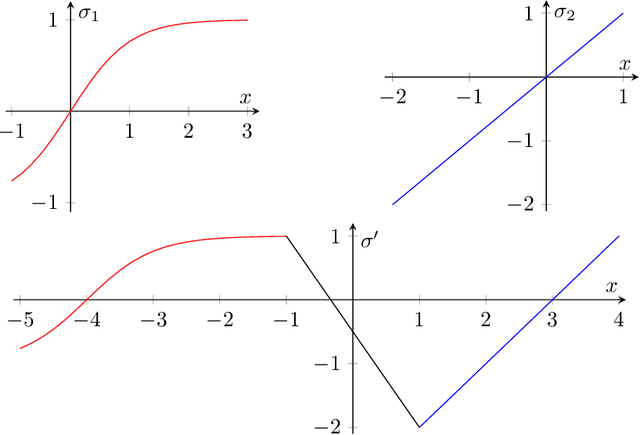
We investigate the power of message-passing neural networks (MPNNs) in their capacity to transform the numerical features stored in the nodes of their input graphs. Our focus is on global expressive power, uniformly over all input graphs, or over graphs of bounded degree with features from a bounded domain. Accordingly, we introduce the notion of a global feature map transformer (GFMT). As a yardstick for expressiveness, we use a basic language for GFMTs, which we call MPLang. Every MPNN can be expressed in MPLang, and our results clarify to which extent the converse inclusion holds. We consider exact versus approximate expressiveness; the use of arbitrary activation functions; and the case where only the ReLU activation function is allowed.