WILTing Trees: Interpreting the Distance Between MPNN Embeddings

We investigate the distance function learned by message passing neural networks (MPNNs) in specific tasks, aiming to capture the functional distance between prediction targets that MPNNs implicitly learn. This contrasts with previous work, which links MPNN distances on arbitrary tasks to structural distances on graphs that ignore task-specific information. To address this gap, we distill the distance between MPNN embeddings into an interpretable graph distance. Our method uses optimal transport on the Weisfeiler Leman Labeling Tree (WILT), where the edge weights reveal subgraphs that strongly influence the distance between embeddings. This approach generalizes two well-known graph kernels and can be computed in linear time. Through extensive experiments, we demonstrate that MPNNs define the relative position of embeddings by focusing on a small set of subgraphs that are known to be functionally important in the domain.

Towards Foundation Models on Graphs: An Analysis on Cross-Dataset Transfer of Pretrained GNNs

To develop a preliminary understanding towards Graph Foundation Models, we study the extent to which pretrained Graph Neural Networks can be applied across datasets, an effort requiring to be agnostic to dataset-specific features and their encodings. We build upon a purely structural pretraining approach and propose an extension to capture feature information while still being feature-agnostic. We evaluate pretrained models on downstream tasks for varying amounts of training samples and choices of pretraining datasets. Our preliminary results indicate that embeddings from pretrained models improve generalization only with enough downstream data points and in a degree which depends on the quantity and properties of pretraining data. Feature information can lead to improvements, but currently requires some similarities between pretraining and downstream feature spaces.

Logical Distillation of Graph Neural Networks

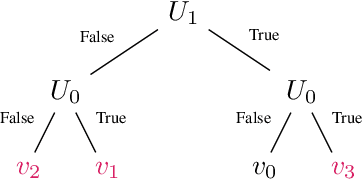
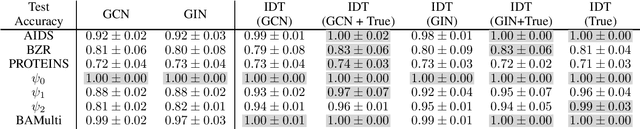
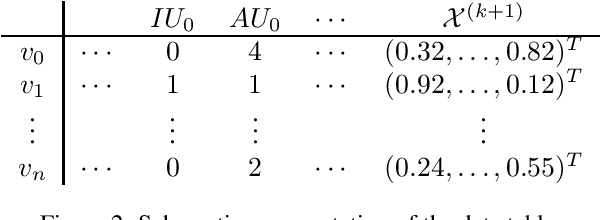
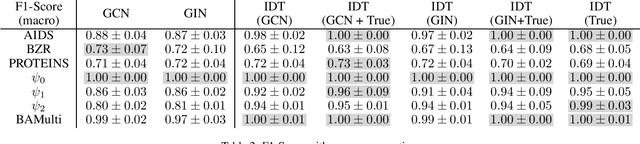
We present a logic based interpretable model for learning on graphs and an algorithm to distill this model from a Graph Neural Network (GNN). Recent results have shown connections between the expressivity of GNNs and the two-variable fragment of first-order logic with counting quantifiers (C2). We introduce a decision-tree based model which leverages an extension of C2 to distill interpretable logical classifiers from GNNs. We test our approach on multiple GNN architectures. The distilled models are interpretable, succinct, and attain similar accuracy to the underlying GNN. Furthermore, when the ground truth is expressible in C2, our approach outperforms the GNN.

On the Challenges and Opportunities in Generative AI

The field of deep generative modeling has grown rapidly and consistently over the years. With the availability of massive amounts of training data coupled with advances in scalable unsupervised learning paradigms, recent large-scale generative models show tremendous promise in synthesizing high-resolution images and text, as well as structured data such as videos and molecules. However, we argue that current large-scale generative AI models do not sufficiently address several fundamental issues that hinder their widespread adoption across domains. In this work, we aim to identify key unresolved challenges in modern generative AI paradigms that should be tackled to further enhance their capabilities, versatility, and reliability. By identifying these challenges, we aim to provide researchers with valuable insights for exploring fruitful research directions, thereby fostering the development of more robust and accessible generative AI solutions.

Expectation-Complete Graph Representations with Homomorphisms

We investigate novel random graph embeddings that can be computed in expected polynomial time and that are able to distinguish all non-isomorphic graphs in expectation. Previous graph embeddings have limited expressiveness and either cannot distinguish all graphs or cannot be computed efficiently for every graph. To be able to approximate arbitrary functions on graphs, we are interested in efficient alternatives that become arbitrarily expressive with increasing resources. Our approach is based on Lov\'asz' characterisation of graph isomorphism through an infinite dimensional vector of homomorphism counts. Our empirical evaluation shows competitive results on several benchmark graph learning tasks.

Corresponding Projections for Orphan Screening

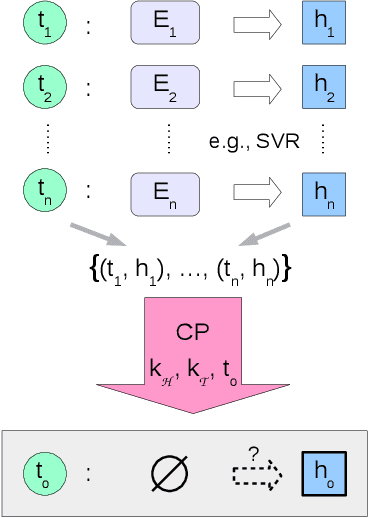
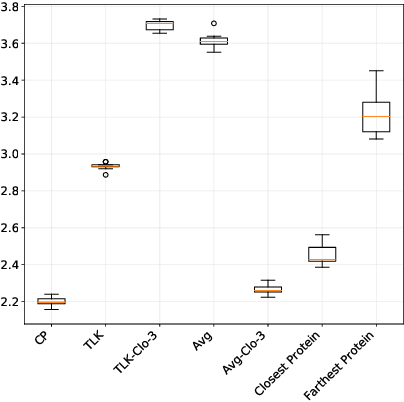
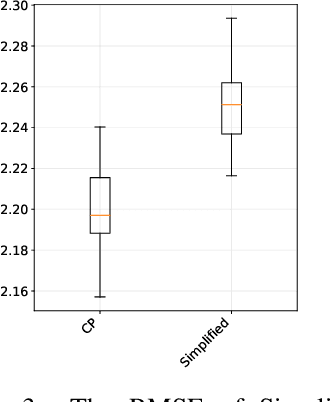
We propose a novel transfer learning approach for orphan screening called corresponding projections. In orphan screening the learning task is to predict the binding affinities of compounds to an orphan protein, i.e., one for which no training data is available. The identification of compounds with high affinity is a central concern in medicine since it can be used for drug discovery and design. Given a set of prediction models for proteins with labelled training data and a similarity between the proteins, corresponding projections constructs a model for the orphan protein from them such that the similarity between models resembles the one between proteins. Under the assumption that the similarity resemblance holds, we derive an efficient algorithm for kernel methods. We empirically show that the approach outperforms the state-of-the-art in orphan screening.

Effective Parallelisation for Machine Learning

We present a novel parallelisation scheme that simplifies the adaptation of learning algorithms to growing amounts of data as well as growing needs for accurate and confident predictions in critical applications. In contrast to other parallelisation techniques, it can be applied to a broad class of learning algorithms without further mathematical derivations and without writing dedicated code, while at the same time maintaining theoretical performance guarantees. Moreover, our parallelisation scheme is able to reduce the runtime of many learning algorithms to polylogarithmic time on quasi-polynomially many processing units. This is a significant step towards a general answer to an open question on the efficient parallelisation of machine learning algorithms in the sense of Nick's Class (NC). The cost of this parallelisation is in the form of a larger sample complexity. Our empirical study confirms the potential of our parallelisation scheme with fixed numbers of processors and instances in realistic application scenarios.

Large Scale Learning with Kreĭn Kernels

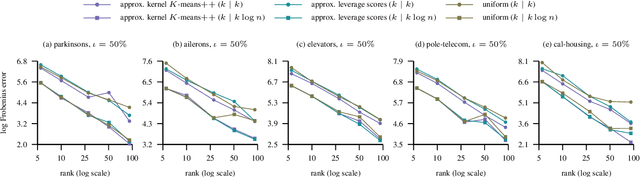
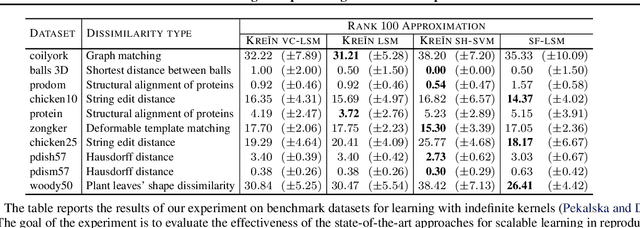
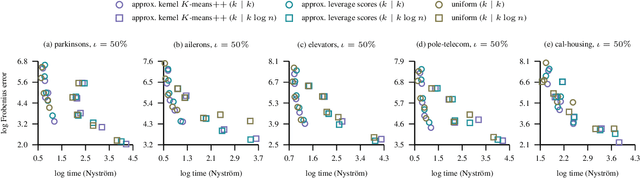
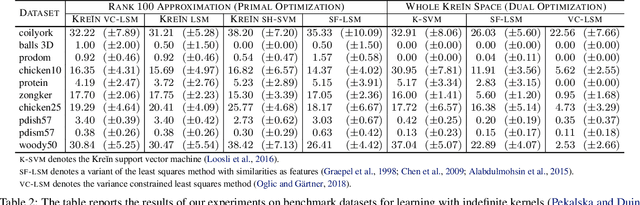
We extend the Nystr\"om method for low-rank approximation of positive definite Mercer kernels to approximation of indefinite kernel matrices. Our result is the first derivation of the approach that does not require the positive definiteness of the kernel function. Building on this result, we then devise highly scalable methods for learning in reproducing kernel Kre\u{\i}n spaces. The main motivation for our work comes from problems with structured representations (e.g., graphs, strings, time-series), where it is relatively easy to devise a pairwise (dis)similarity function based on intuition/knowledge of a domain expert. Such pairwise functions are typically not positive definite and it is often well beyond the expertise of practitioners to verify this condition. The proposed large scale approaches for learning in reproducing kernel Kre\u{\i}n spaces provide principled and theoretically well-founded means to tackle this class of problems. The effectiveness of the approaches is evaluated empirically using kernels defined on structured and vectorial data representations.