Large Scale Learning with Kreĭn Kernels

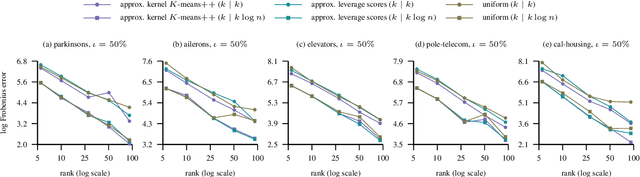
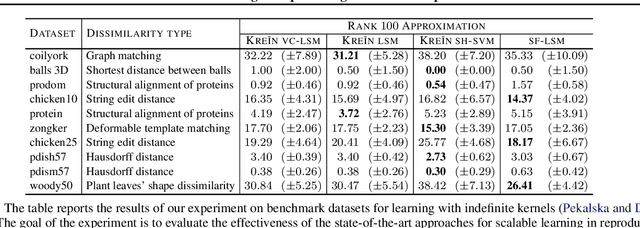
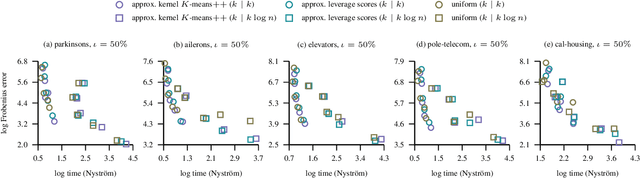
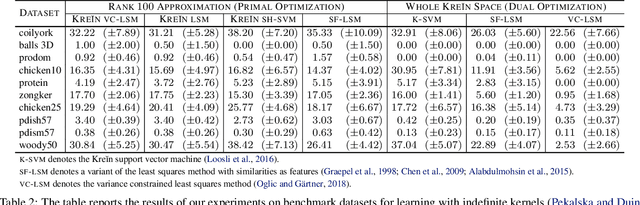
We extend the Nystr\"om method for low-rank approximation of positive definite Mercer kernels to approximation of indefinite kernel matrices. Our result is the first derivation of the approach that does not require the positive definiteness of the kernel function. Building on this result, we then devise highly scalable methods for learning in reproducing kernel Kre\u{\i}n spaces. The main motivation for our work comes from problems with structured representations (e.g., graphs, strings, time-series), where it is relatively easy to devise a pairwise (dis)similarity function based on intuition/knowledge of a domain expert. Such pairwise functions are typically not positive definite and it is often well beyond the expertise of practitioners to verify this condition. The proposed large scale approaches for learning in reproducing kernel Kre\u{\i}n spaces provide principled and theoretically well-founded means to tackle this class of problems. The effectiveness of the approaches is evaluated empirically using kernels defined on structured and vectorial data representations.