Dino Oglic
Segment Anyword: Mask Prompt Inversion for Open-Set Grounded Segmentation
May 23, 2025Abstract:Open-set image segmentation poses a significant challenge because existing methods often demand extensive training or fine-tuning and generally struggle to segment unified objects consistently across diverse text reference expressions. Motivated by this, we propose Segment Anyword, a novel training-free visual concept prompt learning approach for open-set language grounded segmentation that relies on token-level cross-attention maps from a frozen diffusion model to produce segmentation surrogates or mask prompts, which are then refined into targeted object masks. Initial prompts typically lack coherence and consistency as the complexity of the image-text increases, resulting in suboptimal mask fragments. To tackle this issue, we further introduce a novel linguistic-guided visual prompt regularization that binds and clusters visual prompts based on sentence dependency and syntactic structural information, enabling the extraction of robust, noise-tolerant mask prompts, and significant improvements in segmentation accuracy. The proposed approach is effective, generalizes across different open-set segmentation tasks, and achieves state-of-the-art results of 52.5 (+6.8 relative) mIoU on Pascal Context 59, 67.73 (+25.73 relative) cIoU on gRefCOCO, and 67.4 (+1.1 relative to fine-tuned methods) mIoU on GranDf, which is the most complex open-set grounded segmentation task in the field.
Masked Attention is All You Need for Graphs
Feb 16, 2024Abstract:Graph neural networks (GNNs) and variations of the message passing algorithm are the predominant means for learning on graphs, largely due to their flexibility, speed, and satisfactory performance. The design of powerful and general purpose GNNs, however, requires significant research efforts and often relies on handcrafted, carefully-chosen message passing operators. Motivated by this, we propose a remarkably simple alternative for learning on graphs that relies exclusively on attention. Graphs are represented as node or edge sets and their connectivity is enforced by masking the attention weight matrix, effectively creating custom attention patterns for each graph. Despite its simplicity, masked attention for graphs (MAG) has state-of-the-art performance on long-range tasks and outperforms strong message passing baselines and much more involved attention-based methods on over 55 node and graph-level tasks. We also show significantly better transfer learning capabilities compared to GNNs and comparable or better time and memory scaling. MAG has sub-linear memory scaling in the number of nodes or edges, enabling learning on dense graphs and future-proofing the approach.
Improving Antibody Humanness Prediction using Patent Data
Jan 31, 2024Abstract:We investigate the potential of patent data for improving the antibody humanness prediction using a multi-stage, multi-loss training process. Humanness serves as a proxy for the immunogenic response to antibody therapeutics, one of the major causes of attrition in drug discovery and a challenging obstacle for their use in clinical settings. We pose the initial learning stage as a weakly-supervised contrastive-learning problem, where each antibody sequence is associated with possibly multiple identifiers of function and the objective is to learn an encoder that groups them according to their patented properties. We then freeze a part of the contrastive encoder and continue training it on the patent data using the cross-entropy loss to predict the humanness score of a given antibody sequence. We illustrate the utility of the patent data and our approach by performing inference on three different immunogenicity datasets, unseen during training. Our empirical results demonstrate that the learned model consistently outperforms the alternative baselines and establishes new state-of-the-art on five out of six inference tasks, irrespective of the used metric.
Graph Neural Networks with Adaptive Readouts
Nov 09, 2022Abstract:An effective aggregation of node features into a graph-level representation via readout functions is an essential step in numerous learning tasks involving graph neural networks. Typically, readouts are simple and non-adaptive functions designed such that the resulting hypothesis space is permutation invariant. Prior work on deep sets indicates that such readouts might require complex node embeddings that can be difficult to learn via standard neighborhood aggregation schemes. Motivated by this, we investigate the potential of adaptive readouts given by neural networks that do not necessarily give rise to permutation invariant hypothesis spaces. We argue that in some problems such as binding affinity prediction where molecules are typically presented in a canonical form it might be possible to relax the constraints on permutation invariance of the hypothesis space and learn a more effective model of the affinity by employing an adaptive readout function. Our empirical results demonstrate the effectiveness of neural readouts on more than 40 datasets spanning different domains and graph characteristics. Moreover, we observe a consistent improvement over standard readouts (i.e., sum, max, and mean) relative to the number of neighborhood aggregation iterations and different convolutional operators.
Towards Robust Waveform-Based Acoustic Models
Oct 16, 2021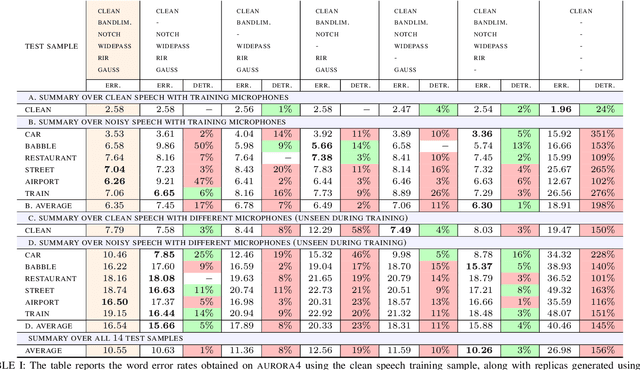
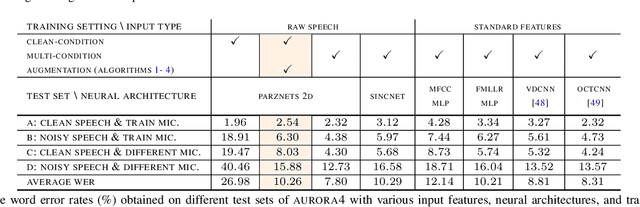
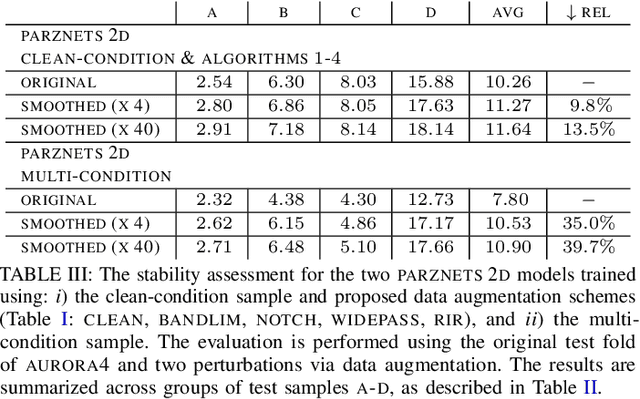
Abstract:We propose an approach for learning robust acoustic models in adverse environments, characterized by a significant mismatch between training and test conditions. This problem is of paramount importance for the deployment of speech recognition systems that need to perform well in unseen environments. Our approach is an instance of vicinal risk minimization, which aims to improve risk estimates during training by replacing the delta functions that define the empirical density over the input space with an approximation of the marginal population density in the vicinity of the training samples. More specifically, we assume that local neighborhoods centered at training samples can be approximated using a mixture of Gaussians, and demonstrate theoretically that this can incorporate robust inductive bias into the learning process. We characterize the individual mixture components implicitly via data augmentation schemes, designed to address common sources of spurious correlations in acoustic models. To avoid potential confounding effects on robustness due to information loss, which has been associated with standard feature extraction techniques (e.g., FBANK and MFCC features), we focus our evaluation on the waveform-based setting. Our empirical results show that the proposed approach can generalize to unseen noise conditions, with 150% relative improvement in out-of-distribution generalization compared to training using the standard risk minimization principle. Moreover, the results demonstrate competitive performance relative to models learned using a training sample designed to match the acoustic conditions characteristic of test utterances (i.e., optimal vicinal densities).
Parzen Filters for Spectral Decomposition of Signals
Jun 23, 2019

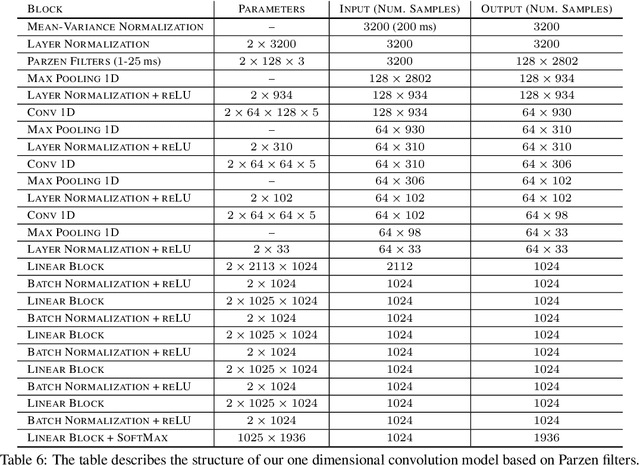
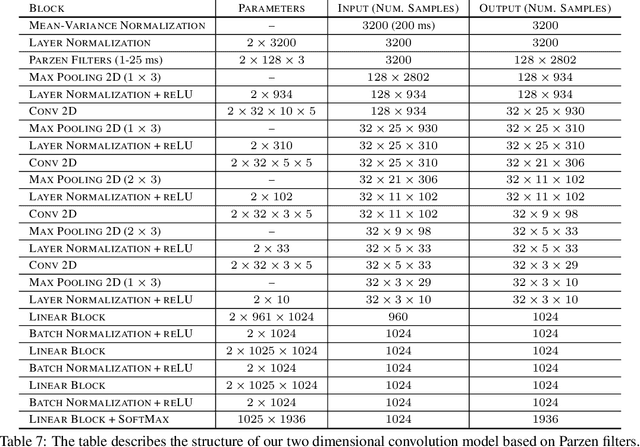
Abstract:We propose a novel family of band-pass filters for efficient spectral decomposition of signals. Previous work has already established the effectiveness of representations based on static band-pass filtering of speech signals (e.g., mel-frequency cepstral coefficients and deep scattering spectrum). A potential shortcoming of these approaches is the fact that the parameters specifying such a representation are fixed a priori and not learned using the available data. To address this limitation, we propose a family of filters defined via cosine modulations of Parzen windows, where the modulation frequency models the center of a spectral band-pass filter and the length of a Parzen window is inversely proportional to the filter width in the spectral domain. We propose to learn such a representation using stochastic variational Bayesian inference based on Gaussian dropout posteriors and sparsity inducing priors. Such a prior leads to an intractable integral defining the Kullback--Leibler divergence term for which we propose an effective approximation based on the Gauss--Hermite quadrature. Our empirical results demonstrate that the proposed approach is competitive with state-of-the-art models on speech recognition tasks.
Large Scale Learning with Kreĭn Kernels
Sep 06, 2018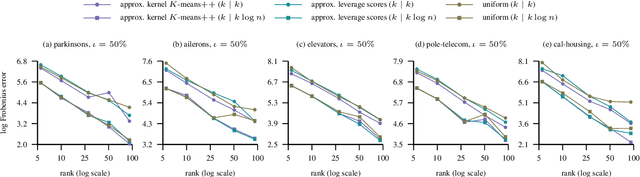
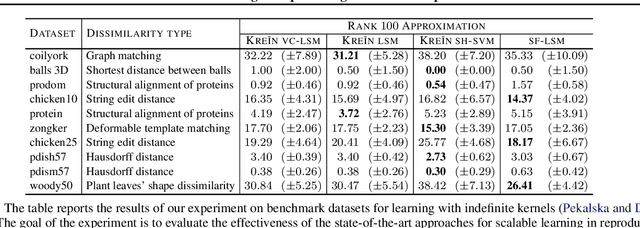
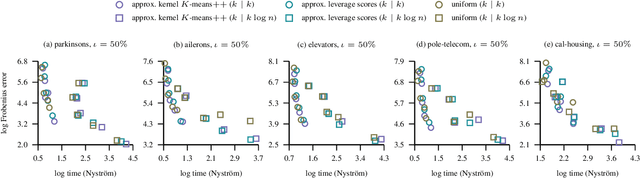
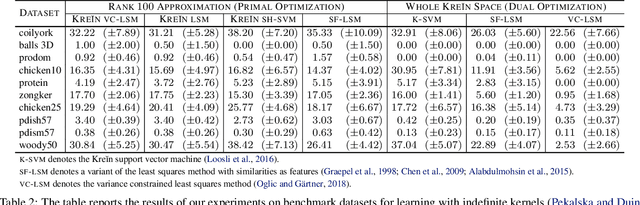
Abstract:We extend the Nystr\"om method for low-rank approximation of positive definite Mercer kernels to approximation of indefinite kernel matrices. Our result is the first derivation of the approach that does not require the positive definiteness of the kernel function. Building on this result, we then devise highly scalable methods for learning in reproducing kernel Kre\u{\i}n spaces. The main motivation for our work comes from problems with structured representations (e.g., graphs, strings, time-series), where it is relatively easy to devise a pairwise (dis)similarity function based on intuition/knowledge of a domain expert. Such pairwise functions are typically not positive definite and it is often well beyond the expertise of practitioners to verify this condition. The proposed large scale approaches for learning in reproducing kernel Kre\u{\i}n spaces provide principled and theoretically well-founded means to tackle this class of problems. The effectiveness of the approaches is evaluated empirically using kernels defined on structured and vectorial data representations.
A Unified Analysis of Random Fourier Features
Jun 24, 2018

Abstract:We provide the first unified theoretical analysis of supervised learning with random Fourier features, covering different types of loss functions characteristic to kernel methods developed for this setting. More specifically, we investigate learning with squared error and Lipschitz continuous loss functions and give the sharpest expected risk convergence rates for problems in which random Fourier features are sampled either using the spectral measure corresponding to a shift-invariant kernel or the ridge leverage score function proposed in~\cite{avron2017random}. The trade-off between the number of features and the expected risk convergence rate is expressed in terms of the regularization parameter and the effective dimension of the problem. While the former can effectively capture the complexity of the target hypothesis, the latter is known for expressing the fine structure of the kernel with respect to the marginal distribution of a data generating process~\cite{caponnetto2007optimal}. In addition to our theoretical results, we propose an approximate leverage score sampler for large scale problems and show that it can be significantly more effective than the spectral measure sampler.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge