Towards Robust Waveform-Based Acoustic Models

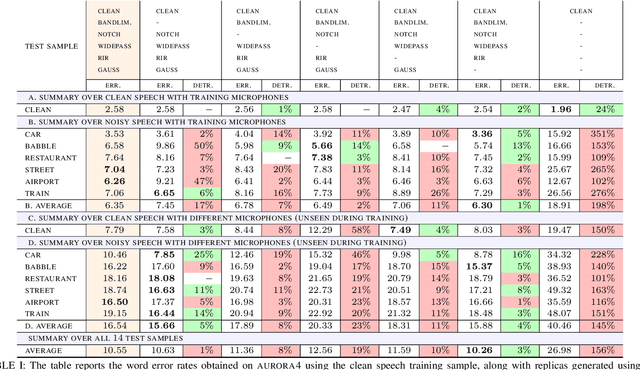
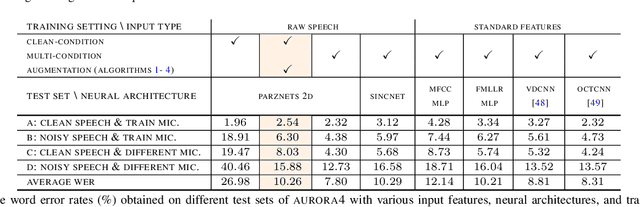
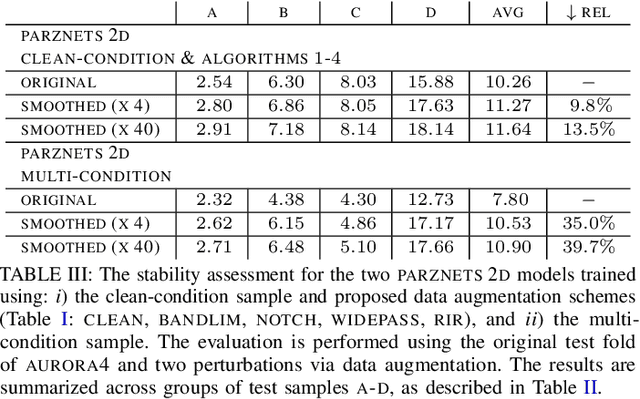
We propose an approach for learning robust acoustic models in adverse environments, characterized by a significant mismatch between training and test conditions. This problem is of paramount importance for the deployment of speech recognition systems that need to perform well in unseen environments. Our approach is an instance of vicinal risk minimization, which aims to improve risk estimates during training by replacing the delta functions that define the empirical density over the input space with an approximation of the marginal population density in the vicinity of the training samples. More specifically, we assume that local neighborhoods centered at training samples can be approximated using a mixture of Gaussians, and demonstrate theoretically that this can incorporate robust inductive bias into the learning process. We characterize the individual mixture components implicitly via data augmentation schemes, designed to address common sources of spurious correlations in acoustic models. To avoid potential confounding effects on robustness due to information loss, which has been associated with standard feature extraction techniques (e.g., FBANK and MFCC features), we focus our evaluation on the waveform-based setting. Our empirical results show that the proposed approach can generalize to unseen noise conditions, with 150% relative improvement in out-of-distribution generalization compared to training using the standard risk minimization principle. Moreover, the results demonstrate competitive performance relative to models learned using a training sample designed to match the acoustic conditions characteristic of test utterances (i.e., optimal vicinal densities).

Parzen Filters for Spectral Decomposition of Signals

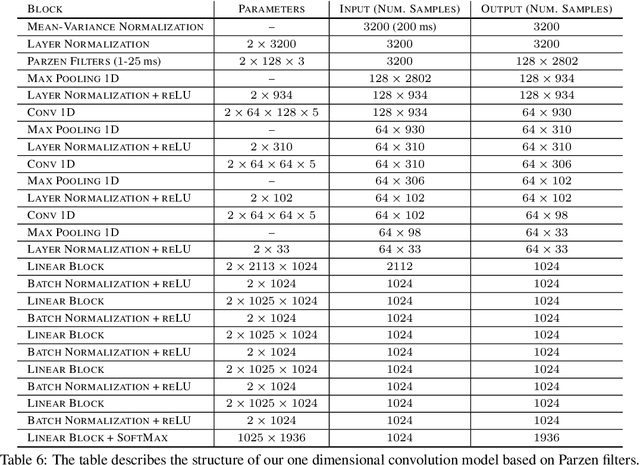
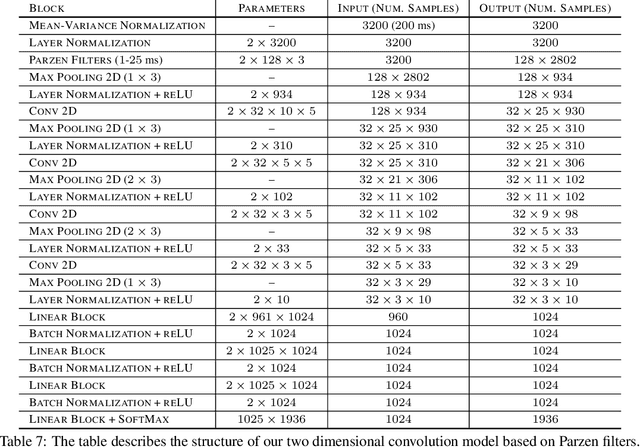
We propose a novel family of band-pass filters for efficient spectral decomposition of signals. Previous work has already established the effectiveness of representations based on static band-pass filtering of speech signals (e.g., mel-frequency cepstral coefficients and deep scattering spectrum). A potential shortcoming of these approaches is the fact that the parameters specifying such a representation are fixed a priori and not learned using the available data. To address this limitation, we propose a family of filters defined via cosine modulations of Parzen windows, where the modulation frequency models the center of a spectral band-pass filter and the length of a Parzen window is inversely proportional to the filter width in the spectral domain. We propose to learn such a representation using stochastic variational Bayesian inference based on Gaussian dropout posteriors and sparsity inducing priors. Such a prior leads to an intractable integral defining the Kullback--Leibler divergence term for which we propose an effective approximation based on the Gauss--Hermite quadrature. Our empirical results demonstrate that the proposed approach is competitive with state-of-the-art models on speech recognition tasks.

Phase transitions in Restricted Boltzmann Machines with generic priors

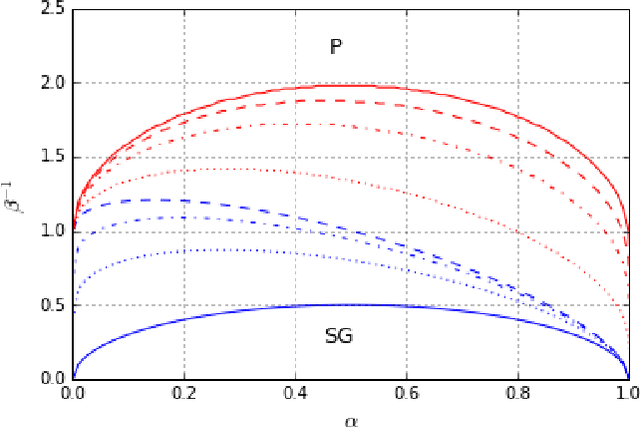
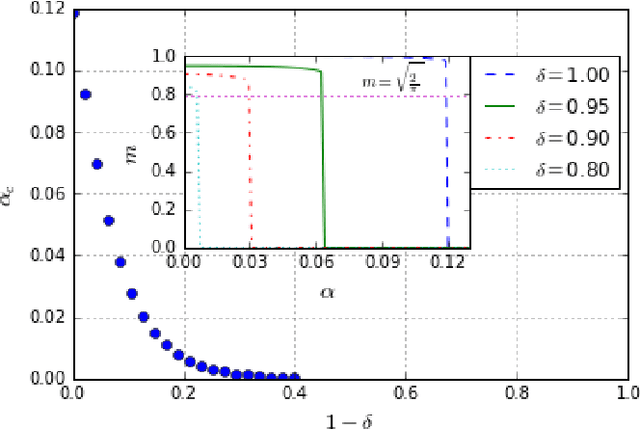
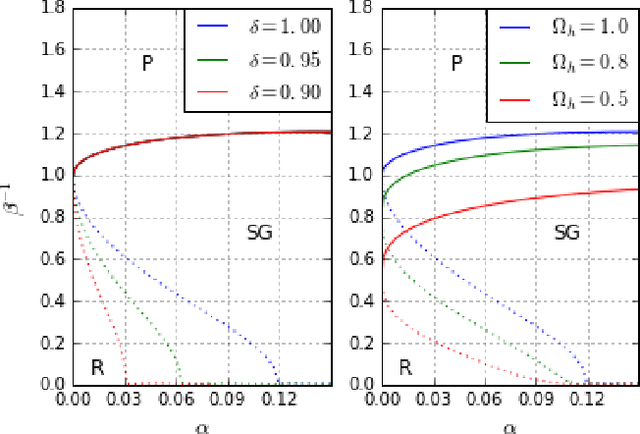
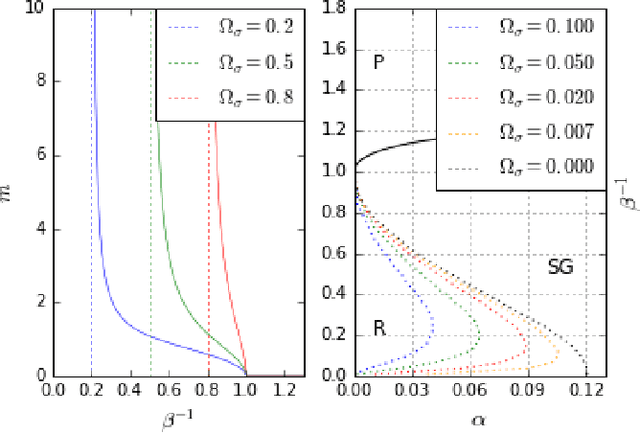
We study Generalised Restricted Boltzmann Machines with generic priors for units and weights, interpolating between Boolean and Gaussian variables. We present a complete analysis of the replica symmetric phase diagram of these systems, which can be regarded as Generalised Hopfield models. We underline the role of the retrieval phase for both inference and learning processes and we show that retrieval is robust for a large class of weight and unit priors, beyond the standard Hopfield scenario. Furthermore we show how the paramagnetic phase boundary is directly related to the optimal size of the training set necessary for good generalisation in a teacher-student scenario of unsupervised learning.

Phase Diagram of Restricted Boltzmann Machines and Generalised Hopfield Networks with Arbitrary Priors

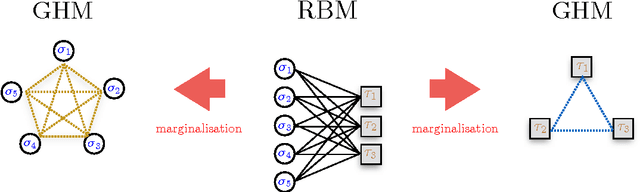
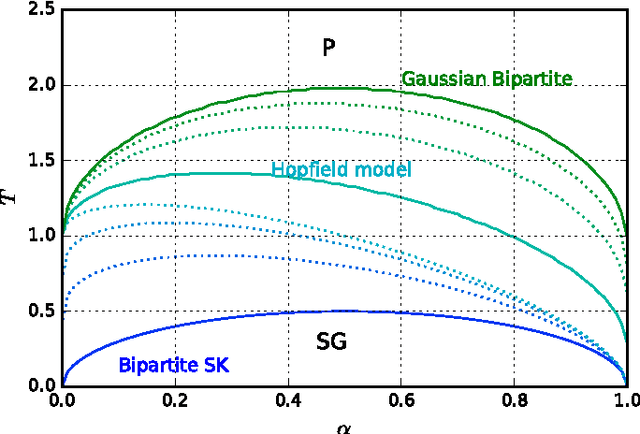
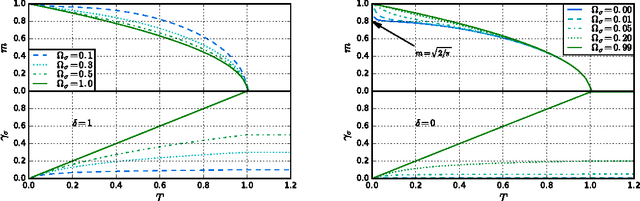
Restricted Boltzmann Machines are described by the Gibbs measure of a bipartite spin glass, which in turn corresponds to the one of a generalised Hopfield network. This equivalence allows us to characterise the state of these systems in terms of retrieval capabilities, both at low and high load. We study the paramagnetic-spin glass and the spin glass-retrieval phase transitions, as the pattern (i.e. weight) distribution and spin (i.e. unit) priors vary smoothly from Gaussian real variables to Boolean discrete variables. Our analysis shows that the presence of a retrieval phase is robust and not peculiar to the standard Hopfield model with Boolean patterns. The retrieval region is larger when the pattern entries and retrieval units get more peaked and, conversely, when the hidden units acquire a broader prior and therefore have a stronger response to high fields. Moreover, at low load retrieval always exists below some critical temperature, for every pattern distribution ranging from the Boolean to the Gaussian case.

Dynamical selection of Nash equilibria using Experience Weighted Attraction Learning: emergence of heterogeneous mixed equilibria

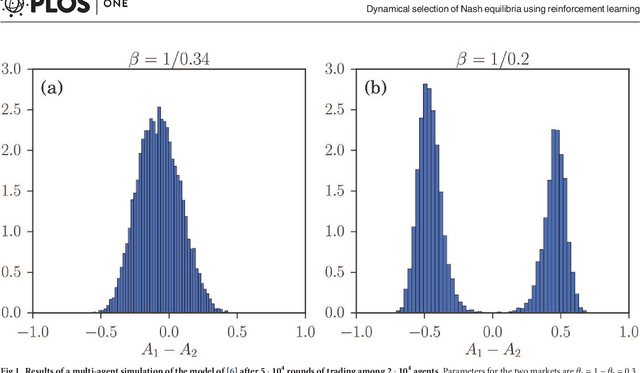
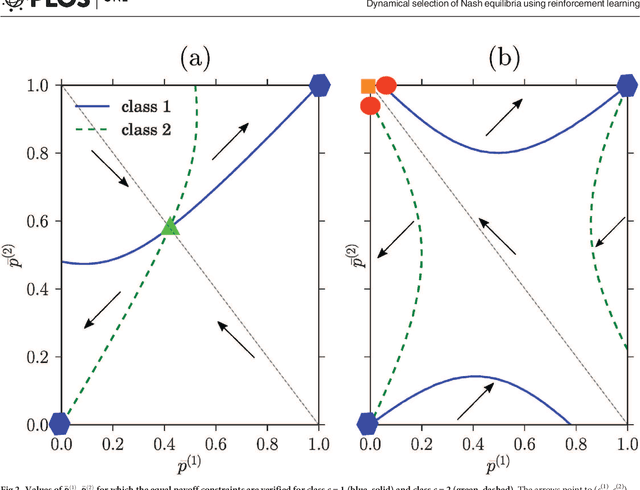
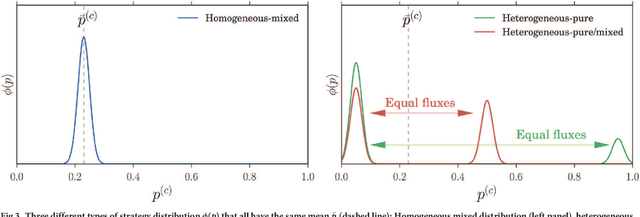
We study the distribution of strategies in a large game that models how agents choose among different double auction markets. We classify the possible mean field Nash equilibria, which include potentially segregated states where an agent population can split into subpopulations adopting different strategies. As the game is aggregative, the actual equilibrium strategy distributions remain undetermined, however. We therefore compare with the results of Experience-Weighted Attraction (EWA) learning, which at long times leads to Nash equilibria in the appropriate limits of large intensity of choice, low noise (long agent memory) and perfect imputation of missing scores (fictitious play). The learning dynamics breaks the indeterminacy of the Nash equilibria. Non-trivially, depending on how the relevant limits are taken, more than one type of equilibrium can be selected. These include the standard homogeneous mixed and heterogeneous pure states, but also \emph{heterogeneous mixed} states where different agents play different strategies that are not all pure. The analysis of the EWA learning involves Fokker-Planck modeling combined with large deviation methods. The theoretical results are confirmed by multi-agent simulations.

Speech Recognition Front End Without Information Loss

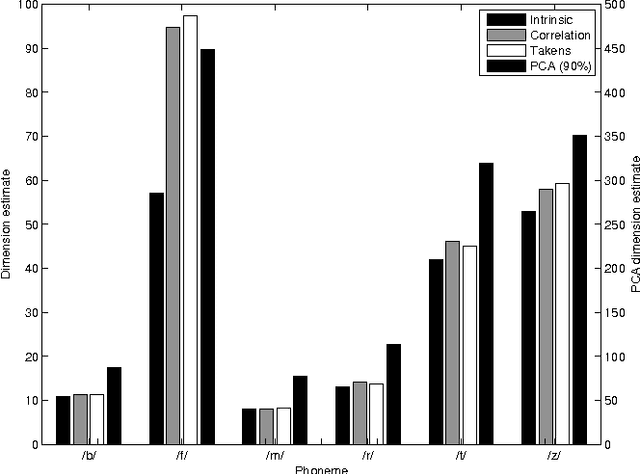
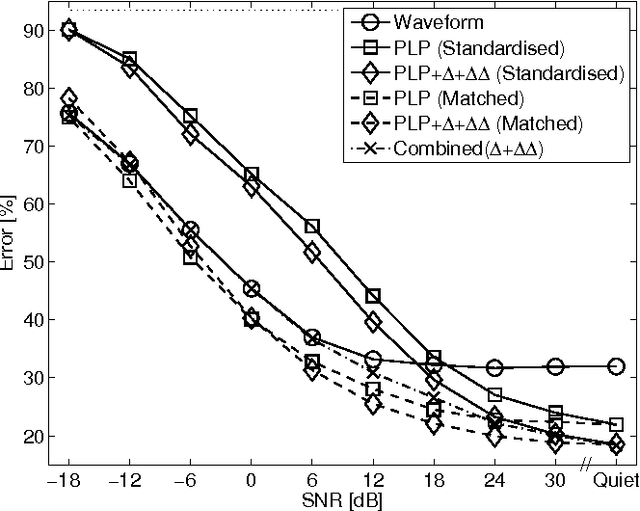
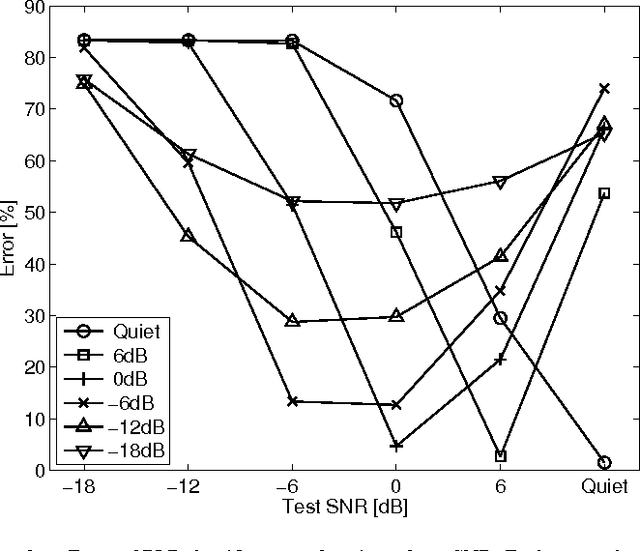
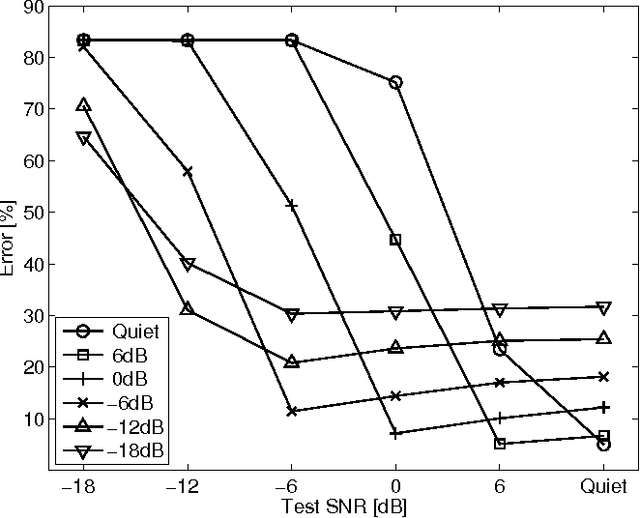
Speech representation and modelling in high-dimensional spaces of acoustic waveforms, or a linear transformation thereof, is investigated with the aim of improving the robustness of automatic speech recognition to additive noise. The motivation behind this approach is twofold: (i) the information in acoustic waveforms that is usually removed in the process of extracting low-dimensional features might aid robust recognition by virtue of structured redundancy analogous to channel coding, (ii) linear feature domains allow for exact noise adaptation, as opposed to representations that involve non-linear processing which makes noise adaptation challenging. Thus, we develop a generative framework for phoneme modelling in high-dimensional linear feature domains, and use it in phoneme classification and recognition tasks. Results show that classification and recognition in this framework perform better than analogous PLP and MFCC classifiers below 18 dB SNR. A combination of the high-dimensional and MFCC features at the likelihood level performs uniformly better than either of the individual representations across all noise levels.

A Subband-Based SVM Front-End for Robust ASR

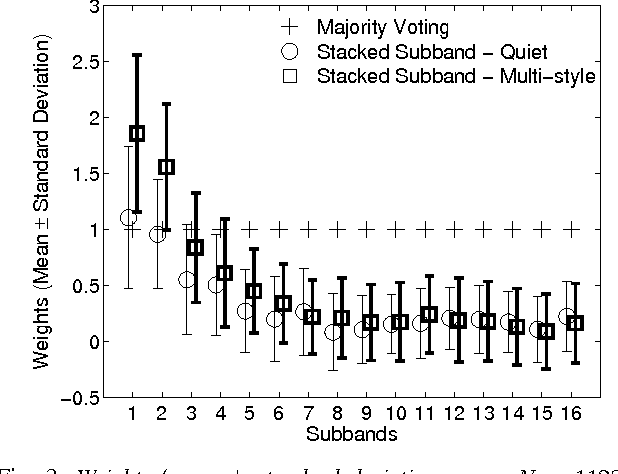
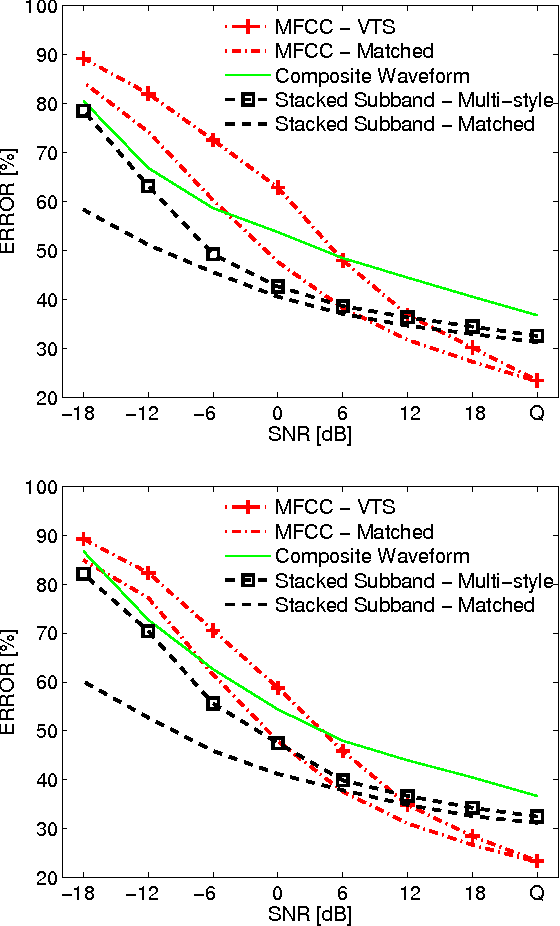
This work proposes a novel support vector machine (SVM) based robust automatic speech recognition (ASR) front-end that operates on an ensemble of the subband components of high-dimensional acoustic waveforms. The key issues of selecting the appropriate SVM kernels for classification in frequency subbands and the combination of individual subband classifiers using ensemble methods are addressed. The proposed front-end is compared with state-of-the-art ASR front-ends in terms of robustness to additive noise and linear filtering. Experiments performed on the TIMIT phoneme classification task demonstrate the benefits of the proposed subband based SVM front-end: it outperforms the standard cepstral front-end in the presence of noise and linear filtering for signal-to-noise ratio (SNR) below 12-dB. A combination of the proposed front-end with a conventional front-end such as MFCC yields further improvements over the individual front ends across the full range of noise levels.

Random walk kernels and learning curves for Gaussian process regression on random graphs

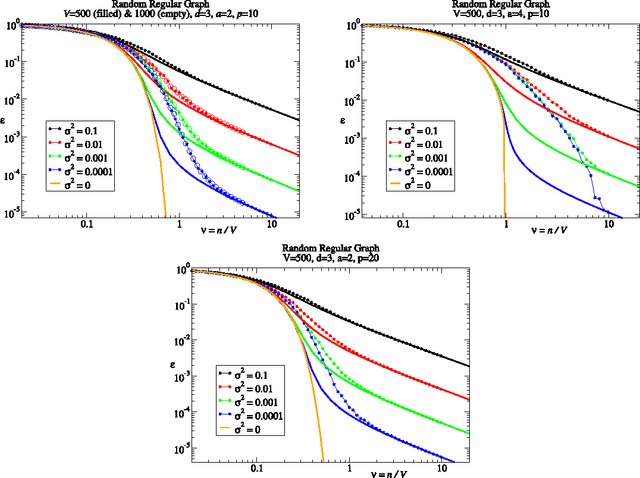
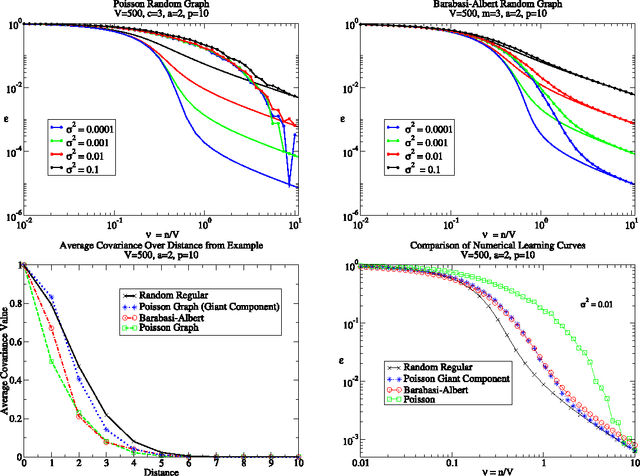
We consider learning on graphs, guided by kernels that encode similarity between vertices. Our focus is on random walk kernels, the analogues of squared exponential kernels in Euclidean spaces. We show that on large, locally treelike, graphs these have some counter-intuitive properties, specifically in the limit of large kernel lengthscales. We consider using these kernels as covariance matrices of e.g.\ Gaussian processes (GPs). In this situation one typically scales the prior globally to normalise the average of the prior variance across vertices. We demonstrate that, in contrast to the Euclidean case, this generically leads to significant variation in the prior variance across vertices, which is undesirable from the probabilistic modelling point of view. We suggest the random walk kernel should be normalised locally, so that each vertex has the same prior variance, and analyse the consequences of this by studying learning curves for Gaussian process regression. Numerical calculations as well as novel theoretical predictions for the learning curves using belief propagation make it clear that one obtains distinctly different probabilistic models depending on the choice of normalisation. Our method for predicting the learning curves using belief propagation is significantly more accurate than previous approximations and should become exact in the limit of large random graphs.

Replica theory for learning curves for Gaussian processes on random graphs

Statistical physics approaches can be used to derive accurate predictions for the performance of inference methods learning from potentially noisy data, as quantified by the learning curve defined as the average error versus number of training examples. We analyse a challenging problem in the area of non-parametric inference where an effectively infinite number of parameters has to be learned, specifically Gaussian process regression. When the inputs are vertices on a random graph and the outputs noisy function values, we show that replica techniques can be used to obtain exact performance predictions in the limit of large graphs. The covariance of the Gaussian process prior is defined by a random walk kernel, the discrete analogue of squared exponential kernels on continuous spaces. Conventionally this kernel is normalised only globally, so that the prior variance can differ between vertices; as a more principled alternative we consider local normalisation, where the prior variance is uniform.

Learning curves for multi-task Gaussian process regression

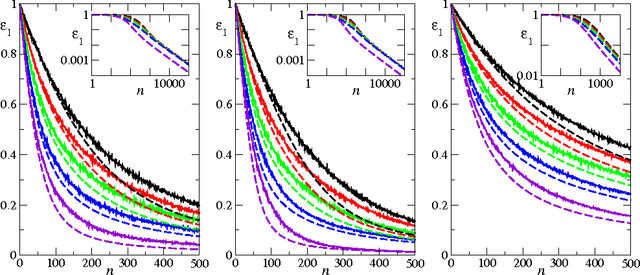
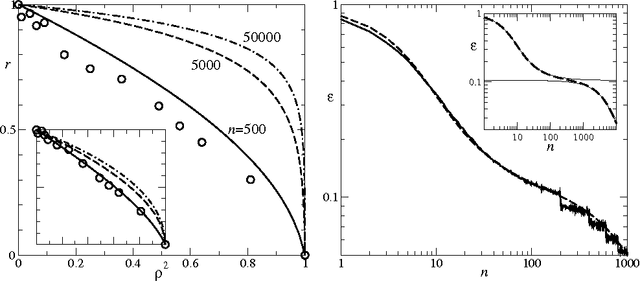
We study the average case performance of multi-task Gaussian process (GP) regression as captured in the learning curve, i.e. the average Bayes error for a chosen task versus the total number of examples $n$ for all tasks. For GP covariances that are the product of an input-dependent covariance function and a free-form inter-task covariance matrix, we show that accurate approximations for the learning curve can be obtained for an arbitrary number of tasks $T$. We use these to study the asymptotic learning behaviour for large $n$. Surprisingly, multi-task learning can be asymptotically essentially useless, in the sense that examples from other tasks help only when the degree of inter-task correlation, $\rho$, is near its maximal value $\rho=1$. This effect is most extreme for learning of smooth target functions as described by e.g. squared exponential kernels. We also demonstrate that when learning many tasks, the learning curves separate into an initial phase, where the Bayes error on each task is reduced down to a plateau value by "collective learning" even though most tasks have not seen examples, and a final decay that occurs once the number of examples is proportional to the number of tasks.