Simon R. F. Ashton
Learning curves for multi-task Gaussian process regression
Nov 02, 2012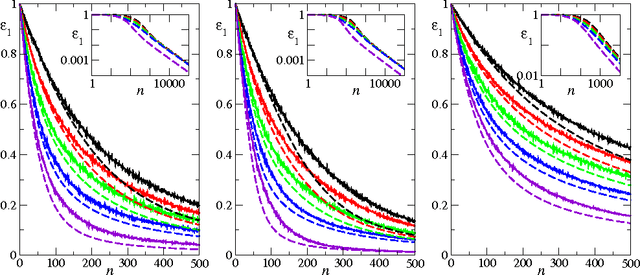
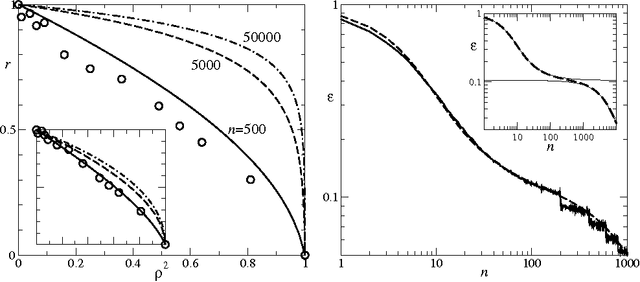
Abstract:We study the average case performance of multi-task Gaussian process (GP) regression as captured in the learning curve, i.e. the average Bayes error for a chosen task versus the total number of examples $n$ for all tasks. For GP covariances that are the product of an input-dependent covariance function and a free-form inter-task covariance matrix, we show that accurate approximations for the learning curve can be obtained for an arbitrary number of tasks $T$. We use these to study the asymptotic learning behaviour for large $n$. Surprisingly, multi-task learning can be asymptotically essentially useless, in the sense that examples from other tasks help only when the degree of inter-task correlation, $\rho$, is near its maximal value $\rho=1$. This effect is most extreme for learning of smooth target functions as described by e.g. squared exponential kernels. We also demonstrate that when learning many tasks, the learning curves separate into an initial phase, where the Bayes error on each task is reduced down to a plateau value by "collective learning" even though most tasks have not seen examples, and a final decay that occurs once the number of examples is proportional to the number of tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge