Pattern reconstruction with restricted Boltzmann machines

We show that the ability of a restricted Boltzmann machine to reconstruct a random pattern depends on the tail of the hidden prior distribution: hidden priors with strictly sub-Gaussian tails give only a logarithmic loss in pattern retrieval, while an efficient retrieval is much harder with hidden units with strictly super-Gaussian tails; reconstruction with sub-Gaussian hidden prior is regulated by the number of hidden units (as in the Hopfield model). This is proved by localisation estimates for the local minima of the energy function.

Minimax formula for the replica symmetric free energy of deep restricted Boltzmann machines

We study the free energy of a most used deep architecture for restricted Boltzmann machines, where the layers are disposed in series. Assuming independent Gaussian distributed random weights, we show that the error term in the so-called replica symmetric sum rule can be optimised as a saddle point. This leads us to conjecture that in the replica symmetric approximation the free energy is given by a min max formula, which parallels the one achieved for two-layer case.

Phase transitions in Restricted Boltzmann Machines with generic priors

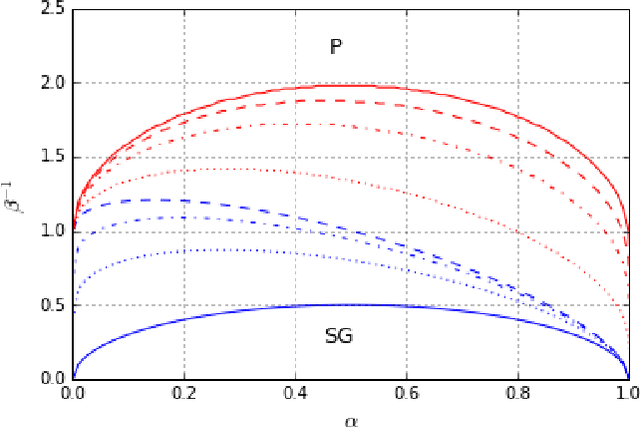
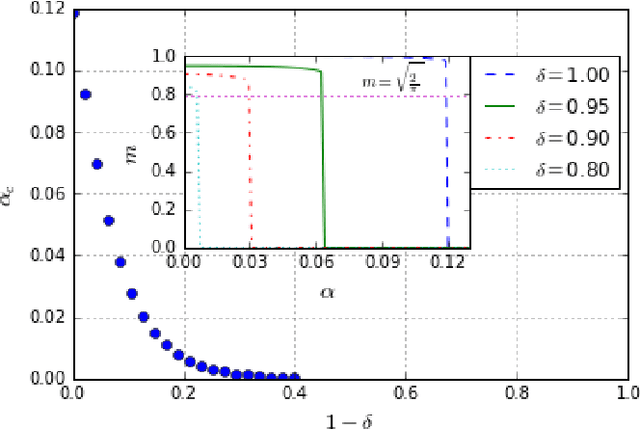
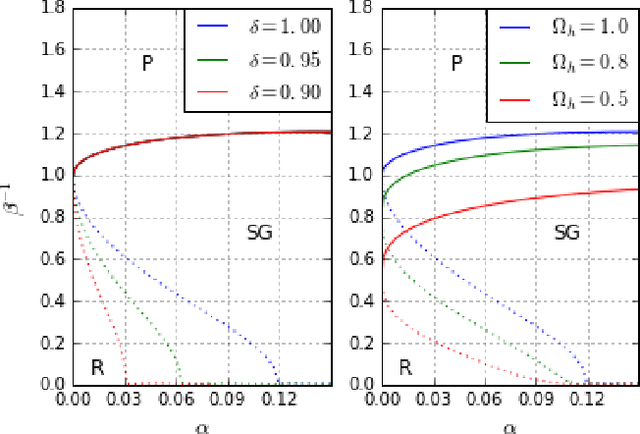
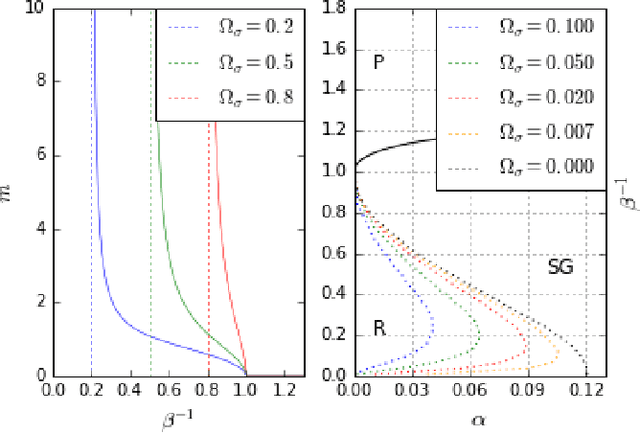
We study Generalised Restricted Boltzmann Machines with generic priors for units and weights, interpolating between Boolean and Gaussian variables. We present a complete analysis of the replica symmetric phase diagram of these systems, which can be regarded as Generalised Hopfield models. We underline the role of the retrieval phase for both inference and learning processes and we show that retrieval is robust for a large class of weight and unit priors, beyond the standard Hopfield scenario. Furthermore we show how the paramagnetic phase boundary is directly related to the optimal size of the training set necessary for good generalisation in a teacher-student scenario of unsupervised learning.

Phase Diagram of Restricted Boltzmann Machines and Generalised Hopfield Networks with Arbitrary Priors

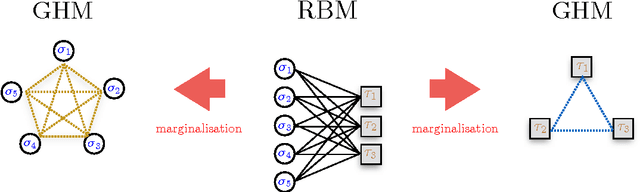
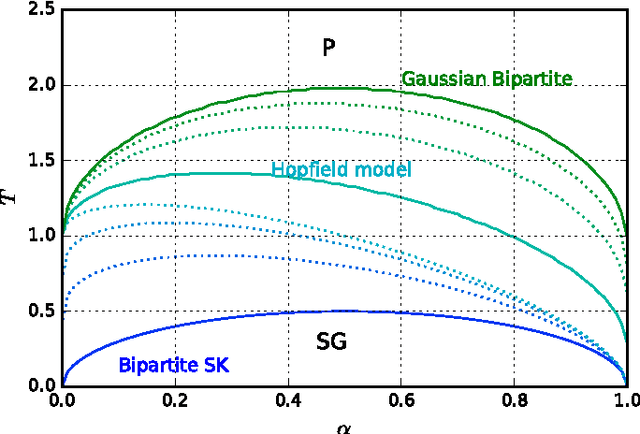
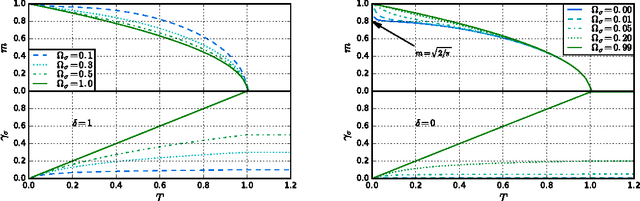
Restricted Boltzmann Machines are described by the Gibbs measure of a bipartite spin glass, which in turn corresponds to the one of a generalised Hopfield network. This equivalence allows us to characterise the state of these systems in terms of retrieval capabilities, both at low and high load. We study the paramagnetic-spin glass and the spin glass-retrieval phase transitions, as the pattern (i.e. weight) distribution and spin (i.e. unit) priors vary smoothly from Gaussian real variables to Boolean discrete variables. Our analysis shows that the presence of a retrieval phase is robust and not peculiar to the standard Hopfield model with Boolean patterns. The retrieval region is larger when the pattern entries and retrieval units get more peaked and, conversely, when the hidden units acquire a broader prior and therefore have a stronger response to high fields. Moreover, at low load retrieval always exists below some critical temperature, for every pattern distribution ranging from the Boolean to the Gaussian case.