The effect of priors on Learning with Restricted Boltzmann Machines

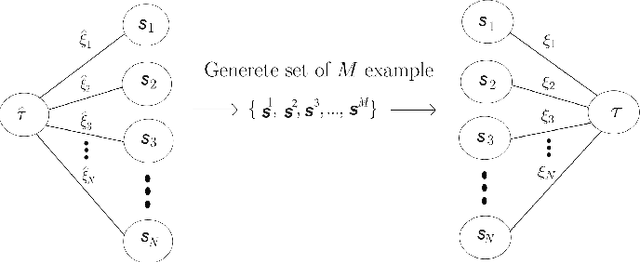
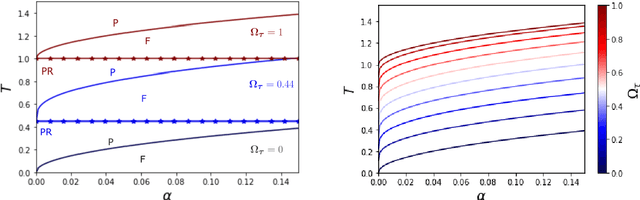
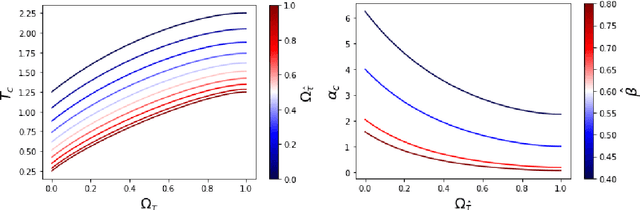
Restricted Boltzmann Machines (RBMs) are generative models designed to learn from data with a rich underlying structure. In this work, we explore a teacher-student setting where a student RBM learns from examples generated by a teacher RBM, with a focus on the effect of the unit priors on learning efficiency. We consider a parametric class of priors that interpolate between continuous (Gaussian) and binary variables. This approach models various possible choices of visible units, hidden units, and weights for both the teacher and student RBMs. By analyzing the phase diagram of the posterior distribution in both the Bayes optimal and mismatched regimes, we demonstrate the existence of a triple point that defines the critical dataset size necessary for learning through generalization. The critical size is strongly influenced by the properties of the teacher, and thus the data, but is unaffected by the properties of the student RBM. Nevertheless, a prudent choice of student priors can facilitate training by expanding the so-called signal retrieval region, where the machine generalizes effectively.

Modelling Structured Data Learning with Restricted Boltzmann Machines in the Teacher-Student Setting

Restricted Boltzmann machines (RBM) are generative models capable to learn data with a rich underlying structure. We study the teacher-student setting where a student RBM learns structured data generated by a teacher RBM. The amount of structure in the data is controlled by adjusting the number of hidden units of the teacher and the correlations in the rows of the weights, a.k.a. patterns. In the absence of correlations, we validate the conjecture that the performance is independent of the number of teacher patters and hidden units of the student RBMs, and we argue that the teacher-student setting can be used as a toy model for studying the lottery ticket hypothesis. Beyond this regime, we find that the critical amount of data required to learn the teacher patterns decreases with both their number and correlations. In both regimes, we find that, even with an relatively large dataset, it becomes impossible to learn the teacher patterns if the inference temperature used for regularization is kept too low. In our framework, the student can learn teacher patterns one-to-one or many-to-one, generalizing previous findings about the teacher-student setting with two hidden units to any arbitrary finite number of hidden units.

Dense Hopfield Networks in the Teacher-Student Setting

Dense Hopfield networks are known for their feature to prototype transition and adversarial robustness. However, previous theoretical studies have been mostly concerned with their storage capacity. We bridge this gap by studying the phase diagram of p-body Hopfield networks in the teacher-student setting of an unsupervised learning problem, uncovering ferromagnetic phases reminiscent of the prototype and feature learning regimes. On the Nishimori line, we find the critical size of the training set necessary for efficient pattern retrieval. Interestingly, we find that that the paramagnetic to ferromagnetic transition of the teacher-student setting coincides with the paramagnetic to spin-glass transition of the direct model, i.e. with random patterns. Outside of the Nishimori line, we investigate the learning performance in relation to the inference temperature and dataset noise. Moreover, we show that using a larger p for the student than the teacher gives the student an extensive tolerance to noise. We then derive a closed-form expression measuring the adversarial robustness of such a student at zero temperature, corroborating the positive correlation between number of parameters and robustness observed in large neural networks. We also use our model to clarify why the prototype phase of modern Hopfield networks is adversarially robust.

Hopfield model with planted patterns: a teacher-student self-supervised learning model

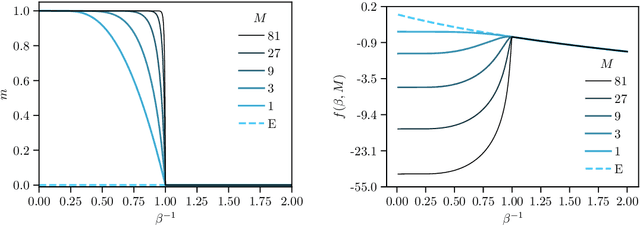
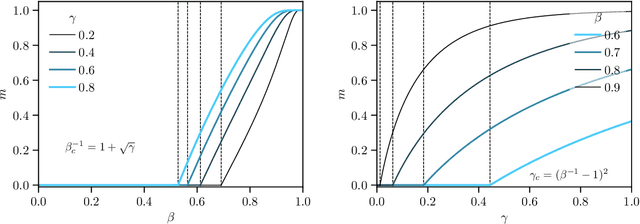
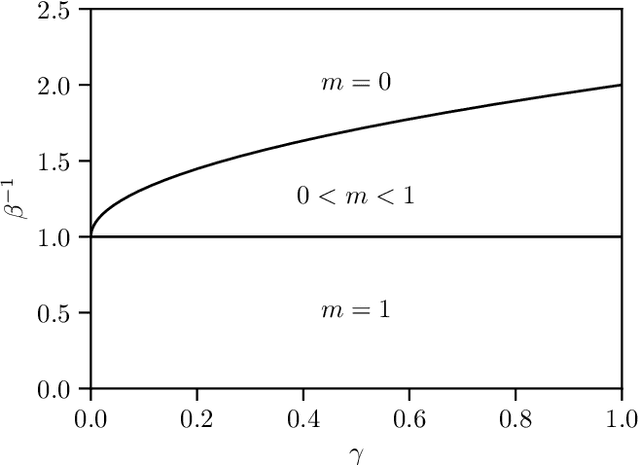
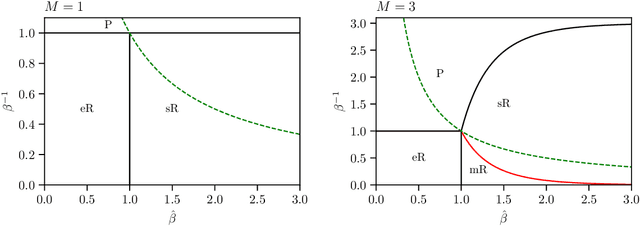
While Hopfield networks are known as paradigmatic models for memory storage and retrieval, modern artificial intelligence systems mainly stand on the machine learning paradigm. We show that it is possible to formulate a teacher-student self-supervised learning problem with Boltzmann machines in terms of a suitable generalization of the Hopfield model with structured patterns, where the spin variables are the machine weights and patterns correspond to the training set's examples. We analyze the learning performance by studying the phase diagram in terms of the training set size, the dataset noise and the inference temperature (i.e. the weight regularization). With a small but informative dataset the machine can learn by memorization. With a noisy dataset, an extensive number of examples above a critical threshold is needed. In this regime the memory storage limits of the system becomes an opportunity for the occurrence of a learning regime in which the system can generalize.

Reinforcement Learning Policy Recommendation for Interbank Network Stability

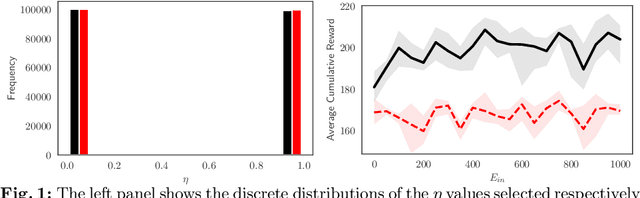
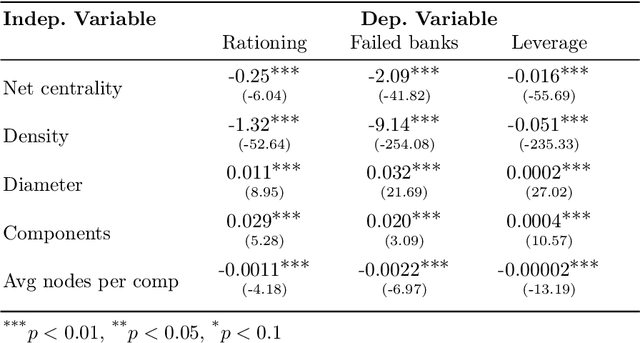
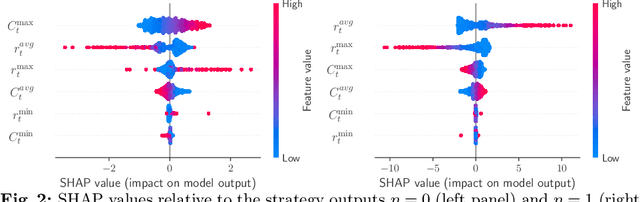
In this paper we analyze the effect of a policy recommendation on the performances of an artificial interbank market. Financial institutions stipulate lending agreements following a public recommendation and their individual information. The former, modeled by a reinforcement learning optimal policy trying to maximize the long term fitness of the system, gathers information on the economic environment and directs economic actors to create credit relationships based on the optimal choice between a low interest rate or high liquidity supply. The latter, based on the agents' balance sheet, allows to determine the liquidity supply and interest rate that the banks optimally offer on the market. Based on the combination between the public and the private signal, financial institutions create or cut their credit connections over time via a preferential attachment evolving procedure able to generate a dynamic network. Our results show that the emergence of a core-periphery interbank network, combined with a certain level of homogeneity on the size of lenders and borrowers, are essential features to ensure the resilience of the system. Moreover, the reinforcement learning optimal policy recommendation plays a crucial role in mitigating systemic risk with respect to alternative policy instruments.

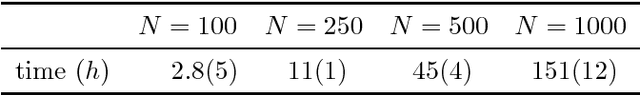
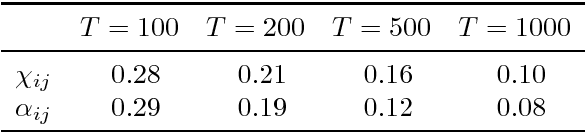
A dynamic network model with persistent links and node-specific latent variables, with an application to the interbank market

We propose a dynamic network model where two mechanisms control the probability of a link between two nodes: (i) the existence or absence of this link in the past, and (ii) node-specific latent variables (dynamic fitnesses) describing the propensity of each node to create links. Assuming a Markov dynamics for both mechanisms, we propose an Expectation-Maximization algorithm for model estimation and inference of the latent variables. The estimated parameters and fitnesses can be used to forecast the presence of a link in the future. We apply our methodology to the e-MID interbank network for which the two linkage mechanisms are associated with two different trading behaviors in the process of network formation, namely preferential trading and trading driven by node-specific characteristics. The empirical results allow to recognise preferential lending in the interbank market and indicate how a method that does not account for time-varying network topologies tends to overestimate preferential linkage.

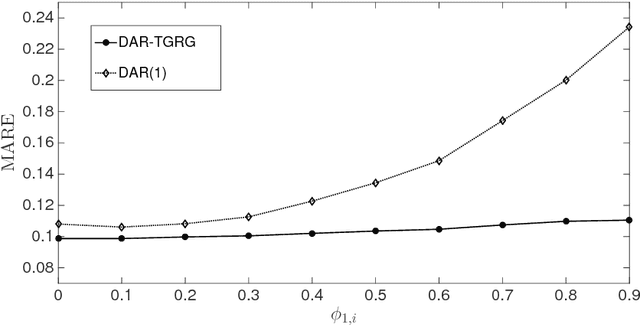
Disentangling group and link persistence in Dynamic Stochastic Block models

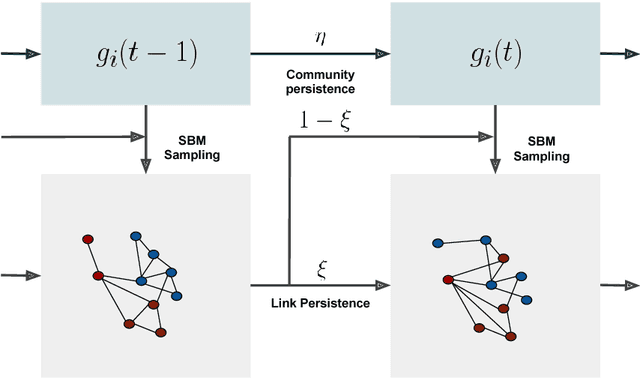
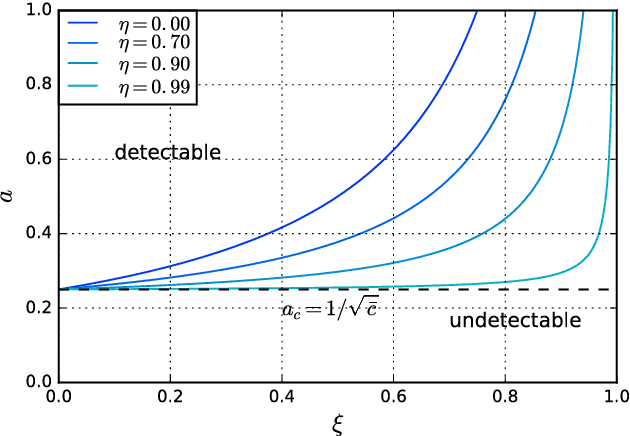
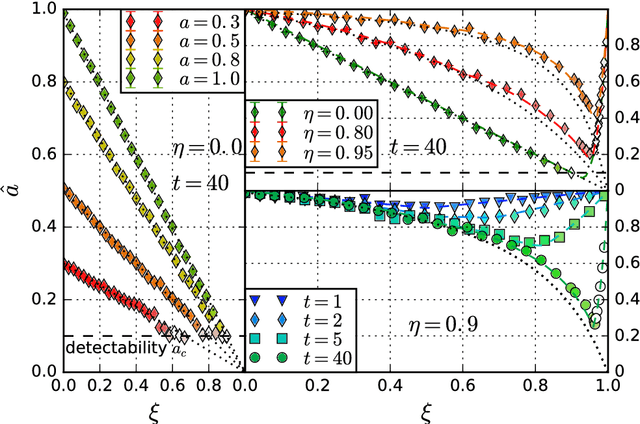
We study the inference of a model of dynamic networks in which both communities and links keep memory of previous network states. By considering maximum likelihood inference from single snapshot observations of the network, we show that link persistence makes the inference of communities harder, decreasing the detectability threshold, while community persistence tends to make it easier. We analytically show that communities inferred from single network snapshot can share a maximum overlap with the underlying communities of a specific previous instant in time. This leads to time-lagged inference: the identification of past communities rather than present ones. Finally we compute the time lag and propose a corrected algorithm, the Lagged Snapshot Dynamic (LSD) algorithm, for community detection in dynamic networks. We analytically and numerically characterize the detectability transitions of such algorithm as a function of the memory parameters of the model.

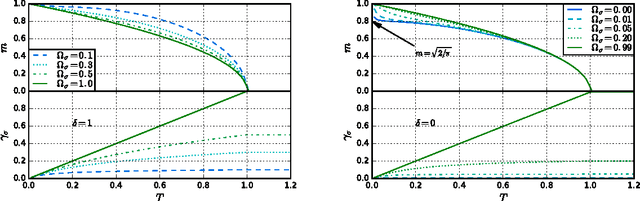
Phase transitions in Restricted Boltzmann Machines with generic priors

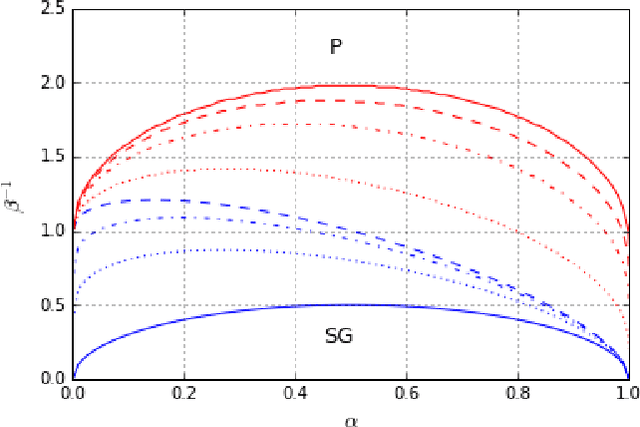
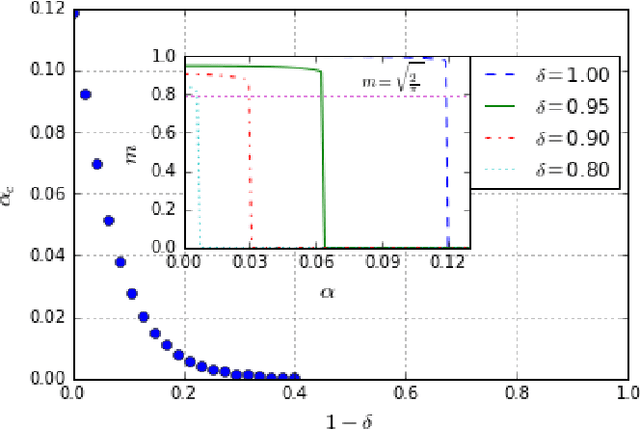
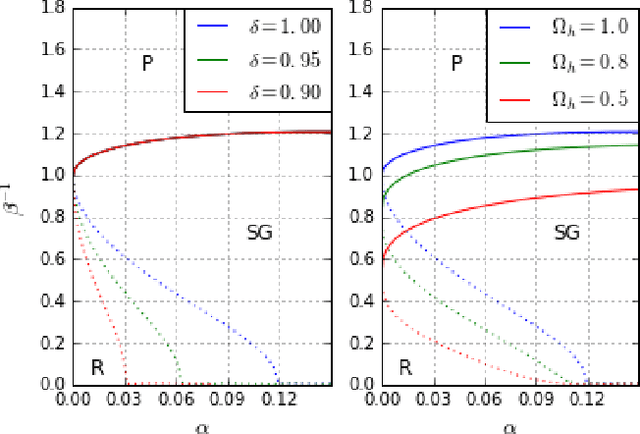
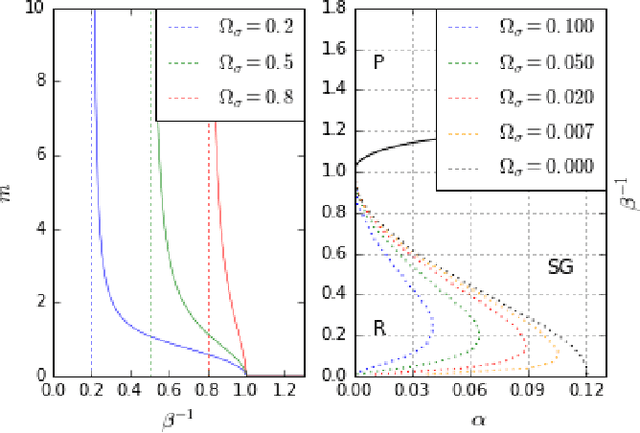
We study Generalised Restricted Boltzmann Machines with generic priors for units and weights, interpolating between Boolean and Gaussian variables. We present a complete analysis of the replica symmetric phase diagram of these systems, which can be regarded as Generalised Hopfield models. We underline the role of the retrieval phase for both inference and learning processes and we show that retrieval is robust for a large class of weight and unit priors, beyond the standard Hopfield scenario. Furthermore we show how the paramagnetic phase boundary is directly related to the optimal size of the training set necessary for good generalisation in a teacher-student scenario of unsupervised learning.

Phase Diagram of Restricted Boltzmann Machines and Generalised Hopfield Networks with Arbitrary Priors

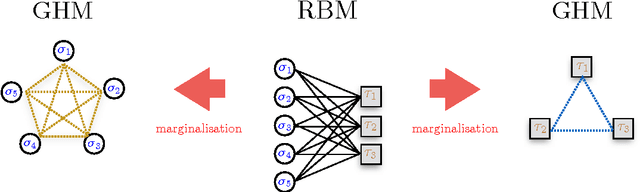
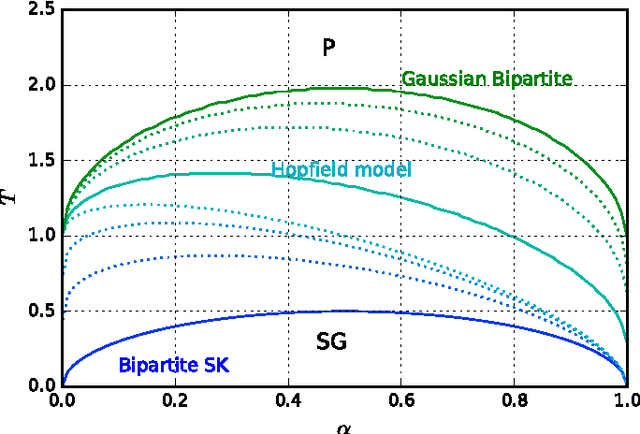
Restricted Boltzmann Machines are described by the Gibbs measure of a bipartite spin glass, which in turn corresponds to the one of a generalised Hopfield network. This equivalence allows us to characterise the state of these systems in terms of retrieval capabilities, both at low and high load. We study the paramagnetic-spin glass and the spin glass-retrieval phase transitions, as the pattern (i.e. weight) distribution and spin (i.e. unit) priors vary smoothly from Gaussian real variables to Boolean discrete variables. Our analysis shows that the presence of a retrieval phase is robust and not peculiar to the standard Hopfield model with Boolean patterns. The retrieval region is larger when the pattern entries and retrieval units get more peaked and, conversely, when the hidden units acquire a broader prior and therefore have a stronger response to high fields. Moreover, at low load retrieval always exists below some critical temperature, for every pattern distribution ranging from the Boolean to the Gaussian case.