Residual subspace evolution strategies for nonlinear inverse problems

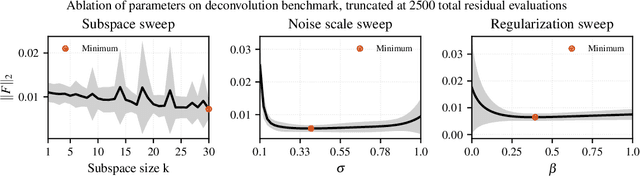
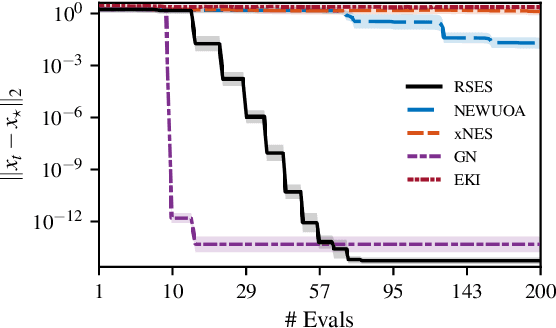
Nonlinear inverse problems pervade engineering and science, yet noisy, non-differentiable, or expensive residual evaluations routinely defeat Jacobian-based solvers. Derivative-free alternatives either demand smoothness, require large populations to stabilise covariance estimates, or stall on flat regions where gradient information fades. This paper introduces residual subspace evolution strategies (RSES), a derivative-free solver that draws Gaussian probes around the current iterate, records how residuals change along those directions, and recombines the probes through a least-squares solve to produce an optimal update. The method builds a residual-only surrogate without forming Jacobians or empirical covariances, and each iteration costs just $k+1$ residual evaluations with $O(k^3)$ linear algebra overhead, where $k$ remains far smaller than the parameter dimension. Benchmarks on calibration, regression, and deconvolution tasks show that RSES reduces misfit consistently across deterministic and stochastic settings, matching or exceeding xNES, NEWUOA, Adam, and ensemble Kalman inversion under matched evaluation budgets. The gains are most pronounced when smoothness or covariance assumptions break, suggesting that lightweight residual-difference surrogates can reliably guide descent where heavier machinery struggles.

Regularization, early-stopping and dreaming: a Hopfield-like setup to address generalization and overfitting

In this work we approach attractor neural networks from a machine learning perspective: we look for optimal network parameters by applying a gradient descent over a regularized loss function. Within this framework, the optimal neuron-interaction matrices turn out to be a class of matrices which correspond to Hebbian kernels revised by iteratively applying some unlearning protocols. Remarkably, the number of unlearning steps is proved to be related to the regularization hyperparameters of the loss function and to the training time. Thus, we can design strategies to avoid overfitting that are formulated in terms of the algebraic properties of the interaction matrix, or, equivalently, in terms of regularization tuning and early-stopping strategies. The generalization capabilities of these attractor networks are also investigated: analytical results are obtained for random synthetic datasets, next, the emerging picture is corroborated by numerical experiments that highlight the existence of several regimes (i.e., overfitting, failure and success) as the dataset parameters are varied.

Hopfield model with planted patterns: a teacher-student self-supervised learning model

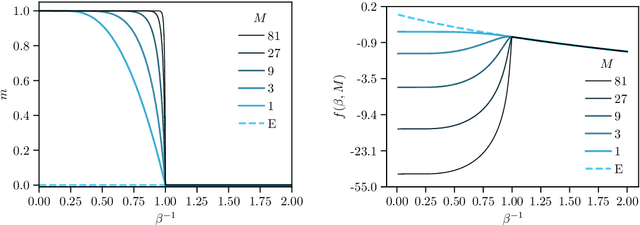
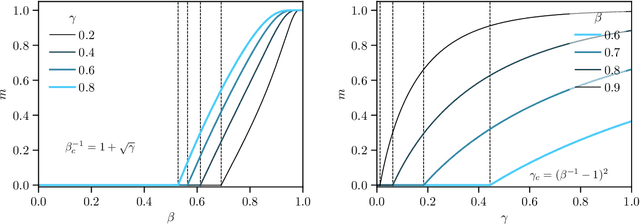
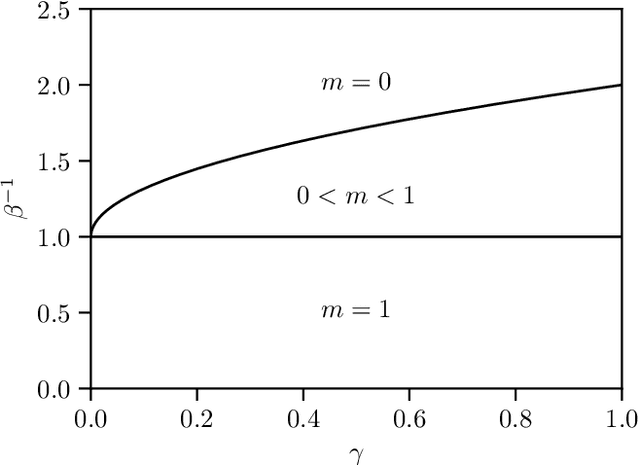
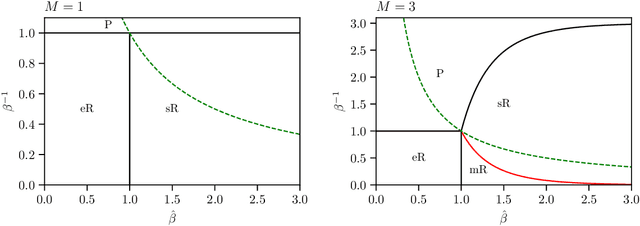
While Hopfield networks are known as paradigmatic models for memory storage and retrieval, modern artificial intelligence systems mainly stand on the machine learning paradigm. We show that it is possible to formulate a teacher-student self-supervised learning problem with Boltzmann machines in terms of a suitable generalization of the Hopfield model with structured patterns, where the spin variables are the machine weights and patterns correspond to the training set's examples. We analyze the learning performance by studying the phase diagram in terms of the training set size, the dataset noise and the inference temperature (i.e. the weight regularization). With a small but informative dataset the machine can learn by memorization. With a noisy dataset, an extensive number of examples above a critical threshold is needed. In this regime the memory storage limits of the system becomes an opportunity for the occurrence of a learning regime in which the system can generalize.

Dense Hebbian neural networks: a replica symmetric picture of supervised learning

We consider dense, associative neural-networks trained by a teacher (i.e., with supervision) and we investigate their computational capabilities analytically, via statistical-mechanics of spin glasses, and numerically, via Monte Carlo simulations. In particular, we obtain a phase diagram summarizing their performance as a function of the control parameters such as quality and quantity of the training dataset, network storage and noise, that is valid in the limit of large network size and structureless datasets: these networks may work in a ultra-storage regime (where they can handle a huge amount of patterns, if compared with shallow neural networks) or in a ultra-detection regime (where they can perform pattern recognition at prohibitive signal-to-noise ratios, if compared with shallow neural networks). Guided by the random theory as a reference framework, we also test numerically learning, storing and retrieval capabilities shown by these networks on structured datasets as MNist and Fashion MNist. As technical remarks, from the analytic side, we implement large deviations and stability analysis within Guerra's interpolation to tackle the not-Gaussian distributions involved in the post-synaptic potentials while, from the computational counterpart, we insert Plefka approximation in the Monte Carlo scheme, to speed up the evaluation of the synaptic tensors, overall obtaining a novel and broad approach to investigate supervised learning in neural networks, beyond the shallow limit, in general.

Dense Hebbian neural networks: a replica symmetric picture of unsupervised learning

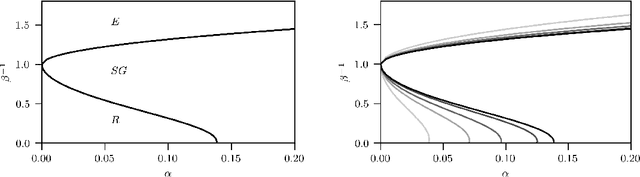
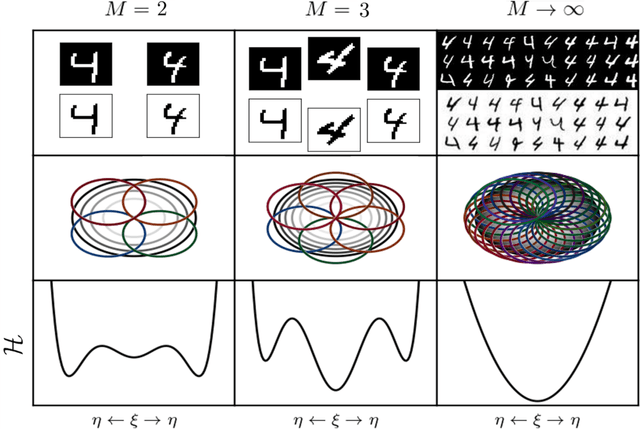
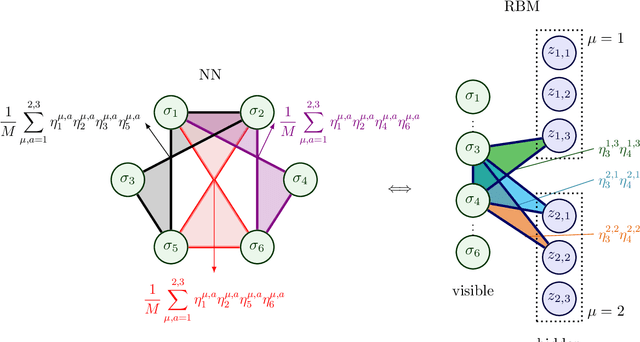
We consider dense, associative neural-networks trained with no supervision and we investigate their computational capabilities analytically, via a statistical-mechanics approach, and numerically, via Monte Carlo simulations. In particular, we obtain a phase diagram summarizing their performance as a function of the control parameters such as the quality and quantity of the training dataset and the network storage, valid in the limit of large network size and structureless datasets. Moreover, we establish a bridge between macroscopic observables standardly used in statistical mechanics and loss functions typically used in the machine learning. As technical remarks, from the analytic side, we implement large deviations and stability analysis within Guerra's interpolation to tackle the not-Gaussian distributions involved in the post-synaptic potentials while, from the computational counterpart, we insert Plefka approximation in the Monte Carlo scheme, to speed up the evaluation of the synaptic tensors, overall obtaining a novel and broad approach to investigate neural networks in general.

Recurrent neural networks that generalize from examples and optimize by dreaming

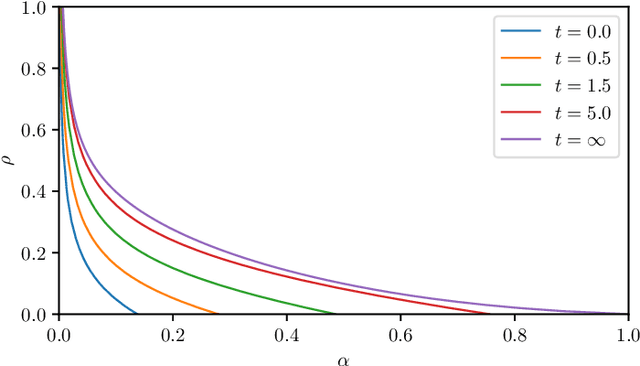
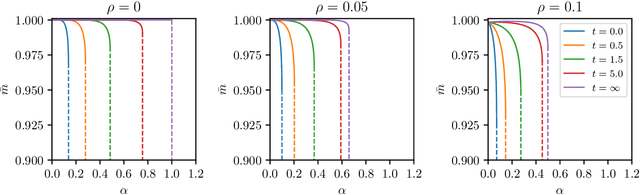
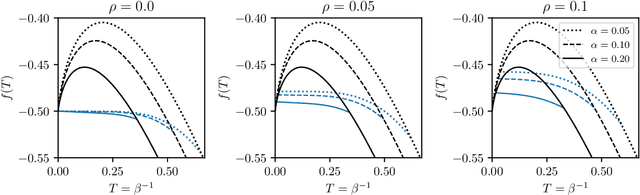
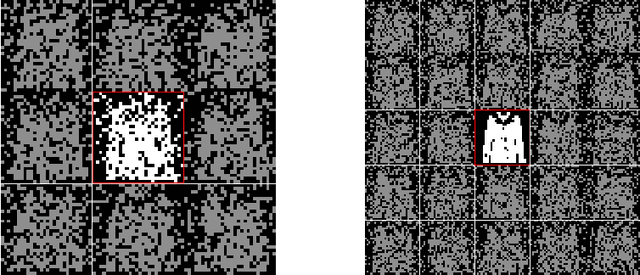
The gap between the huge volumes of data needed to train artificial neural networks and the relatively small amount of data needed by their biological counterparts is a central puzzle in machine learning. Here, inspired by biological information-processing, we introduce a generalized Hopfield network where pairwise couplings between neurons are built according to Hebb's prescription for on-line learning and allow also for (suitably stylized) off-line sleeping mechanisms. Moreover, in order to retain a learning framework, here the patterns are not assumed to be available, instead, we let the network experience solely a dataset made of a sample of noisy examples for each pattern. We analyze the model by statistical-mechanics tools and we obtain a quantitative picture of its capabilities as functions of its control parameters: the resulting network is an associative memory for pattern recognition that learns from examples on-line, generalizes and optimizes its storage capacity by off-line sleeping. Remarkably, the sleeping mechanisms always significantly reduce (up to $\approx 90\%$) the dataset size required to correctly generalize, further, there are memory loads that are prohibitive to Hebbian networks without sleeping (no matter the size and quality of the provided examples), but that are easily handled by the present "rested" neural networks.

Supervised Hebbian learning: toward eXplainable AI

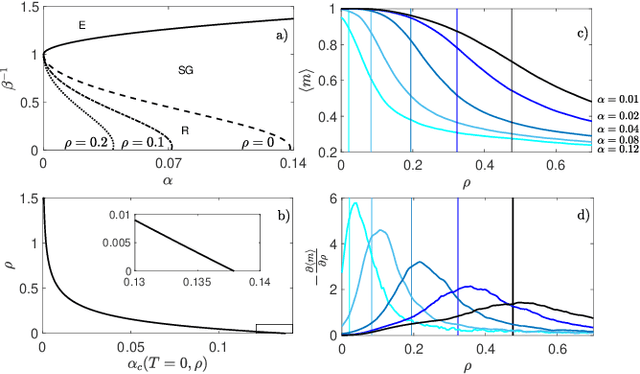
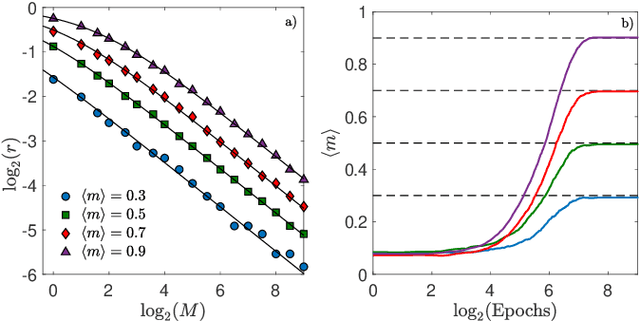
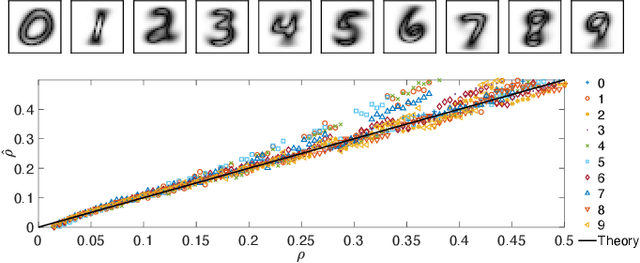
In neural network's Literature, {\em Hebbian learning} traditionally refers to the procedure by which the Hopfield model and its generalizations {\em store} archetypes (i.e., definite patterns that are experienced just once to form the synaptic matrix). However, the term {\em learning} in Machine Learning refers to the ability of the machine to extract features from the supplied dataset (e.g., made of blurred examples of these archetypes), in order to make its own representation of the unavailable archetypes. Here we prove that, if we feed the Hopfield model with blurred examples, we can define both {\em supervised} and {\em unsupervised} learning protocols by which the network can possibly infer the archetypes and we detect the correct control parameters (including the dataset size and its quality) to depict a phase diagram for the system performance. We also prove that, for random, structureless datasets, the Hopfield model equipped with a supervised learning rule is equivalent to a restricted Boltzmann machine and this suggests an optimal training routine; the robustness of results is also checked numerically for structured datasets. This work contributes to pave a solid way toward eXplainable AI (XAI).

The emergence of a concept in shallow neural networks

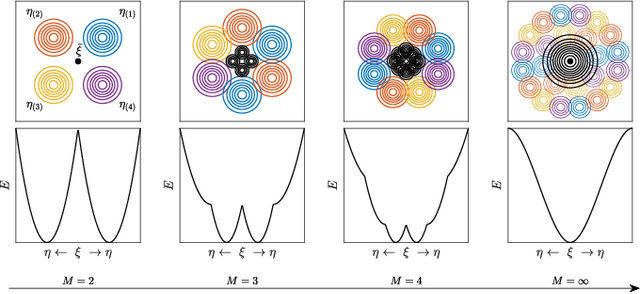
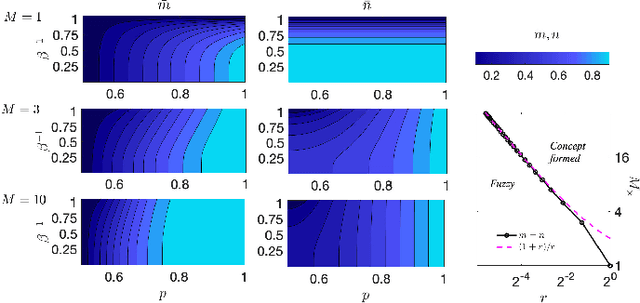
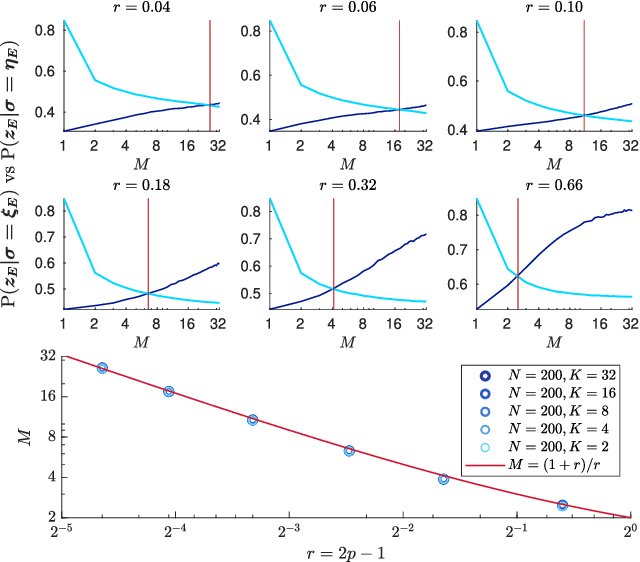
We consider restricted Boltzmann machine (RBMs) trained over an unstructured dataset made of blurred copies of definite but unavailable ``archetypes'' and we show that there exists a critical sample size beyond which the RBM can learn archetypes, namely the machine can successfully play as a generative model or as a classifier, according to the operational routine. In general, assessing a critical sample size (possibly in relation to the quality of the dataset) is still an open problem in machine learning. Here, restricting to the random theory, where shallow networks suffice and the grand-mother cell scenario is correct, we leverage the formal equivalence between RBMs and Hopfield networks, to obtain a phase diagram for both the neural architectures which highlights regions, in the space of the control parameters (i.e., number of archetypes, number of neurons, size and quality of the training set), where learning can be accomplished. Our investigations are led by analytical methods based on the statistical-mechanics of disordered systems and results are further corroborated by extensive Monte Carlo simulations.

Interpolating between boolean and extremely high noisy patterns through Minimal Dense Associative Memories

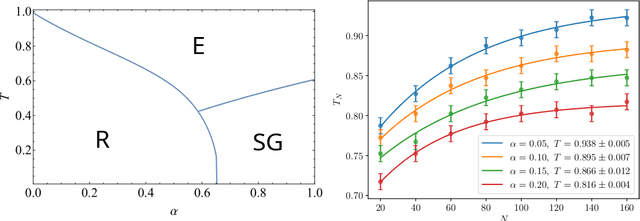
Recently, Hopfield and Krotov introduced the concept of {\em dense associative memories} [DAM] (close to spin-glasses with $P$-wise interactions in a disordered statistical mechanical jargon): they proved a number of remarkable features these networks share and suggested their use to (partially) explain the success of the new generation of Artificial Intelligence. Thanks to a remarkable ante-litteram analysis by Baldi \& Venkatesh, among these properties, it is known these networks can handle a maximal amount of stored patterns $K$ scaling as $K \sim N^{P-1}$.\\ In this paper, once introduced a {\em minimal dense associative network} as one of the most elementary cost-functions falling in this class of DAM, we sacrifice this high-load regime -namely we force the storage of {\em solely} a linear amount of patterns, i.e. $K = \alpha N$ (with $\alpha>0$)- to prove that, in this regime, these networks can correctly perform pattern recognition even if pattern signal is $O(1)$ and is embedded in a sea of noise $O(\sqrt{N})$, also in the large $N$ limit. To prove this statement, by extremizing the quenched free-energy of the model over its natural order-parameters (the various magnetizations and overlaps), we derived its phase diagram, at the replica symmetric level of description and in the thermodynamic limit: as a sideline, we stress that, to achieve this task, aiming at cross-fertilization among disciplines, we pave two hegemon routes in the statistical mechanics of spin glasses, namely the replica trick and the interpolation technique.\\ Both the approaches reach the same conclusion: there is a not-empty region, in the noise-$T$ vs load-$\alpha$ phase diagram plane, where these networks can actually work in this challenging regime; in particular we obtained a quite high critical (linear) load in the (fast) noiseless case resulting in $\lim_{\beta \to \infty}\alpha_c(\beta)=0.65$.

Neural networks with redundant representation: detecting the undetectable

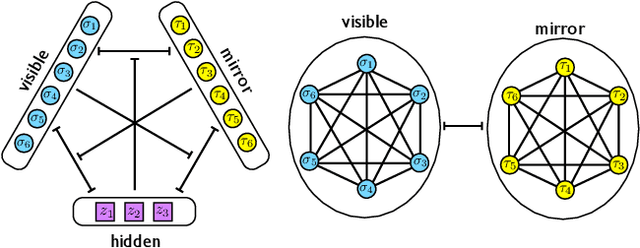
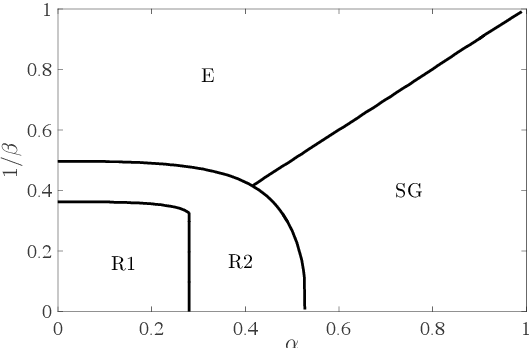
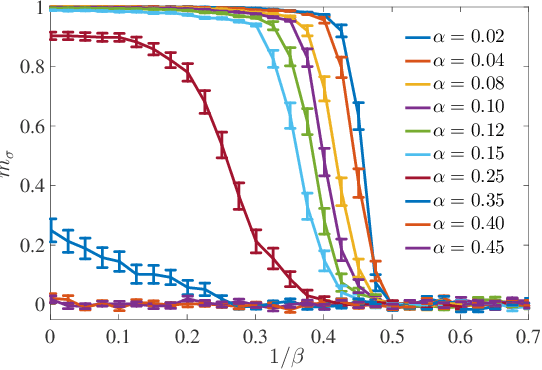
We consider a three-layer Sejnowski machine and show that features learnt via contrastive divergence have a dual representation as patterns in a dense associative memory of order P=4. The latter is known to be able to Hebbian-store an amount of patterns scaling as N^{P-1}, where N denotes the number of constituting binary neurons interacting P-wisely. We also prove that, by keeping the dense associative network far from the saturation regime (namely, allowing for a number of patterns scaling only linearly with N, while P>2) such a system is able to perform pattern recognition far below the standard signal-to-noise threshold. In particular, a network with P=4 is able to retrieve information whose intensity is O(1) even in the presence of a noise O(\sqrt{N}) in the large N limit. This striking skill stems from a redundancy representation of patterns -- which is afforded given the (relatively) low-load information storage -- and it contributes to explain the impressive abilities in pattern recognition exhibited by new-generation neural networks. The whole theory is developed rigorously, at the replica symmetric level of approximation, and corroborated by signal-to-noise analysis and Monte Carlo simulations.