Fundamental operating regimes, hyper-parameter fine-tuning and glassiness: towards an interpretable replica-theory for trained restricted Boltzmann machines

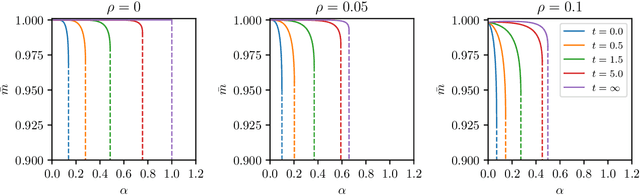
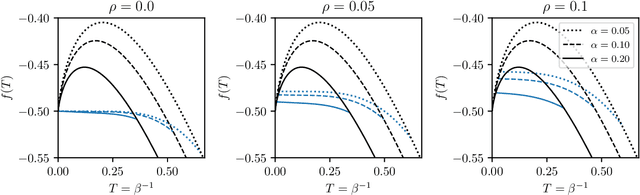
We consider restricted Boltzmann machines with a binary visible layer and a Gaussian hidden layer trained by an unlabelled dataset composed of noisy realizations of a single ground pattern. We develop a statistical mechanics framework to describe the network generative capabilities, by exploiting the replica trick and assuming self-averaging of the underlying order parameters (i.e., replica symmetry). In particular, we outline the effective control parameters (e.g., the relative number of weights to be trained, the regularization parameter), whose tuning can yield qualitatively-different operative regimes. Further, we provide analytical and numerical evidence for the existence of a sub-region in the space of the hyperparameters where replica-symmetry breaking occurs.

Regularization, early-stopping and dreaming: a Hopfield-like setup to address generalization and overfitting

In this work we approach attractor neural networks from a machine learning perspective: we look for optimal network parameters by applying a gradient descent over a regularized loss function. Within this framework, the optimal neuron-interaction matrices turn out to be a class of matrices which correspond to Hebbian kernels revised by iteratively applying some unlearning protocols. Remarkably, the number of unlearning steps is proved to be related to the regularization hyperparameters of the loss function and to the training time. Thus, we can design strategies to avoid overfitting that are formulated in terms of the algebraic properties of the interaction matrix, or, equivalently, in terms of regularization tuning and early-stopping strategies. The generalization capabilities of these attractor networks are also investigated: analytical results are obtained for random synthetic datasets, next, the emerging picture is corroborated by numerical experiments that highlight the existence of several regimes (i.e., overfitting, failure and success) as the dataset parameters are varied.

Pavlov Learning Machines

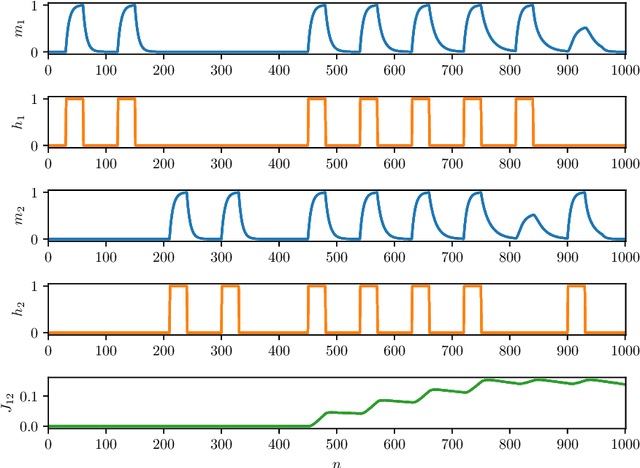
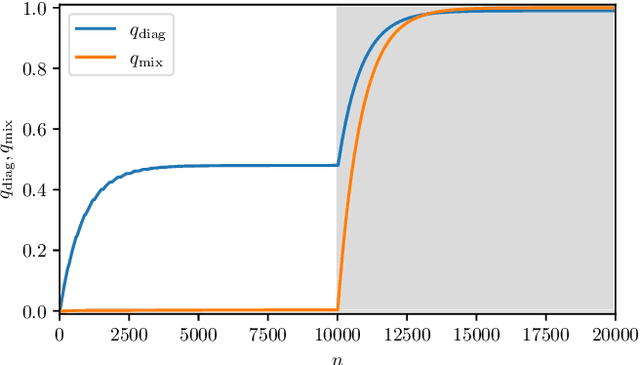
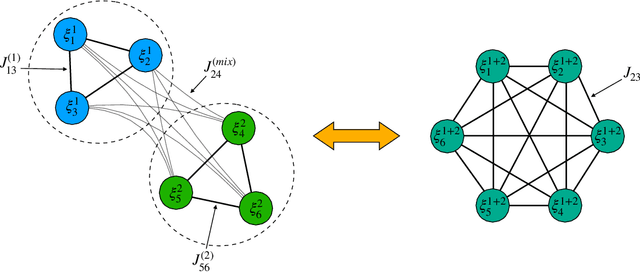
As well known, Hebb's learning traces its origin in Pavlov's Classical Conditioning, however, while the former has been extensively modelled in the past decades (e.g., by Hopfield model and countless variations on theme), as for the latter modelling has remained largely unaddressed so far; further, a bridge between these two pillars is totally lacking. The main difficulty towards this goal lays in the intrinsically different scales of the information involved: Pavlov's theory is about correlations among \emph{concepts} that are (dynamically) stored in the synaptic matrix as exemplified by the celebrated experiment starring a dog and a ring bell; conversely, Hebb's theory is about correlations among pairs of adjacent neurons as summarized by the famous statement {\em neurons that fire together wire together}. In this paper we rely on stochastic-process theory and model neural and synaptic dynamics via Langevin equations, to prove that -- as long as we keep neurons' and synapses' timescales largely split -- Pavlov mechanism spontaneously takes place and ultimately gives rise to synaptic weights that recover the Hebbian kernel.

Recurrent neural networks that generalize from examples and optimize by dreaming

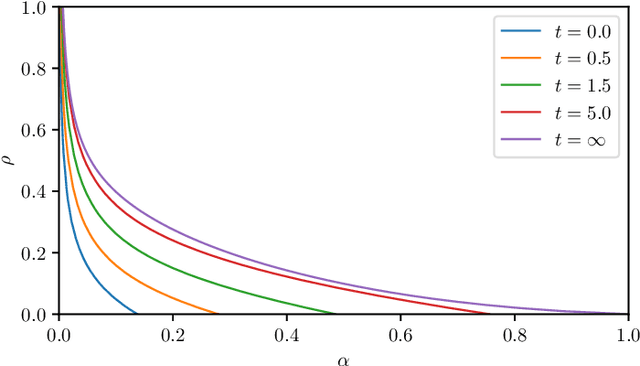
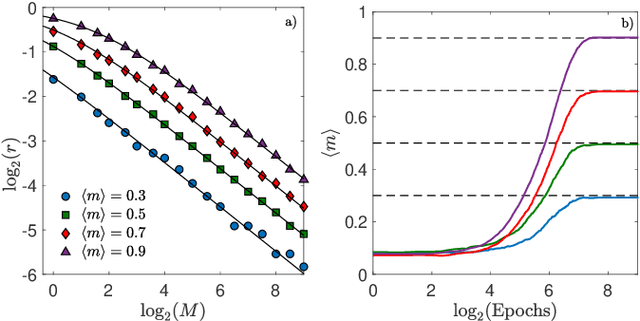
The gap between the huge volumes of data needed to train artificial neural networks and the relatively small amount of data needed by their biological counterparts is a central puzzle in machine learning. Here, inspired by biological information-processing, we introduce a generalized Hopfield network where pairwise couplings between neurons are built according to Hebb's prescription for on-line learning and allow also for (suitably stylized) off-line sleeping mechanisms. Moreover, in order to retain a learning framework, here the patterns are not assumed to be available, instead, we let the network experience solely a dataset made of a sample of noisy examples for each pattern. We analyze the model by statistical-mechanics tools and we obtain a quantitative picture of its capabilities as functions of its control parameters: the resulting network is an associative memory for pattern recognition that learns from examples on-line, generalizes and optimizes its storage capacity by off-line sleeping. Remarkably, the sleeping mechanisms always significantly reduce (up to $\approx 90\%$) the dataset size required to correctly generalize, further, there are memory loads that are prohibitive to Hebbian networks without sleeping (no matter the size and quality of the provided examples), but that are easily handled by the present "rested" neural networks.

Supervised Hebbian learning: toward eXplainable AI

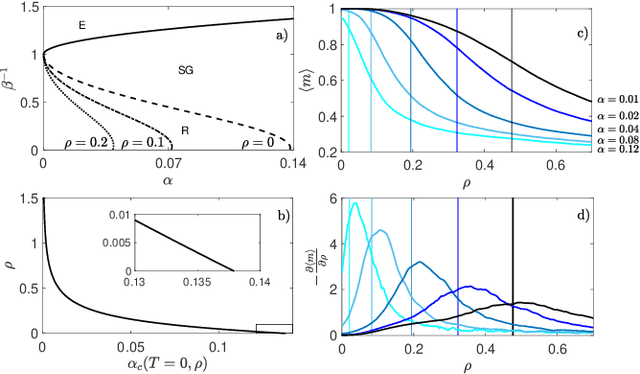
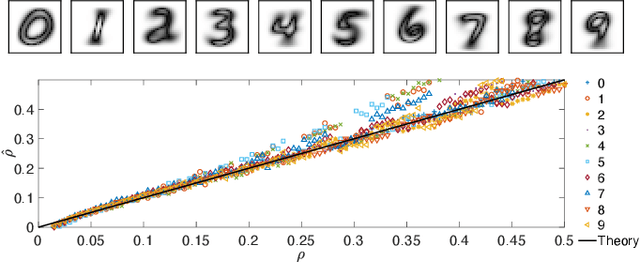
In neural network's Literature, {\em Hebbian learning} traditionally refers to the procedure by which the Hopfield model and its generalizations {\em store} archetypes (i.e., definite patterns that are experienced just once to form the synaptic matrix). However, the term {\em learning} in Machine Learning refers to the ability of the machine to extract features from the supplied dataset (e.g., made of blurred examples of these archetypes), in order to make its own representation of the unavailable archetypes. Here we prove that, if we feed the Hopfield model with blurred examples, we can define both {\em supervised} and {\em unsupervised} learning protocols by which the network can possibly infer the archetypes and we detect the correct control parameters (including the dataset size and its quality) to depict a phase diagram for the system performance. We also prove that, for random, structureless datasets, the Hopfield model equipped with a supervised learning rule is equivalent to a restricted Boltzmann machine and this suggests an optimal training routine; the robustness of results is also checked numerically for structured datasets. This work contributes to pave a solid way toward eXplainable AI (XAI).