CAP: Detecting Unauthorized Data Usage in Generative Models via Prompt Generation

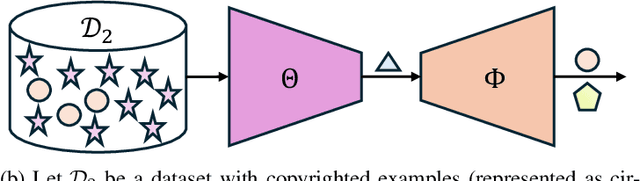
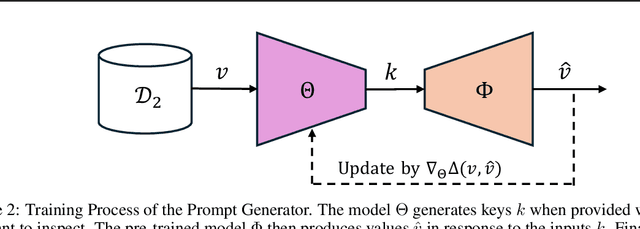
To achieve accurate and unbiased predictions, Machine Learning (ML) models rely on large, heterogeneous, and high-quality datasets. However, this could raise ethical and legal concerns regarding copyright and authorization aspects, especially when information is gathered from the Internet. With the rise of generative models, being able to track data has become of particular importance, especially since they may (un)intentionally replicate copyrighted contents. Therefore, this work proposes Copyright Audit via Prompts generation (CAP), a framework for automatically testing whether an ML model has been trained with unauthorized data. Specifically, we devise an approach to generate suitable keys inducing the model to reveal copyrighted contents. To prove its effectiveness, we conducted an extensive evaluation campaign on measurements collected in four IoT scenarios. The obtained results showcase the effectiveness of CAP, when used against both realistic and synthetic datasets.

Hebbian Learning from First Principles

Recently, the original storage prescription for the Hopfield model of neural networks -- as well as for its dense generalizations -- has been turned into a genuine Hebbian learning rule by postulating the expression of its Hamiltonian for both the supervised and unsupervised protocols. In these notes, first, we obtain these explicit expressions by relying upon maximum entropy extremization \`a la Jaynes. Beyond providing a formal derivation of these recipes for Hebbian learning, this construction also highlights how Lagrangian constraints within entropy extremization force network's outcomes on neural correlations: these try to mimic the empirical counterparts hidden in the datasets provided to the network for its training and, the denser the network, the longer the correlations that it is able to capture. Next, we prove that, in the big data limit, whatever the presence of a teacher (or its lacking), not only these Hebbian learning rules converge to the original storage prescription of the Hopfield model but also their related free energies (and, thus, the statistical mechanical picture provided by Amit, Gutfreund and Sompolinsky is fully recovered). As a sideline, we show mathematical equivalence among standard Cost functions (Hamiltonian), preferred in Statistical Mechanical jargon, and quadratic Loss Functions, preferred in Machine Learning terminology. Remarks on the exponential Hopfield model (as the limit of dense networks with diverging density) and semi-supervised protocols are also provided.

Recurrent neural networks that generalize from examples and optimize by dreaming

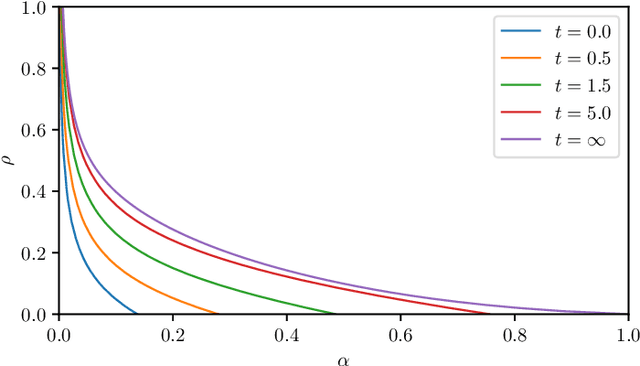
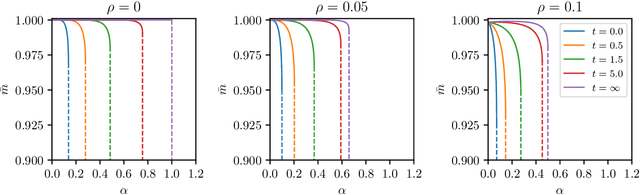
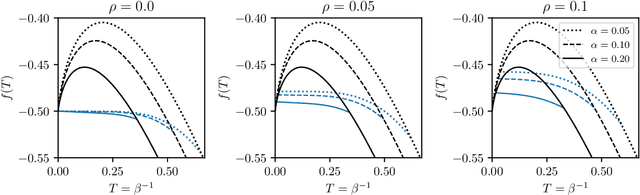
The gap between the huge volumes of data needed to train artificial neural networks and the relatively small amount of data needed by their biological counterparts is a central puzzle in machine learning. Here, inspired by biological information-processing, we introduce a generalized Hopfield network where pairwise couplings between neurons are built according to Hebb's prescription for on-line learning and allow also for (suitably stylized) off-line sleeping mechanisms. Moreover, in order to retain a learning framework, here the patterns are not assumed to be available, instead, we let the network experience solely a dataset made of a sample of noisy examples for each pattern. We analyze the model by statistical-mechanics tools and we obtain a quantitative picture of its capabilities as functions of its control parameters: the resulting network is an associative memory for pattern recognition that learns from examples on-line, generalizes and optimizes its storage capacity by off-line sleeping. Remarkably, the sleeping mechanisms always significantly reduce (up to $\approx 90\%$) the dataset size required to correctly generalize, further, there are memory loads that are prohibitive to Hebbian networks without sleeping (no matter the size and quality of the provided examples), but that are easily handled by the present "rested" neural networks.