The effect of priors on Learning with Restricted Boltzmann Machines

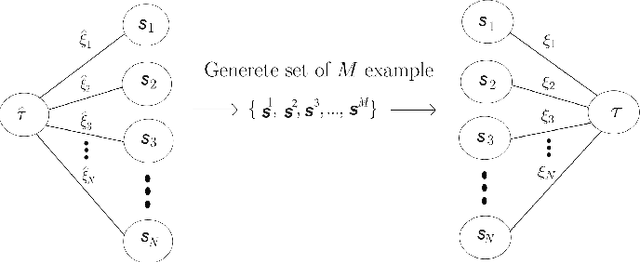
Restricted Boltzmann Machines (RBMs) are generative models designed to learn from data with a rich underlying structure. In this work, we explore a teacher-student setting where a student RBM learns from examples generated by a teacher RBM, with a focus on the effect of the unit priors on learning efficiency. We consider a parametric class of priors that interpolate between continuous (Gaussian) and binary variables. This approach models various possible choices of visible units, hidden units, and weights for both the teacher and student RBMs. By analyzing the phase diagram of the posterior distribution in both the Bayes optimal and mismatched regimes, we demonstrate the existence of a triple point that defines the critical dataset size necessary for learning through generalization. The critical size is strongly influenced by the properties of the teacher, and thus the data, but is unaffected by the properties of the student RBM. Nevertheless, a prudent choice of student priors can facilitate training by expanding the so-called signal retrieval region, where the machine generalizes effectively.

Hopfield model with planted patterns: a teacher-student self-supervised learning model

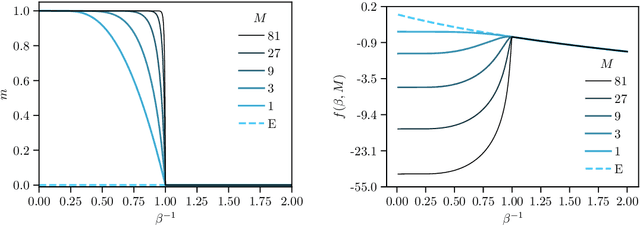
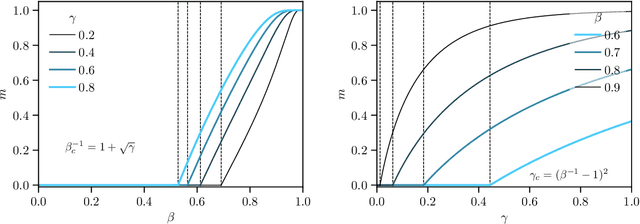
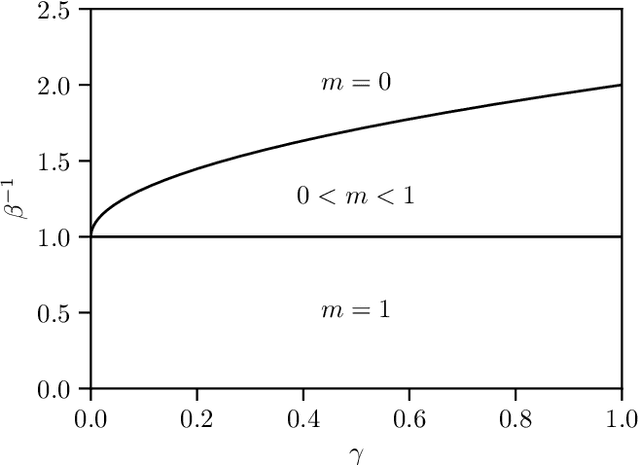
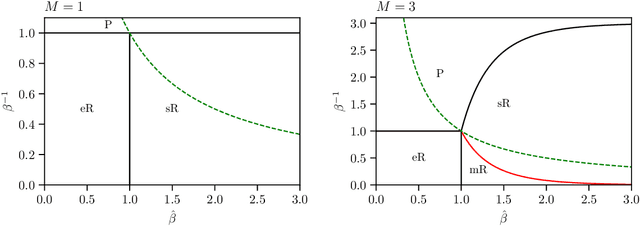
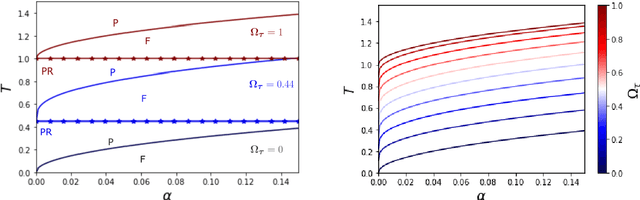
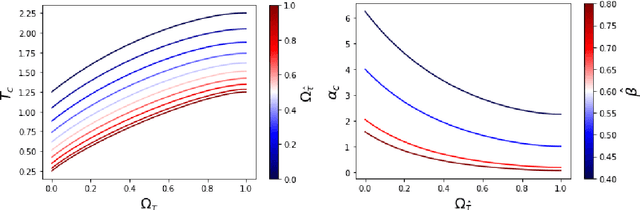
While Hopfield networks are known as paradigmatic models for memory storage and retrieval, modern artificial intelligence systems mainly stand on the machine learning paradigm. We show that it is possible to formulate a teacher-student self-supervised learning problem with Boltzmann machines in terms of a suitable generalization of the Hopfield model with structured patterns, where the spin variables are the machine weights and patterns correspond to the training set's examples. We analyze the learning performance by studying the phase diagram in terms of the training set size, the dataset noise and the inference temperature (i.e. the weight regularization). With a small but informative dataset the machine can learn by memorization. With a noisy dataset, an extensive number of examples above a critical threshold is needed. In this regime the memory storage limits of the system becomes an opportunity for the occurrence of a learning regime in which the system can generalize.