Interpolating between boolean and extremely high noisy patterns through Minimal Dense Associative Memories

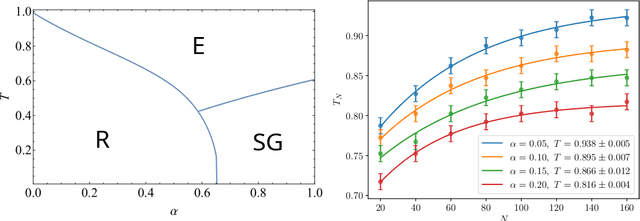
Recently, Hopfield and Krotov introduced the concept of {\em dense associative memories} [DAM] (close to spin-glasses with $P$-wise interactions in a disordered statistical mechanical jargon): they proved a number of remarkable features these networks share and suggested their use to (partially) explain the success of the new generation of Artificial Intelligence. Thanks to a remarkable ante-litteram analysis by Baldi \& Venkatesh, among these properties, it is known these networks can handle a maximal amount of stored patterns $K$ scaling as $K \sim N^{P-1}$.\\ In this paper, once introduced a {\em minimal dense associative network} as one of the most elementary cost-functions falling in this class of DAM, we sacrifice this high-load regime -namely we force the storage of {\em solely} a linear amount of patterns, i.e. $K = \alpha N$ (with $\alpha>0$)- to prove that, in this regime, these networks can correctly perform pattern recognition even if pattern signal is $O(1)$ and is embedded in a sea of noise $O(\sqrt{N})$, also in the large $N$ limit. To prove this statement, by extremizing the quenched free-energy of the model over its natural order-parameters (the various magnetizations and overlaps), we derived its phase diagram, at the replica symmetric level of description and in the thermodynamic limit: as a sideline, we stress that, to achieve this task, aiming at cross-fertilization among disciplines, we pave two hegemon routes in the statistical mechanics of spin glasses, namely the replica trick and the interpolation technique.\\ Both the approaches reach the same conclusion: there is a not-empty region, in the noise-$T$ vs load-$\alpha$ phase diagram plane, where these networks can actually work in this challenging regime; in particular we obtained a quite high critical (linear) load in the (fast) noiseless case resulting in $\lim_{\beta \to \infty}\alpha_c(\beta)=0.65$.

Neural networks with redundant representation: detecting the undetectable

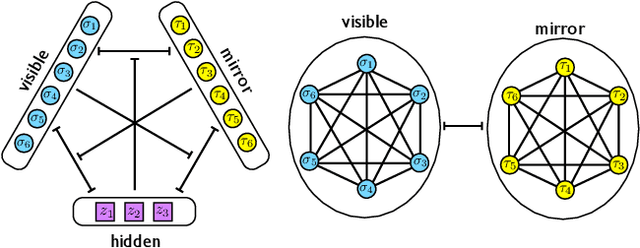
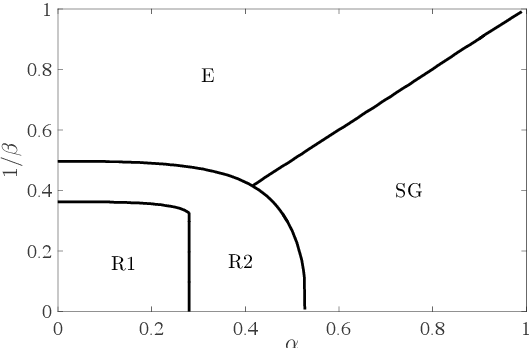
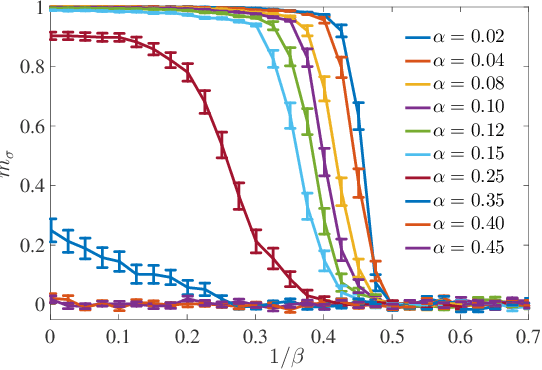
We consider a three-layer Sejnowski machine and show that features learnt via contrastive divergence have a dual representation as patterns in a dense associative memory of order P=4. The latter is known to be able to Hebbian-store an amount of patterns scaling as N^{P-1}, where N denotes the number of constituting binary neurons interacting P-wisely. We also prove that, by keeping the dense associative network far from the saturation regime (namely, allowing for a number of patterns scaling only linearly with N, while P>2) such a system is able to perform pattern recognition far below the standard signal-to-noise threshold. In particular, a network with P=4 is able to retrieve information whose intensity is O(1) even in the presence of a noise O(\sqrt{N}) in the large N limit. This striking skill stems from a redundancy representation of patterns -- which is afforded given the (relatively) low-load information storage -- and it contributes to explain the impressive abilities in pattern recognition exhibited by new-generation neural networks. The whole theory is developed rigorously, at the replica symmetric level of approximation, and corroborated by signal-to-noise analysis and Monte Carlo simulations.