Dynamical selection of Nash equilibria using Experience Weighted Attraction Learning: emergence of heterogeneous mixed equilibria
Paper and Code
Jun 29, 2017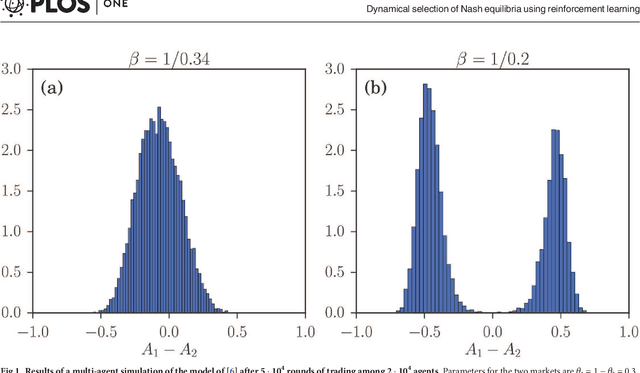
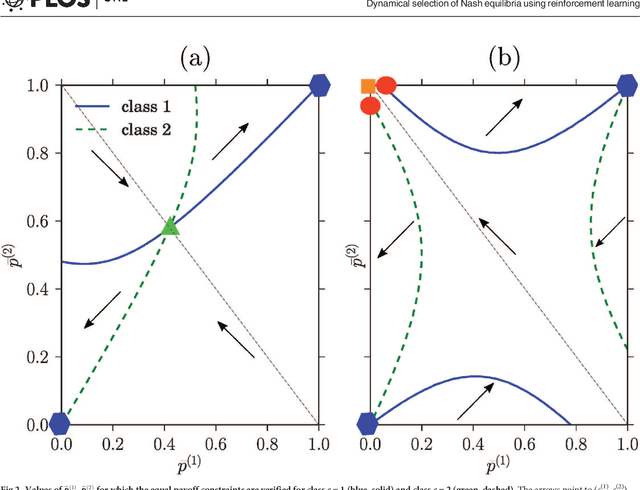
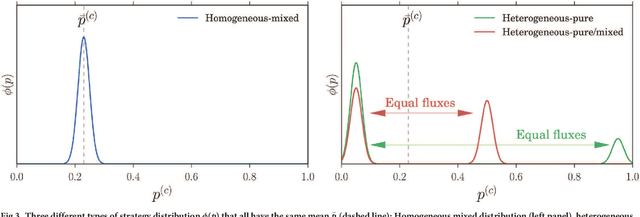

We study the distribution of strategies in a large game that models how agents choose among different double auction markets. We classify the possible mean field Nash equilibria, which include potentially segregated states where an agent population can split into subpopulations adopting different strategies. As the game is aggregative, the actual equilibrium strategy distributions remain undetermined, however. We therefore compare with the results of Experience-Weighted Attraction (EWA) learning, which at long times leads to Nash equilibria in the appropriate limits of large intensity of choice, low noise (long agent memory) and perfect imputation of missing scores (fictitious play). The learning dynamics breaks the indeterminacy of the Nash equilibria. Non-trivially, depending on how the relevant limits are taken, more than one type of equilibrium can be selected. These include the standard homogeneous mixed and heterogeneous pure states, but also \emph{heterogeneous mixed} states where different agents play different strategies that are not all pure. The analysis of the EWA learning involves Fokker-Planck modeling combined with large deviation methods. The theoretical results are confirmed by multi-agent simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge