GNN Explanations that do not Explain and How to find Them

Explanations provided by Self-explainable Graph Neural Networks (SE-GNNs) are fundamental for understanding the model's inner workings and for identifying potential misuse of sensitive attributes. Although recent works have highlighted that these explanations can be suboptimal and potentially misleading, a characterization of their failure cases is unavailable. In this work, we identify a critical failure of SE-GNN explanations: explanations can be unambiguously unrelated to how the SE-GNNs infer labels. We show that, on the one hand, many SE-GNNs can achieve optimal true risk while producing these degenerate explanations, and on the other, most faithfulness metrics can fail to identify these failure modes. Our empirical analysis reveals that degenerate explanations can be maliciously planted (allowing an attacker to hide the use of sensitive attributes) and can also emerge naturally, highlighting the need for reliable auditing. To address this, we introduce a novel faithfulness metric that reliably marks degenerate explanations as unfaithful, in both malicious and natural settings. Our code is available in the supplemental.

Is BatchEnsemble a Single Model? On Calibration and Diversity of Efficient Ensembles

In resource-constrained and low-latency settings, uncertainty estimates must be efficiently obtained. Deep Ensembles provide robust epistemic uncertainty (EU) but require training multiple full-size models. BatchEnsemble aims to deliver ensemble-like EU at far lower parameter and memory cost by applying learned rank-1 perturbations to a shared base network. We show that BatchEnsemble not only underperforms Deep Ensembles but closely tracks a single model baseline in terms of accuracy, calibration and out-of-distribution (OOD) detection on CIFAR10/10C/SVHN. A controlled study on MNIST finds members are near-identical in function and parameter space, indicating limited capacity to realize distinct predictive modes. Thus, BatchEnsemble behaves more like a single model than a true ensemble.

Probably Approximately Global Robustness Certification

We propose and investigate probabilistic guarantees for the adversarial robustness of classification algorithms. While traditional formal verification approaches for robustness are intractable and sampling-based approaches do not provide formal guarantees, our approach is able to efficiently certify a probabilistic relaxation of robustness. The key idea is to sample an $ε$-net and invoke a local robustness oracle on the sample. Remarkably, the size of the sample needed to achieve probably approximately global robustness guarantees is independent of the input dimensionality, the number of classes, and the learning algorithm itself. Our approach can, therefore, be applied even to large neural networks that are beyond the scope of traditional formal verification. Experiments empirically confirm that it characterizes robustness better than state-of-the-art sampling-based approaches and scales better than formal methods.

Beyond Topological Self-Explainable GNNs: A Formal Explainability Perspective

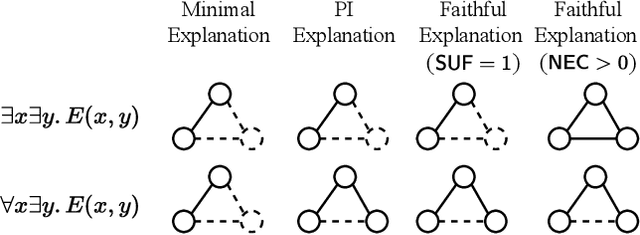
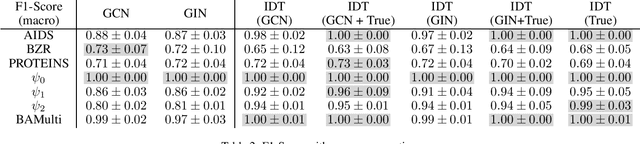
Self-Explainable Graph Neural Networks (SE-GNNs) are popular explainable-by-design GNNs, but the properties and the limitations of their explanations are not well understood. Our first contribution fills this gap by formalizing the explanations extracted by SE-GNNs, referred to as Trivial Explanations (TEs), and comparing them to established notions of explanations, namely Prime Implicant (PI) and faithful explanations. Our analysis reveals that TEs match PI explanations for a restricted but significant family of tasks. In general, however, they can be less informative than PI explanations and are surprisingly misaligned with widely accepted notions of faithfulness. Although faithful and PI explanations are informative, they are intractable to find and we show that they can be prohibitively large. Motivated by this, we propose Dual-Channel GNNs that integrate a white-box rule extractor and a standard SE-GNN, adaptively combining both channels when the task benefits. Our experiments show that even a simple instantiation of Dual-Channel GNNs can recover succinct rules and perform on par or better than widely used SE-GNNs. Our code can be found in the supplementary material.

Logical Distillation of Graph Neural Networks

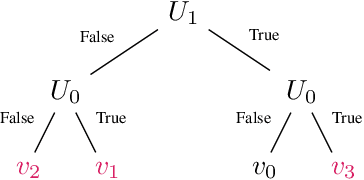
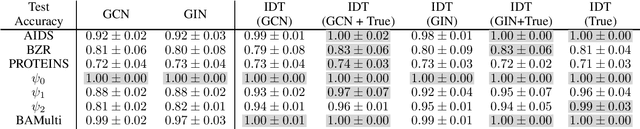
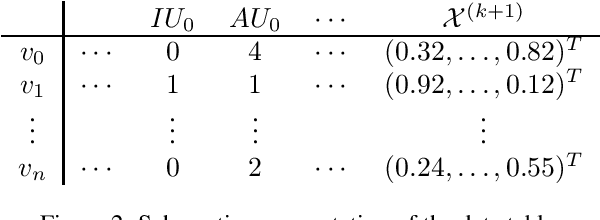
We present a logic based interpretable model for learning on graphs and an algorithm to distill this model from a Graph Neural Network (GNN). Recent results have shown connections between the expressivity of GNNs and the two-variable fragment of first-order logic with counting quantifiers (C2). We introduce a decision-tree based model which leverages an extension of C2 to distill interpretable logical classifiers from GNNs. We test our approach on multiple GNN architectures. The distilled models are interpretable, succinct, and attain similar accuracy to the underlying GNN. Furthermore, when the ground truth is expressible in C2, our approach outperforms the GNN.

Understanding Domain-Size Generalization in Markov Logic Networks

We study the generalization behavior of Markov Logic Networks (MLNs) across relational structures of different sizes. Multiple works have noticed that MLNs learned on a given domain generalize poorly across domains of different sizes. This behavior emerges from a lack of internal consistency within an MLN when used across different domain sizes. In this paper, we quantify this inconsistency and bound it in terms of the variance of the MLN parameters. The parameter variance also bounds the KL divergence between an MLN's marginal distributions taken from different domain sizes. We use these bounds to show that maximizing the data log-likelihood while simultaneously minimizing the parameter variance corresponds to two natural notions of generalization across domain sizes. Our theoretical results apply to Exponential Random Graphs and other Markov network based relational models. Finally, we observe that solutions known to decrease the variance of the MLN parameters, like regularization and Domain-Size Aware MLNs, increase the internal consistency of the MLNs. We empirically verify our results on four different datasets, with different methods to control parameter variance, showing that controlling parameter variance leads to better generalization.

Simple and Effective Transfer Learning for Neuro-Symbolic Integration

Deep Learning (DL) techniques have achieved remarkable successes in recent years. However, their ability to generalize and execute reasoning tasks remains a challenge. A potential solution to this issue is Neuro-Symbolic Integration (NeSy), where neural approaches are combined with symbolic reasoning. Most of these methods exploit a neural network to map perceptions to symbols and a logical reasoner to predict the output of the downstream task. These methods exhibit superior generalization capacity compared to fully neural architectures. However, they suffer from several issues, including slow convergence, learning difficulties with complex perception tasks, and convergence to local minima. This paper proposes a simple yet effective method to ameliorate these problems. The key idea involves pretraining a neural model on the downstream task. Then, a NeSy model is trained on the same task via transfer learning, where the weights of the perceptual part are injected from the pretrained network. The key observation of our work is that the neural network fails to generalize only at the level of the symbolic part while being perfectly capable of learning the mapping from perceptions to symbols. We have tested our training strategy on various SOTA NeSy methods and datasets, demonstrating consistent improvements in the aforementioned problems.

Lifted Inference beyond First-Order Logic

Weighted First Order Model Counting (WFOMC) is fundamental to probabilistic inference in statistical relational learning models. As WFOMC is known to be intractable in general ($\#$P-complete), logical fragments that admit polynomial time WFOMC are of significant interest. Such fragments are called domain liftable. Recent works have shown that the two-variable fragment of first order logic extended with counting quantifiers ($\mathrm{C^2}$) is domain-liftable. However, many properties of real-world data, like acyclicity in citation networks and connectivity in social networks, cannot be modeled in $\mathrm{C^2}$, or first order logic in general. In this work, we expand the domain liftability of $\mathrm{C^2}$ with multiple such properties. We show that any $\mathrm{C^2}$ sentence remains domain liftable when one of its relations is restricted to represent a directed acyclic graph, a connected graph, a tree (resp. a directed tree) or a forest (resp. a directed forest). All our results rely on a novel and general methodology of "counting by splitting". Besides their application to probabilistic inference, our results provide a general framework for counting combinatorial structures. We expand a vast array of previous results in discrete mathematics literature on directed acyclic graphs, phylogenetic networks, etc.

Weighted First Order Model Counting with Directed Acyclic Graph Axioms

Weighted First Order Model Counting (WFOMC) is the task of computing the weighted sum of the models of a first-order logic sentence. Probabilistic inference problems in many statistical relational learning frameworks can be cast as a WFOMC problem. However, in general, WFOMC is known to be intractable (#P_1- complete). Hence, logical fragments that admit polynomial time WFOMC are of significant interest. Such fragments are called domain liftable. Recent works have identified the two-variable fragment of first-order logic, extended with counting quantifiers, to be domain liftable. In this paper, we extend this fragment with a Directed Acyclic Graph axiom, i.e., a relation is interpreted as a Directed Acyclic Graph.

Deep Symbolic Learning: Discovering Symbols and Rules from Perceptions

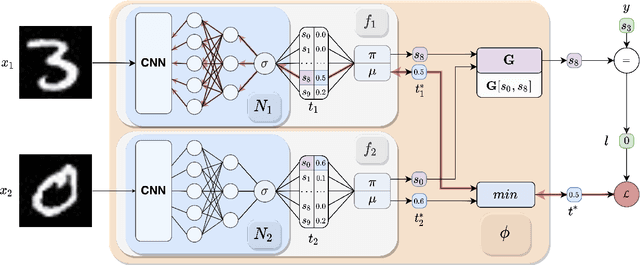
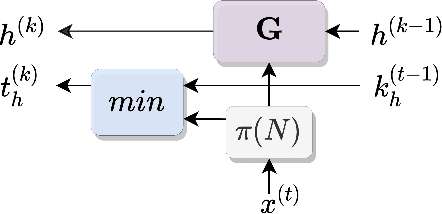
Neuro-Symbolic (NeSy) integration combines symbolic reasoning with Neural Networks (NNs) for tasks requiring perception and reasoning. Most NeSy systems rely on continuous relaxation of logical knowledge and no discrete decisions are made within the model pipeline. Furthermore, these methods assume that the symbolic rules are given. In this paper, we propose Deep Symbolic Learning (DSL), a NeSy system that learns NeSy-functions, i.e., the composition of a (set of) perception functions which map continuous data to discrete symbols, and a symbolic function over the set of symbols. DSL learns simultaneously the perception and symbolic functions, while being trained only on their composition (NeSy-function). The key novelty of DSL is that it can create internal (interpretable) symbolic representations and map them to perception inputs within a differentiable NN learning pipeline. The created symbols are automatically selected to generate symbolic functions that best explain the data. We provide experimental analysis to substantiate the efficacy of DSL in simultaneously learning perception and symbolic functions.