Beyond Topological Self-Explainable GNNs: A Formal Explainability Perspective

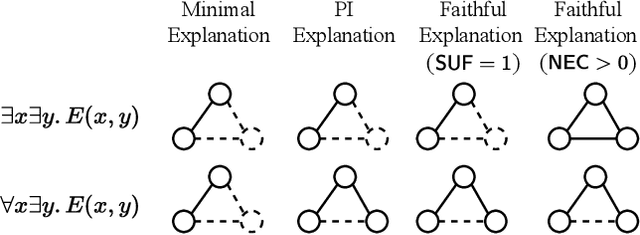
Self-Explainable Graph Neural Networks (SE-GNNs) are popular explainable-by-design GNNs, but the properties and the limitations of their explanations are not well understood. Our first contribution fills this gap by formalizing the explanations extracted by SE-GNNs, referred to as Trivial Explanations (TEs), and comparing them to established notions of explanations, namely Prime Implicant (PI) and faithful explanations. Our analysis reveals that TEs match PI explanations for a restricted but significant family of tasks. In general, however, they can be less informative than PI explanations and are surprisingly misaligned with widely accepted notions of faithfulness. Although faithful and PI explanations are informative, they are intractable to find and we show that they can be prohibitively large. Motivated by this, we propose Dual-Channel GNNs that integrate a white-box rule extractor and a standard SE-GNN, adaptively combining both channels when the task benefits. Our experiments show that even a simple instantiation of Dual-Channel GNNs can recover succinct rules and perform on par or better than widely used SE-GNNs. Our code can be found in the supplementary material.