Of Dice and Games: A Theory of Generalized Boosting

Cost-sensitive loss functions are crucial in many real-world prediction problems, where different types of errors are penalized differently; for example, in medical diagnosis, a false negative prediction can lead to worse consequences than a false positive prediction. However, traditional PAC learning theory has mostly focused on the symmetric 0-1 loss, leaving cost-sensitive losses largely unaddressed. In this work, we extend the celebrated theory of boosting to incorporate both cost-sensitive and multi-objective losses. Cost-sensitive losses assign costs to the entries of a confusion matrix, and are used to control the sum of prediction errors accounting for the cost of each error type. Multi-objective losses, on the other hand, simultaneously track multiple cost-sensitive losses, and are useful when the goal is to satisfy several criteria at once (e.g., minimizing false positives while keeping false negatives below a critical threshold). We develop a comprehensive theory of cost-sensitive and multi-objective boosting, providing a taxonomy of weak learning guarantees that distinguishes which guarantees are trivial (i.e., can always be achieved), which ones are boostable (i.e., imply strong learning), and which ones are intermediate, implying non-trivial yet not arbitrarily accurate learning. For binary classification, we establish a dichotomy: a weak learning guarantee is either trivial or boostable. In the multiclass setting, we describe a more intricate landscape of intermediate weak learning guarantees. Our characterization relies on a geometric interpretation of boosting, revealing a surprising equivalence between cost-sensitive and multi-objective losses.

Self-Directed Learning of Convex Labelings on Graphs

We study the problem of learning the clusters of a given graph in the self-directed learning setup. This learning setting is a variant of online learning, where rather than an adversary determining the sequence in which nodes are presented, the learner autonomously and adaptively selects them. While self-directed learning of Euclidean halfspaces, linear functions, and general abstract multi-class hypothesis classes was recently considered, no results previously existed specifically for self-directed node classification on graphs. In this paper, we address this problem developing efficient algorithms for it. More specifically, we focus on the case of (geodesically) convex clusters, i.e., for every two nodes sharing the same label, all nodes on every shortest path between them also share the same label. In particular, we devise a polynomial-time algorithm that makes only $3(h(G)+1)^4 \ln n$ mistakes on graphs with two convex clusters, where $n$ is the total number of nodes and $h(G)$ is the Hadwiger number, i.e., the size of the largest clique minor of the graph $G$. We also show that our algorithm is robust to the case that clusters are slightly non-convex, still achieving a mistake bound logarithmic in $n$. Finally, for the more standard case of homophilic clusters, where strongly connected nodes tend to belong the same class, we devise a simple and efficient algorithm.

A Theory of Interpretable Approximations

Can a deep neural network be approximated by a small decision tree based on simple features? This question and its variants are behind the growing demand for machine learning models that are *interpretable* by humans. In this work we study such questions by introducing *interpretable approximations*, a notion that captures the idea of approximating a target concept $c$ by a small aggregation of concepts from some base class $\mathcal{H}$. In particular, we consider the approximation of a binary concept $c$ by decision trees based on a simple class $\mathcal{H}$ (e.g., of bounded VC dimension), and use the tree depth as a measure of complexity. Our primary contribution is the following remarkable trichotomy. For any given pair of $\mathcal{H}$ and $c$, exactly one of these cases holds: (i) $c$ cannot be approximated by $\mathcal{H}$ with arbitrary accuracy; (ii) $c$ can be approximated by $\mathcal{H}$ with arbitrary accuracy, but there exists no universal rate that bounds the complexity of the approximations as a function of the accuracy; or (iii) there exists a constant $\kappa$ that depends only on $\mathcal{H}$ and $c$ such that, for *any* data distribution and *any* desired accuracy level, $c$ can be approximated by $\mathcal{H}$ with a complexity not exceeding $\kappa$. This taxonomy stands in stark contrast to the landscape of supervised classification, which offers a complex array of distribution-free and universally learnable scenarios. We show that, in the case of interpretable approximations, even a slightly nontrivial a-priori guarantee on the complexity of approximations implies approximations with constant (distribution-free and accuracy-free) complexity. We extend our trichotomy to classes $\mathcal{H}$ of unbounded VC dimension and give characterizations of interpretability based on the algebra generated by $\mathcal{H}$.

Efficient Algorithms for Learning Monophonic Halfspaces in Graphs

We study the problem of learning a binary classifier on the vertices of a graph. In particular, we consider classifiers given by monophonic halfspaces, partitions of the vertices that are convex in a certain abstract sense. Monophonic halfspaces, and related notions such as geodesic halfspaces,have recently attracted interest, and several connections have been drawn between their properties(e.g., their VC dimension) and the structure of the underlying graph $G$. We prove several novel results for learning monophonic halfspaces in the supervised, online, and active settings. Our main result is that a monophonic halfspace can be learned with near-optimal passive sample complexity in time polynomial in $n = |V(G)|$. This requires us to devise a polynomial-time algorithm for consistent hypothesis checking, based on several structural insights on monophonic halfspaces and on a reduction to $2$-satisfiability. We prove similar results for the online and active settings. We also show that the concept class can be enumerated with delay $\operatorname{poly}(n)$, and that empirical risk minimization can be performed in time $2^{\omega(G)}\operatorname{poly}(n)$ where $\omega(G)$ is the clique number of $G$. These results answer open questions from the literature (Gonz\'alez et al., 2020), and show a contrast with geodesic halfspaces, for which some of the said problems are NP-hard (Seiffarth et al., 2023).

Bandits with Abstention under Expert Advice

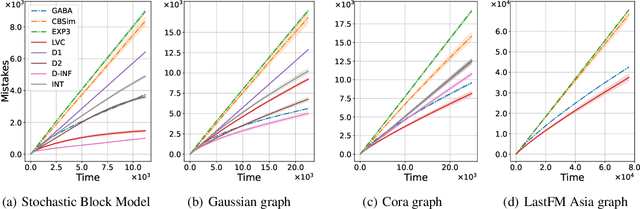
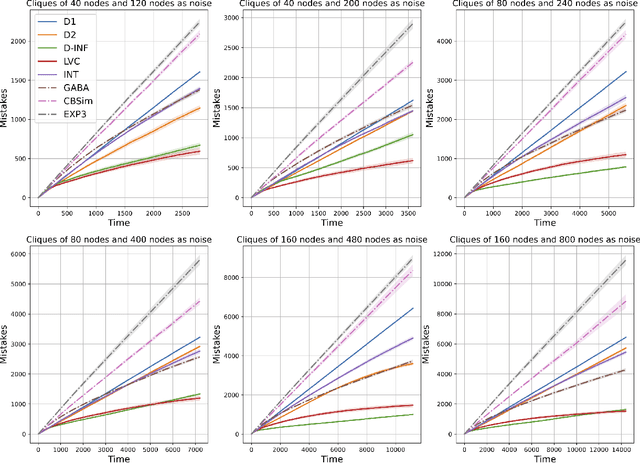
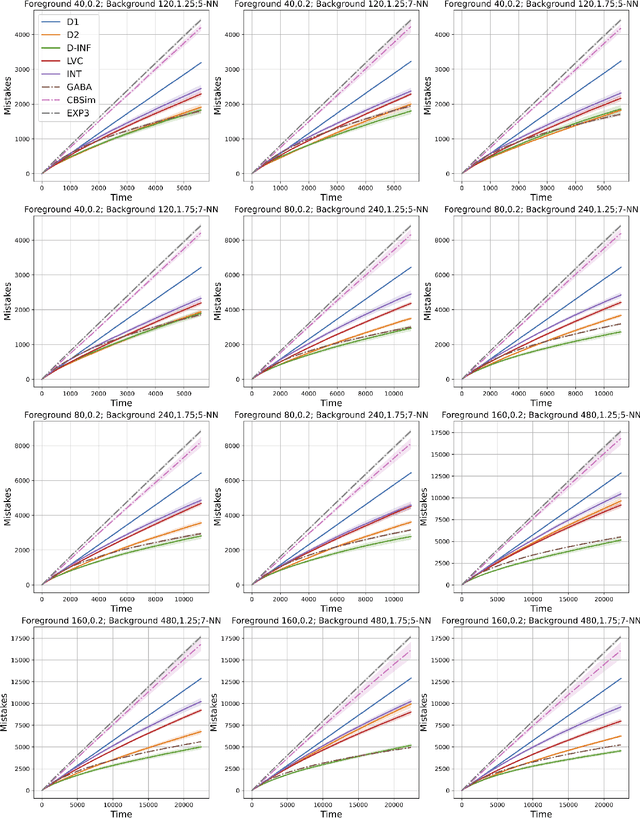
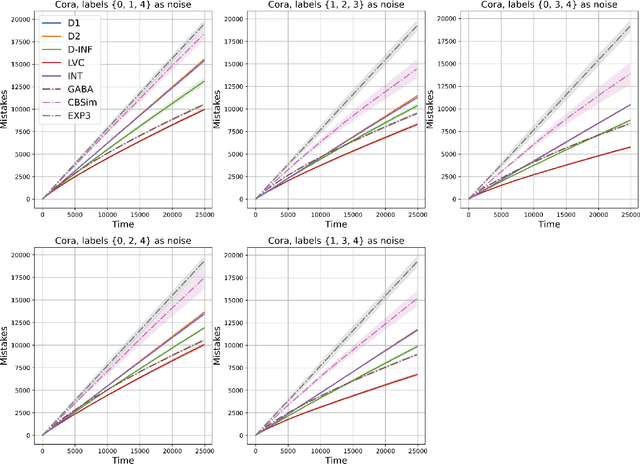
We study the classic problem of prediction with expert advice under bandit feedback. Our model assumes that one action, corresponding to the learner's abstention from play, has no reward or loss on every trial. We propose the CBA algorithm, which exploits this assumption to obtain reward bounds that can significantly improve those of the classical Exp4 algorithm. We can view our problem as the aggregation of confidence-rated predictors when the learner has the option of abstention from play. Importantly, we are the first to achieve bounds on the expected cumulative reward for general confidence-rated predictors. In the special case of specialists we achieve a novel reward bound, significantly improving previous bounds of SpecialistExp (treating abstention as another action). As an example application, we discuss learning unions of balls in a finite metric space. In this contextual setting, we devise an efficient implementation of CBA, reducing the runtime from quadratic to almost linear in the number of contexts. Preliminary experiments show that CBA improves over existing bandit algorithms.

Expectation-Complete Graph Representations with Homomorphisms

We investigate novel random graph embeddings that can be computed in expected polynomial time and that are able to distinguish all non-isomorphic graphs in expectation. Previous graph embeddings have limited expressiveness and either cannot distinguish all graphs or cannot be computed efficiently for every graph. To be able to approximate arbitrary functions on graphs, we are interested in efficient alternatives that become arbitrarily expressive with increasing resources. Our approach is based on Lov\'asz' characterisation of graph isomorphism through an infinite dimensional vector of homomorphism counts. Our empirical evaluation shows competitive results on several benchmark graph learning tasks.

Generalized Laplacian Positional Encoding for Graph Representation Learning

Graph neural networks (GNNs) are the primary tool for processing graph-structured data. Unfortunately, the most commonly used GNNs, called Message Passing Neural Networks (MPNNs) suffer from several fundamental limitations. To overcome these limitations, recent works have adapted the idea of positional encodings to graph data. This paper draws inspiration from the recent success of Laplacian-based positional encoding and defines a novel family of positional encoding schemes for graphs. We accomplish this by generalizing the optimization problem that defines the Laplace embedding to more general dissimilarity functions rather than the 2-norm used in the original formulation. This family of positional encodings is then instantiated by considering p-norms. We discuss a method for calculating these positional encoding schemes, implement it in PyTorch and demonstrate how the resulting positional encoding captures different properties of the graph. Furthermore, we demonstrate that this novel family of positional encodings can improve the expressive power of MPNNs. Lastly, we present preliminary experimental results.

Active Learning of Classifiers with Label and Seed Queries

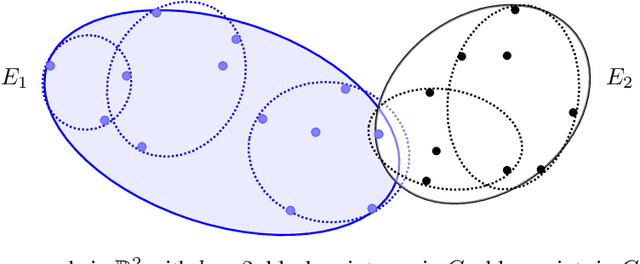
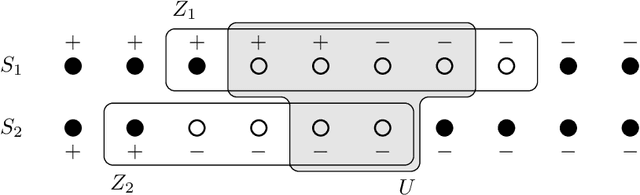
We study exact active learning of binary and multiclass classifiers with margin. Given an $n$-point set $X \subset \mathbb{R}^m$, we want to learn any unknown classifier on $X$ whose classes have finite strong convex hull margin, a new notion extending the SVM margin. In the standard active learning setting, where only label queries are allowed, learning a classifier with strong convex hull margin $\gamma$ requires in the worst case $\Omega\big(1+\frac{1}{\gamma}\big)^{(m-1)/2}$ queries. On the other hand, using the more powerful seed queries (a variant of equivalence queries), the target classifier could be learned in $O(m \log n)$ queries via Littlestone's Halving algorithm; however, Halving is computationally inefficient. In this work we show that, by carefully combining the two types of queries, a binary classifier can be learned in time $\operatorname{poly}(n+m)$ using only $O(m^2 \log n)$ label queries and $O\big(m \log \frac{m}{\gamma}\big)$ seed queries; the result extends to $k$-class classifiers at the price of a $k!k^2$ multiplicative overhead. Similar results hold when the input points have bounded bit complexity, or when only one class has strong convex hull margin against the rest. We complement the upper bounds by showing that in the worst case any algorithm needs $\Omega\big(k m \log \frac{1}{\gamma}\big)$ seed and label queries to learn a $k$-class classifier with strong convex hull margin $\gamma$.