Of Dice and Games: A Theory of Generalized Boosting

Cost-sensitive loss functions are crucial in many real-world prediction problems, where different types of errors are penalized differently; for example, in medical diagnosis, a false negative prediction can lead to worse consequences than a false positive prediction. However, traditional PAC learning theory has mostly focused on the symmetric 0-1 loss, leaving cost-sensitive losses largely unaddressed. In this work, we extend the celebrated theory of boosting to incorporate both cost-sensitive and multi-objective losses. Cost-sensitive losses assign costs to the entries of a confusion matrix, and are used to control the sum of prediction errors accounting for the cost of each error type. Multi-objective losses, on the other hand, simultaneously track multiple cost-sensitive losses, and are useful when the goal is to satisfy several criteria at once (e.g., minimizing false positives while keeping false negatives below a critical threshold). We develop a comprehensive theory of cost-sensitive and multi-objective boosting, providing a taxonomy of weak learning guarantees that distinguishes which guarantees are trivial (i.e., can always be achieved), which ones are boostable (i.e., imply strong learning), and which ones are intermediate, implying non-trivial yet not arbitrarily accurate learning. For binary classification, we establish a dichotomy: a weak learning guarantee is either trivial or boostable. In the multiclass setting, we describe a more intricate landscape of intermediate weak learning guarantees. Our characterization relies on a geometric interpretation of boosting, revealing a surprising equivalence between cost-sensitive and multi-objective losses.

Multiclass Boosting: Simple and Intuitive Weak Learning Criteria

We study a generalization of boosting to the multiclass setting. We introduce a weak learning condition for multiclass classification that captures the original notion of weak learnability as being "slightly better than random guessing". We give a simple and efficient boosting algorithm, that does not require realizability assumptions and its sample and oracle complexity bounds are independent of the number of classes. In addition, we utilize our new boosting technique in several theoretical applications within the context of List PAC Learning. First, we establish an equivalence to weak PAC learning. Furthermore, we present a new result on boosting for list learners, as well as provide a novel proof for the characterization of multiclass PAC learning and List PAC learning. Notably, our technique gives rise to a simplified analysis, and also implies an improved error bound for large list sizes, compared to previous results.

A Unified Model and Dimension for Interactive Estimation

We study an abstract framework for interactive learning called interactive estimation in which the goal is to estimate a target from its "similarity'' to points queried by the learner. We introduce a combinatorial measure called dissimilarity dimension which largely captures learnability in our model. We present a simple, general, and broadly-applicable algorithm, for which we obtain both regret and PAC generalization bounds that are polynomial in the new dimension. We show that our framework subsumes and thereby unifies two classic learning models: statistical-query learning and structured bandits. We also delineate how the dissimilarity dimension is related to well-known parameters for both frameworks, in some cases yielding significantly improved analyses.

Projection-free Adaptive Regret with Membership Oracles

In the framework of online convex optimization, most iterative algorithms require the computation of projections onto convex sets, which can be computationally expensive. To tackle this problem HK12 proposed the study of projection-free methods that replace projections with less expensive computations. The most common approach is based on the Frank-Wolfe method, that uses linear optimization computation in lieu of projections. Recent work by GK22 gave sublinear adaptive regret guarantees with projection free algorithms based on the Frank Wolfe approach. In this work we give projection-free algorithms that are based on a different technique, inspired by Mhammedi22, that replaces projections by set-membership computations. We propose a simple lazy gradient-based algorithm with a Minkowski regularization that attains near-optimal adaptive regret bounds. For general convex loss functions we improve previous adaptive regret bounds from $O(T^{3/4})$ to $O(\sqrt{T})$, and further to tight interval dependent bound $\tilde{O}(\sqrt{I})$ where $I$ denotes the interval length. For strongly convex functions we obtain the first poly-logarithmic adaptive regret bounds using a projection-free algorithm.

A Characterization of Multiclass Learnability

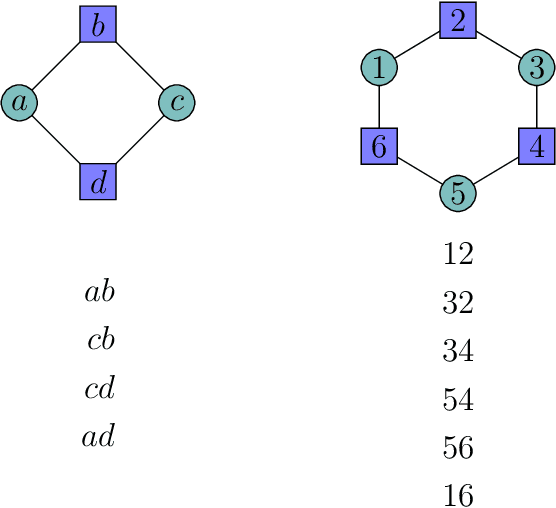
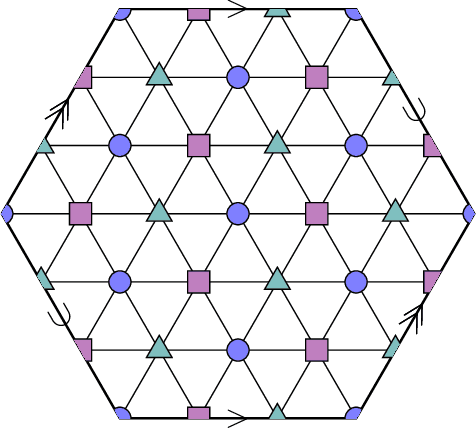
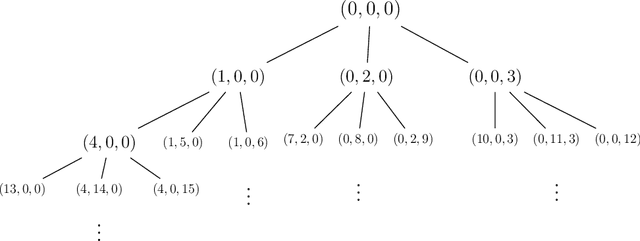
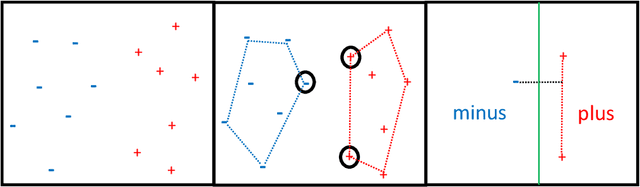
A seminal result in learning theory characterizes the PAC learnability of binary classes through the Vapnik-Chervonenkis dimension. Extending this characterization to the general multiclass setting has been open since the pioneering works on multiclass PAC learning in the late 1980s. This work resolves this problem: we characterize multiclass PAC learnability through the DS dimension, a combinatorial dimension defined by Daniely and Shalev-Shwartz (2014). The classical characterization of the binary case boils down to empirical risk minimization. In contrast, our characterization of the multiclass case involves a variety of algorithmic ideas; these include a natural setting we call list PAC learning. In the list learning setting, instead of predicting a single outcome for a given unseen input, the goal is to provide a short menu of predictions. Our second main result concerns the Natarajan dimension, which has been a central candidate for characterizing multiclass learnability. This dimension was introduced by Natarajan (1988) as a barrier for PAC learning. Whether the Natarajan dimension characterizes PAC learnability in general has been posed as an open question in several papers since. This work provides a negative answer: we construct a non-learnable class with Natarajan dimension one. For the construction, we identify a fundamental connection between concept classes and topology (i.e., colorful simplicial complexes). We crucially rely on a deep and involved construction of hyperbolic pseudo-manifolds by Januszkiewicz and Swiatkowski. It is interesting that hyperbolicity is directly related to learning problems that are difficult to solve although no obvious barriers exist. This is another demonstration of the fruitful links machine learning has with different areas in mathematics.

A Boosting Approach to Reinforcement Learning

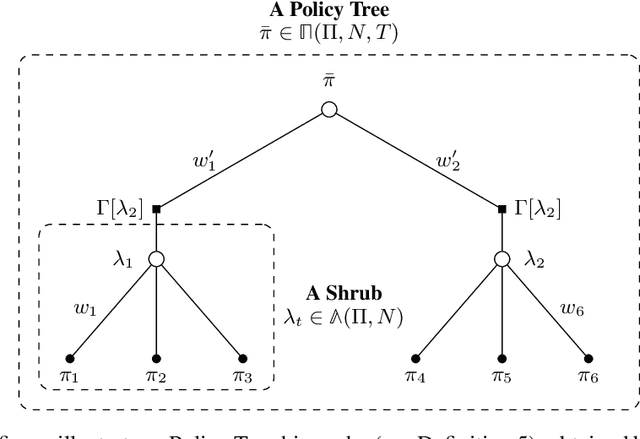
We study efficient algorithms for reinforcement learning in Markov decision processes whose complexity is independent of the number of states. This formulation succinctly captures large scale problems, but is also known to be computationally hard in its general form. Previous approaches attempt to circumvent the computational hardness by assuming structure in either transition function or the value function, or by relaxing the solution guarantee to a local optimality condition. We consider the methodology of boosting, borrowed from supervised learning, for converting weak learners into an accurate policy. The notion of weak learning we study is that of sampled-based approximate optimization of linear functions over policies. Under this assumption of weak learnability, we give an efficient algorithm that is capable of improving the accuracy of such weak learning methods, till global optimality is reached. We prove sample complexity and running time bounds on our method, that are polynomial in the natural parameters of the problem: approximation guarantee, discount factor, distribution mismatch and number of actions. In particular, our bound does not depend on the number of states. A technical difficulty in applying previous boosting results, is that the value function over policy space is not convex. We show how to use a non-convex variant of the Frank-Wolfe method, coupled with recent advances in gradient boosting that allow incorporating a weak learner with multiplicative approximation guarantee, to overcome the non-convexity and attain global convergence.

Online Boosting with Bandit Feedback

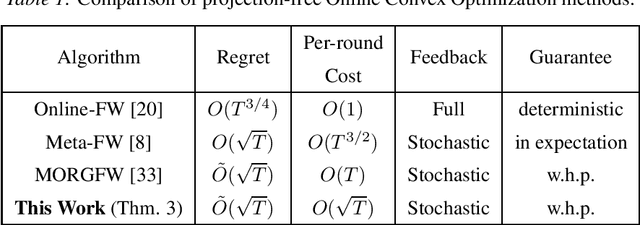
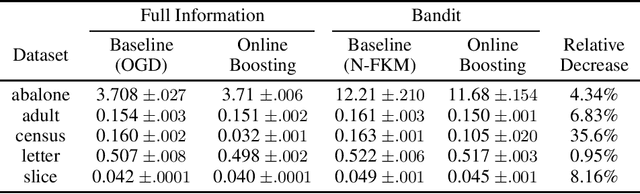
We consider the problem of online boosting for regression tasks, when only limited information is available to the learner. We give an efficient regret minimization method that has two implications: an online boosting algorithm with noisy multi-point bandit feedback, and a new projection-free online convex optimization algorithm with stochastic gradient, that improves state-of-the-art guarantees in terms of efficiency.

Online Agnostic Boosting via Regret Minimization

Boosting is a widely used machine learning approach based on the idea of aggregating weak learning rules. While in statistical learning numerous boosting methods exist both in the realizable and agnostic settings, in online learning they exist only in the realizable case. In this work we provide the first agnostic online boosting algorithm; that is, given a weak learner with only marginally-better-than-trivial regret guarantees, our algorithm boosts it to a strong learner with sublinear regret. Our algorithm is based on an abstract (and simple) reduction to online convex optimization, which efficiently converts an arbitrary online convex optimizer to an online booster. Moreover, this reduction extends to the statistical as well as the online realizable settings, thus unifying the 4 cases of statistical/online and agnostic/realizable boosting.

Boosting for Dynamical Systems

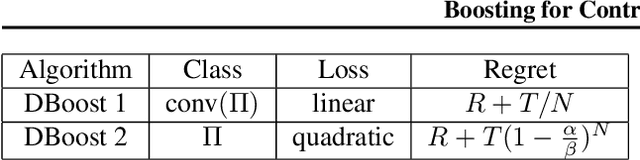
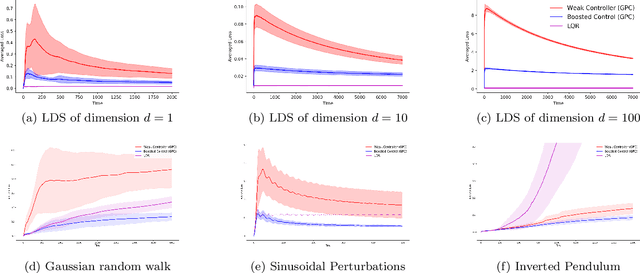
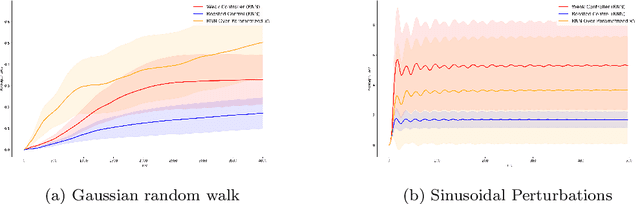
We propose a framework of boosting for learning and control in environments that maintain a state. Leveraging methods for online learning with memory and for online boosting, we design an efficient online algorithm that can provably improve the accuracy of weak-learners in stateful environments. As a consequence, we give efficient boosting algorithms for both prediction and the control of dynamical systems. Empirical evaluation on simulated and real data for both control and prediction supports our theoretical findings.

Following High-level Navigation Instructions on a Simulated Quadcopter with Imitation Learning

We introduce a method for following high-level navigation instructions by mapping directly from images, instructions and pose estimates to continuous low-level velocity commands for real-time control. The Grounded Semantic Mapping Network (GSMN) is a fully-differentiable neural network architecture that builds an explicit semantic map in the world reference frame by incorporating a pinhole camera projection model within the network. The information stored in the map is learned from experience, while the local-to-world transformation is computed explicitly. We train the model using DAggerFM, a modified variant of DAgger that trades tabular convergence guarantees for improved training speed and memory use. We test GSMN in virtual environments on a realistic quadcopter simulator and show that incorporating an explicit mapping and grounding modules allows GSMN to outperform strong neural baselines and almost reach an expert policy performance. Finally, we analyze the learned map representations and show that using an explicit map leads to an interpretable instruction-following model.