A Unified Model and Dimension for Interactive Estimation

We study an abstract framework for interactive learning called interactive estimation in which the goal is to estimate a target from its "similarity'' to points queried by the learner. We introduce a combinatorial measure called dissimilarity dimension which largely captures learnability in our model. We present a simple, general, and broadly-applicable algorithm, for which we obtain both regret and PAC generalization bounds that are polynomial in the new dimension. We show that our framework subsumes and thereby unifies two classic learning models: statistical-query learning and structured bandits. We also delineate how the dissimilarity dimension is related to well-known parameters for both frameworks, in some cases yielding significantly improved analyses.

Interactive Learning from Activity Description

We present a novel interactive learning protocol that enables training request-fulfilling agents by verbally describing their activities. Our protocol gives rise to a new family of interactive learning algorithms that offer complementary advantages against traditional algorithms like imitation learning (IL) and reinforcement learning (RL). We develop an algorithm that practically implements this protocol and employ it to train agents in two challenging request-fulfilling problems using purely language-description feedback. Empirical results demonstrate the strengths of our algorithm: compared to RL baselines, it is more sample-efficient; compared to IL baselines, it achieves competitive success rates while not requiring feedback providers to have agent-specific expertise. We also provide theoretical guarantees of the algorithm under certain assumptions on the teacher and the environment.

Reinforcement Learning with Convex Constraints

In standard reinforcement learning (RL), a learning agent seeks to optimize the overall reward. However, many key aspects of a desired behavior are more naturally expressed as constraints. For instance, the designer may want to limit the use of unsafe actions, increase the diversity of trajectories to enable exploration, or approximate expert trajectories when rewards are sparse. In this paper, we propose an algorithmic scheme that can handle a wide class of constraints in RL tasks: specifically, any constraints that require expected values of some vector measurements (such as the use of an action) to lie in a convex set. This captures previously studied constraints (such as safety and proximity to an expert), but also enables new classes of constraints (such as diversity). Our approach comes with rigorous theoretical guarantees and only relies on the ability to approximately solve standard RL tasks. As a result, it can be easily adapted to work with any model-free or model-based RL. In our experiments, we show that it matches previous algorithms that enforce safety via constraints, but can also enforce new properties that these algorithms do not incorporate, such as diversity.

Adversarial Bandits with Knapsacks

We consider Bandits with Knapsacks (henceforth, BwK), a general model for multi-armed bandits under supply/budget constraints. In particular, a bandit algorithm needs to solve a well-known knapsack problem: find an optimal packing of items into a limited-size knapsack. The BwK problem is a common generalization of numerous motivating examples, which range from dynamic pricing to repeated auctions to dynamic ad allocation to network routing and scheduling. While the prior work on BwK focused on the stochastic version, we pioneer the other extreme in which the outcomes can be chosen adversarially. This is a considerably harder problem, compared to both the stochastic version and the "classic" adversarial bandits, in that regret minimization is no longer feasible. Instead, the objective is to minimize the competitive ratio: the ratio of the benchmark reward to the algorithm's reward. We design an algorithm with competitive ratio O(log T) relative to the best fixed distribution over actions, where T is the time horizon; we also prove a matching lower bound. The key conceptual contribution is a new perspective on the stochastic version of the problem. We suggest a new algorithm for the stochastic version, which builds on the framework of regret minimization in repeated games and admits a substantially simpler analysis compared to prior work. We then analyze this algorithm for the adversarial version and use it as a subroutine to solve the latter.

Learning Deep ResNet Blocks Sequentially using Boosting Theory

Deep neural networks are known to be difficult to train due to the instability of back-propagation. A deep \emph{residual network} (ResNet) with identity loops remedies this by stabilizing gradient computations. We prove a boosting theory for the ResNet architecture. We construct $T$ weak module classifiers, each contains two of the $T$ layers, such that the combined strong learner is a ResNet. Therefore, we introduce an alternative Deep ResNet training algorithm, \emph{BoostResNet}, which is particularly suitable in non-differentiable architectures. Our proposed algorithm merely requires a sequential training of $T$ "shallow ResNets" which are inexpensive. We prove that the training error decays exponentially with the depth $T$ if the \emph{weak module classifiers} that we train perform slightly better than some weak baseline. In other words, we propose a weak learning condition and prove a boosting theory for ResNet under the weak learning condition. Our results apply to general multi-class ResNets. A generalization error bound based on margin theory is proved and suggests ResNet's resistant to overfitting under network with $l_1$ norm bounded weights.

Functional Frank-Wolfe Boosting for General Loss Functions

Boosting is a generic learning method for classification and regression. Yet, as the number of base hypotheses becomes larger, boosting can lead to a deterioration of test performance. Overfitting is an important and ubiquitous phenomenon, especially in regression settings. To avoid overfitting, we consider using $l_1$ regularization. We propose a novel Frank-Wolfe type boosting algorithm (FWBoost) applied to general loss functions. By using exponential loss, the FWBoost algorithm can be rewritten as a variant of AdaBoost for binary classification. FWBoost algorithms have exactly the same form as existing boosting methods, in terms of making calls to a base learning algorithm with different weights update. This direct connection between boosting and Frank-Wolfe yields a new algorithm that is as practical as existing boosting methods but with new guarantees and rates of convergence. Experimental results show that the test performance of FWBoost is not degraded with larger rounds in boosting, which is consistent with the theoretical analysis.

Convex Risk Minimization and Conditional Probability Estimation

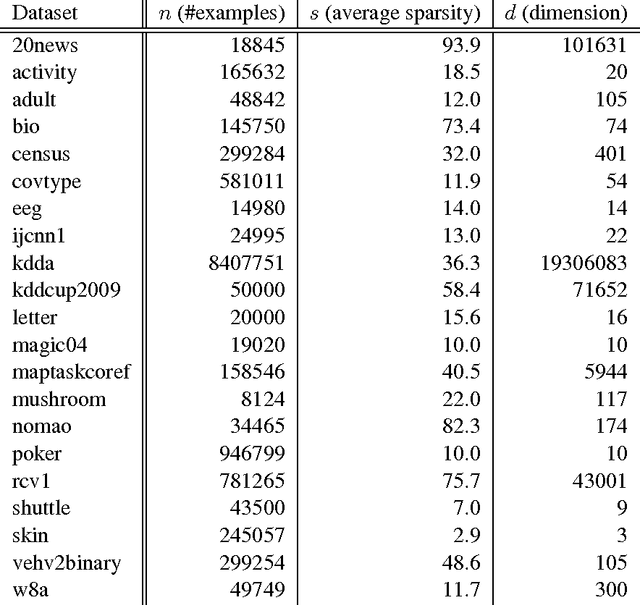
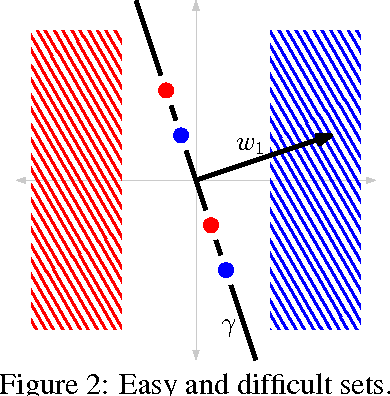
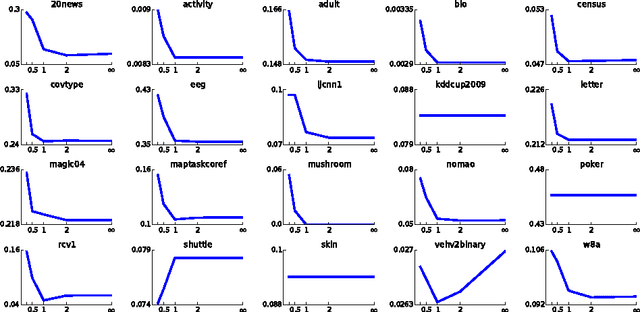
This paper proves, in very general settings, that convex risk minimization is a procedure to select a unique conditional probability model determined by the classification problem. Unlike most previous work, we give results that are general enough to include cases in which no minimum exists, as occurs typically, for instance, with standard boosting algorithms. Concretely, we first show that any sequence of predictors minimizing convex risk over the source distribution will converge to this unique model when the class of predictors is linear (but potentially of infinite dimension). Secondly, we show the same result holds for \emph{empirical} risk minimization whenever this class of predictors is finite dimensional, where the essential technical contribution is a norm-free generalization bound.