Zhou Lu
Augmented Affine Frequency Division Multiplexing for Both Low PAPR Signaling and Diversity Gain Protection
Dec 19, 2025
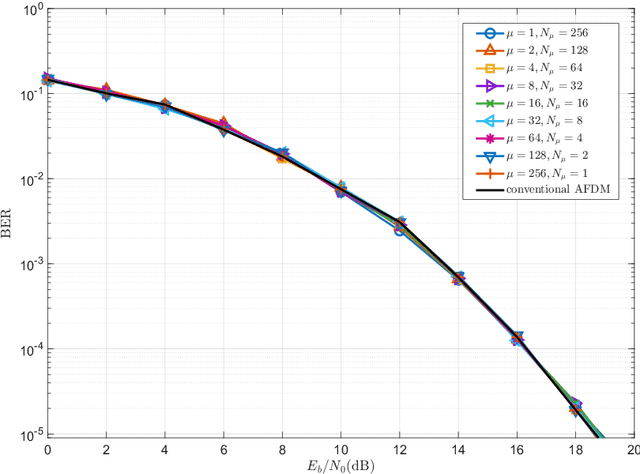
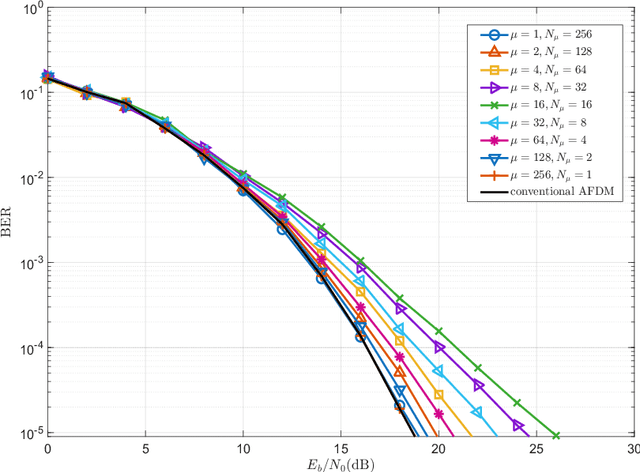
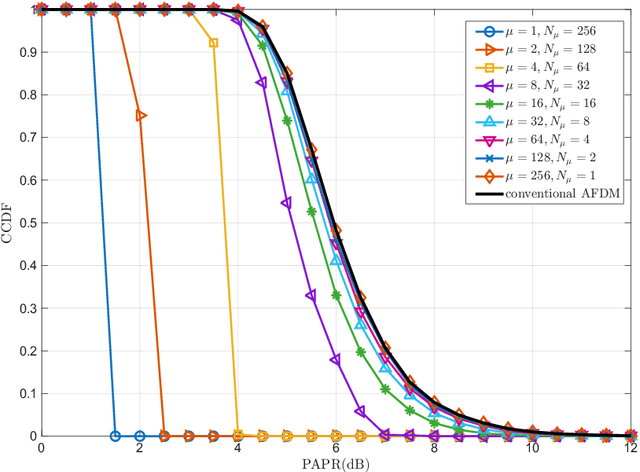
Abstract:Research results on Affine Frequency Division Multiplexing (AFDM) reveal that it experiences the same Peak-to-Average Power Ratio (PAPR) problem as conventional Orthogonal Frequency-Division Multiplexing (OFDM). On the other side, some references and also our studies demonstrate that AFDM involves an unneeded matrix, which is based on a parameter typically represented by $c_2$, for signalling. Hence, in this paper, an augmented AFDM scheme, referred to as A$^2$FDM, is proposed to mitigate the PAPR problem of AFDM, which is achieved by replacing the $c_2$ matrix in AFDM by a new unitary matrix that performs both sub-block-based Discrete Fourier Transform (DFT) and symbol mapping. Two symbol mapping schemes, namely interleaved mapping and localized mapping, are proposed for implementing A$^2$FDM, yielding the Interleaved A$^2$FDM and Localized A$^2$FDM. The input-output relationships of these schemes are derived and the complexity and the effects of system parameters on the performance of A$^2$FDM along with AFDM systems are analyzed. Furthermore, simulation results are provided to demonstrate and compare comprehensively the performance of the considered schemes in conjunction with different system settings and various operational conditions. Our studies and results demonstrate that, while A$^2$FDM is capable of circumventing the PAPR problem faced by AFDM, it is capable of attaining the achievable diversity gain, when AFDM is operated in its undesirable conditions resulting in the loss of the diversity gain available.
Population Dynamics Control with Partial Observations
Feb 19, 2025Abstract:We study the problem of controlling population dynamics, a class of linear dynamical systems evolving on the probability simplex, from the perspective of online non-stochastic control. While Golowich et.al. 2024 analyzed the fully observable setting, we focus on the more realistic, partially observable case, where only a low-dimensional representation of the state is accessible. In classical non-stochastic control, inputs are set as linear combinations of past disturbances. However, under partial observations, disturbances cannot be directly computed. To address this, Simchowitz et.al. 2020 proposed to construct oblivious signals, which are counterfactual observations with zero control, as a substitute. This raises several challenges in our setting: (1) how to construct oblivious signals under simplex constraints, where zero control is infeasible; (2) how to design a sufficiently expressive convex controller parameterization tailored to these signals; and (3) how to enforce the simplex constraint on control when projections may break the convexity of cost functions. Our main contribution is a new controller that achieves the optimal $\tilde{O}(\sqrt{T})$ regret with respect to a natural class of mixing linear dynamic controllers. To tackle these challenges, we construct signals based on hypothetical observations under a constant control adapted to the simplex domain, and introduce a new controller parameterization that approximates general control policies linear in non-oblivious observations. Furthermore, we employ a novel convex extension surrogate loss, inspired by Lattimore 2024, to bypass the projection-induced convexity issue.
Sparsity-Based Interpolation of External, Internal and Swap Regret
Feb 06, 2025
Abstract:Focusing on the expert problem in online learning, this paper studies the interpolation of several performance metrics via $\phi$-regret minimization, which measures the performance of an algorithm by its regret with respect to an arbitrary action modification rule $\phi$. With $d$ experts and $T\gg d$ rounds in total, we present a single algorithm achieving the instance-adaptive $\phi$-regret bound \begin{equation*} \tilde O\left(\min\left\{\sqrt{d-d^{\mathrm{unif}}_\phi+1},\sqrt{d-d^{\mathrm{self}}_\phi}\right\}\cdot\sqrt{T}\right), \end{equation*} where $d^{\mathrm{unif}}_\phi$ is the maximum amount of experts modified identically by $\phi$, and $d^{\mathrm{self}}_\phi$ is the amount of experts that $\phi$ trivially modifies to themselves. By recovering the optimal $O(\sqrt{T\log d})$ external regret bound when $d^{\mathrm{unif}}_\phi=d$, the standard $\tilde O(\sqrt{T})$ internal regret bound when $d^{\mathrm{self}}_\phi=d-1$ and the optimal $\tilde O(\sqrt{dT})$ swap regret bound in the worst case, we improve existing results in the intermediate regimes. In addition, the same algorithm achieves the optimal quantile regret bound, which corresponds to even easier settings of $\phi$ than the external regret. Building on the classical reduction from $\phi$-regret minimization to external regret minimization on stochastic matrices, our main idea is to further convert the latter to online linear regression using Haar-wavelet-inspired matrix features. Then, we apply a particular $L_1$-version of comparator-adaptive online learning algorithms to exploit the sparsity in this regression subroutine.
The Benefit of Being Bayesian in Online Conformal Prediction
Oct 03, 2024



Abstract:Based on the framework of Conformal Prediction (CP), we study the online construction of valid confidence sets given a black-box machine learning model. By converting the target confidence levels into quantile levels, the problem can be reduced to predicting the quantiles (in hindsight) of a sequentially revealed data sequence. Two very different approaches have been studied previously. (i) Direct approach: Assuming the data sequence is iid or exchangeable, one could maintain the empirical distribution of the observed data as an algorithmic belief, and directly predict its quantiles. (ii) Indirect approach: As statistical assumptions often do not hold in practice, a recent trend is to consider the adversarial setting and apply first-order online optimization to moving quantile losses (Gibbs & Cand\`es, 2021). It requires knowing the target quantile level beforehand, and suffers from certain validity issues on the obtained confidence sets, due to the associated loss linearization. This paper presents a novel Bayesian CP framework that combines their strengths. Without any statistical assumption, it is able to both: (i) answer multiple arbitrary confidence level queries online, with provably low regret; and (ii) overcome the validity issues suffered by first-order optimization baselines, due to being "data-centric" rather than "iterate-centric". From a technical perspective, our key idea is to regularize the algorithmic belief of the above direct approach by a Bayesian prior, which "robustifies" it by simulating a non-linearized Follow the Regularized Leader (FTRL) algorithm on the output. For statisticians, this can be regarded as an online adversarial view of Bayesian inference. Importantly, the proposed belief update backbone is shared by prediction heads targeting different confidence levels, bringing practical benefits analogous to U-calibration (Kleinberg et al., 2023).
Tight Rates for Bandit Control Beyond Quadratics
Oct 01, 2024Abstract:Unlike classical control theory, such as Linear Quadratic Control (LQC), real-world control problems are highly complex. These problems often involve adversarial perturbations, bandit feedback models, and non-quadratic, adversarially chosen cost functions. A fundamental yet unresolved question is whether optimal regret can be achieved for these general control problems. The standard approach to addressing this problem involves a reduction to bandit convex optimization with memory. In the bandit setting, constructing a gradient estimator with low variance is challenging due to the memory structure and non-quadratic loss functions. In this paper, we provide an affirmative answer to this question. Our main contribution is an algorithm that achieves an $\tilde{O}(\sqrt{T})$ optimal regret for bandit non-stochastic control with strongly-convex and smooth cost functions in the presence of adversarial perturbations, improving the previously known $\tilde{O}(T^{2/3})$ regret bound from (Cassel and Koren, 2020. Our algorithm overcomes the memory issue by reducing the problem to Bandit Convex Optimization (BCO) without memory and addresses general strongly-convex costs using recent advancements in BCO from (Suggala et al., 2024). Along the way, we develop an improved algorithm for BCO with memory, which may be of independent interest.
Online Control in Population Dynamics
Jun 03, 2024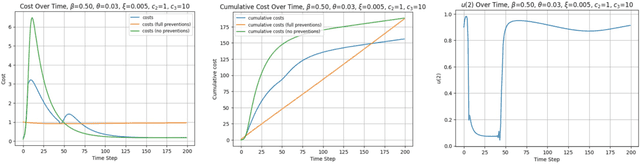
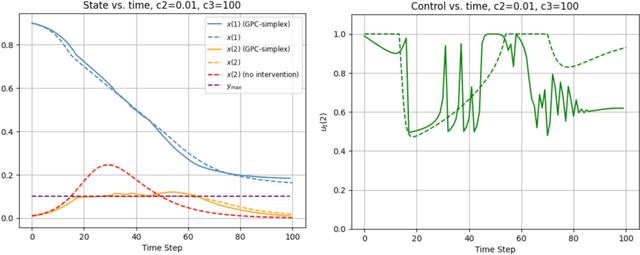
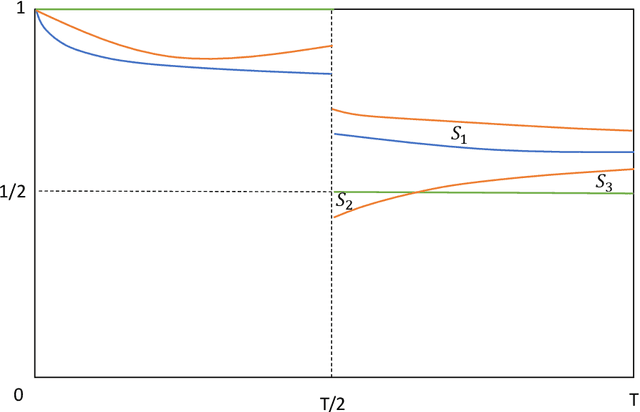
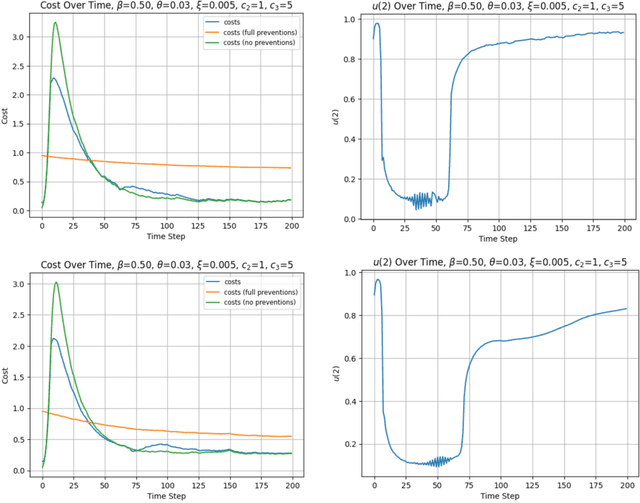
Abstract:The study of population dynamics originated with early sociological works (Malthus, 1872) but has since extended into many fields, including biology, epidemiology, evolutionary game theory, and economics. Most studies on population dynamics focus on the problem of prediction rather than control. Existing mathematical models for population control are often restricted to specific, noise-free dynamics, while real-world population changes can be complex and adversarial. To address this gap, we propose a new framework based on the paradigm of online control. We first characterize a set of linear dynamical systems that can naturally model evolving populations. We then give an efficient gradient-based controller for these systems, with near-optimal regret bounds with respect to a broad class of linear policies. Our empirical evaluations demonstrate the effectiveness of the proposed algorithm for population control even in non-linear models such as SIR and replicator dynamics.
Adaptive Regret for Bandits Made Possible: Two Queries Suffice
Jan 17, 2024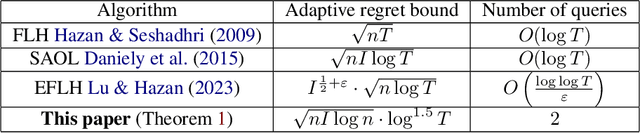
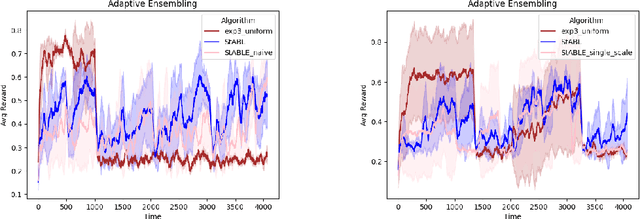
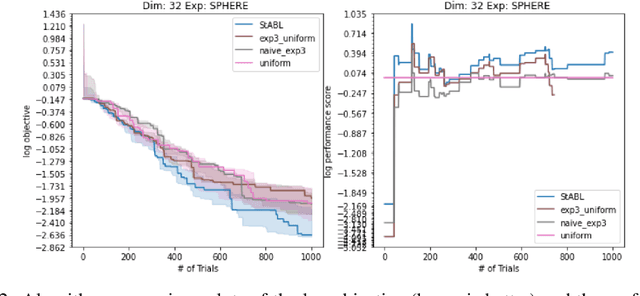
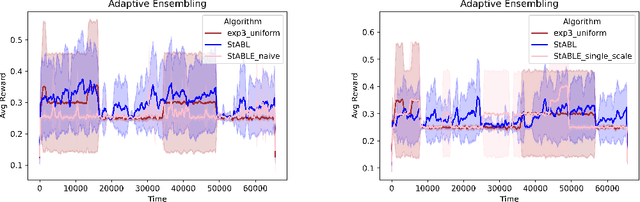
Abstract:Fast changing states or volatile environments pose a significant challenge to online optimization, which needs to perform rapid adaptation under limited observation. In this paper, we give query and regret optimal bandit algorithms under the strict notion of strongly adaptive regret, which measures the maximum regret over any contiguous interval $I$. Due to its worst-case nature, there is an almost-linear $\Omega(|I|^{1-\epsilon})$ regret lower bound, when only one query per round is allowed [Daniely el al, ICML 2015]. Surprisingly, with just two queries per round, we give Strongly Adaptive Bandit Learner (StABL) that achieves $\tilde{O}(\sqrt{n|I|})$ adaptive regret for multi-armed bandits with $n$ arms. The bound is tight and cannot be improved in general. Our algorithm leverages a multiplicative update scheme of varying stepsizes and a carefully chosen observation distribution to control the variance. Furthermore, we extend our results and provide optimal algorithms in the bandit convex optimization setting. Finally, we empirically demonstrate the superior performance of our algorithms under volatile environments and for downstream tasks, such as algorithm selection for hyperparameter optimization.
Non-uniform Online Learning: Towards Understanding Induction
Nov 30, 2023Abstract:Can a physicist make only finite errors in the endless pursuit of the law of nature? This millennium-old question of inductive inference is a fundamental, yet mysterious problem in philosophy, lacking rigorous justifications. While classic online learning theory and inductive inference share a similar sequential decision-making spirit, the former's reliance on an adaptive adversary and worst-case error bounds limits its applicability to the latter. In this work, we introduce the concept of non-uniform online learning, which we argue aligns more closely with the principles of inductive reasoning. This setting assumes a predetermined ground-truth hypothesis and considers non-uniform, hypothesis-wise error bounds. In the realizable setting, we provide a complete characterization of learnability with finite error: a hypothesis class is non-uniform learnable if and only if it's a countable union of Littlestone classes, no matter the observations are adaptively chosen or iid sampled. Additionally, we propose a necessary condition for the weaker criterion of consistency which we conjecture to be tight. To further promote our theory, we extend our result to the more realistic agnostic setting, showing that any countable union of Littlestone classes can be learnt with regret $\tilde{O}(\sqrt{T})$. We hope this work could offer a new perspective of interpreting the power of induction from an online learning viewpoint.
On the Computational Benefit of Multimodal Learning
Sep 25, 2023Abstract:Human perception inherently operates in a multimodal manner. Similarly, as machines interpret the empirical world, their learning processes ought to be multimodal. The recent, remarkable successes in empirical multimodal learning underscore the significance of understanding this paradigm. Yet, a solid theoretical foundation for multimodal learning has eluded the field for some time. While a recent study by Lu (2023) has shown the superior sample complexity of multimodal learning compared to its unimodal counterpart, another basic question remains: does multimodal learning also offer computational advantages over unimodal learning? This work initiates a study on the computational benefit of multimodal learning. We demonstrate that, under certain conditions, multimodal learning can outpace unimodal learning exponentially in terms of computation. Specifically, we present a learning task that is NP-hard for unimodal learning but is solvable in polynomial time by a multimodal algorithm. Our construction is based on a novel modification to the intersection of two half-spaces problem.
A Theory of Multimodal Learning
Sep 21, 2023Abstract:Human perception of the empirical world involves recognizing the diverse appearances, or 'modalities', of underlying objects. Despite the longstanding consideration of this perspective in philosophy and cognitive science, the study of multimodality remains relatively under-explored within the field of machine learning. Nevertheless, current studies of multimodal machine learning are limited to empirical practices, lacking theoretical foundations beyond heuristic arguments. An intriguing finding from the practice of multimodal learning is that a model trained on multiple modalities can outperform a finely-tuned unimodal model, even on unimodal tasks. This paper provides a theoretical framework that explains this phenomenon, by studying generalization properties of multimodal learning algorithms. We demonstrate that multimodal learning allows for a superior generalization bound compared to unimodal learning, up to a factor of $O(\sqrt{n})$, where $n$ represents the sample size. Such advantage occurs when both connection and heterogeneity exist between the modalities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge