Population Dynamics Control with Partial Observations

We study the problem of controlling population dynamics, a class of linear dynamical systems evolving on the probability simplex, from the perspective of online non-stochastic control. While Golowich et.al. 2024 analyzed the fully observable setting, we focus on the more realistic, partially observable case, where only a low-dimensional representation of the state is accessible. In classical non-stochastic control, inputs are set as linear combinations of past disturbances. However, under partial observations, disturbances cannot be directly computed. To address this, Simchowitz et.al. 2020 proposed to construct oblivious signals, which are counterfactual observations with zero control, as a substitute. This raises several challenges in our setting: (1) how to construct oblivious signals under simplex constraints, where zero control is infeasible; (2) how to design a sufficiently expressive convex controller parameterization tailored to these signals; and (3) how to enforce the simplex constraint on control when projections may break the convexity of cost functions. Our main contribution is a new controller that achieves the optimal $\tilde{O}(\sqrt{T})$ regret with respect to a natural class of mixing linear dynamic controllers. To tackle these challenges, we construct signals based on hypothetical observations under a constant control adapted to the simplex domain, and introduce a new controller parameterization that approximates general control policies linear in non-oblivious observations. Furthermore, we employ a novel convex extension surrogate loss, inspired by Lattimore 2024, to bypass the projection-induced convexity issue.

Sparsity-Based Interpolation of External, Internal and Swap Regret

Focusing on the expert problem in online learning, this paper studies the interpolation of several performance metrics via $\phi$-regret minimization, which measures the performance of an algorithm by its regret with respect to an arbitrary action modification rule $\phi$. With $d$ experts and $T\gg d$ rounds in total, we present a single algorithm achieving the instance-adaptive $\phi$-regret bound \begin{equation*} \tilde O\left(\min\left\{\sqrt{d-d^{\mathrm{unif}}_\phi+1},\sqrt{d-d^{\mathrm{self}}_\phi}\right\}\cdot\sqrt{T}\right), \end{equation*} where $d^{\mathrm{unif}}_\phi$ is the maximum amount of experts modified identically by $\phi$, and $d^{\mathrm{self}}_\phi$ is the amount of experts that $\phi$ trivially modifies to themselves. By recovering the optimal $O(\sqrt{T\log d})$ external regret bound when $d^{\mathrm{unif}}_\phi=d$, the standard $\tilde O(\sqrt{T})$ internal regret bound when $d^{\mathrm{self}}_\phi=d-1$ and the optimal $\tilde O(\sqrt{dT})$ swap regret bound in the worst case, we improve existing results in the intermediate regimes. In addition, the same algorithm achieves the optimal quantile regret bound, which corresponds to even easier settings of $\phi$ than the external regret. Building on the classical reduction from $\phi$-regret minimization to external regret minimization on stochastic matrices, our main idea is to further convert the latter to online linear regression using Haar-wavelet-inspired matrix features. Then, we apply a particular $L_1$-version of comparator-adaptive online learning algorithms to exploit the sparsity in this regression subroutine.

Tight Rates for Bandit Control Beyond Quadratics

Unlike classical control theory, such as Linear Quadratic Control (LQC), real-world control problems are highly complex. These problems often involve adversarial perturbations, bandit feedback models, and non-quadratic, adversarially chosen cost functions. A fundamental yet unresolved question is whether optimal regret can be achieved for these general control problems. The standard approach to addressing this problem involves a reduction to bandit convex optimization with memory. In the bandit setting, constructing a gradient estimator with low variance is challenging due to the memory structure and non-quadratic loss functions. In this paper, we provide an affirmative answer to this question. Our main contribution is an algorithm that achieves an $\tilde{O}(\sqrt{T})$ optimal regret for bandit non-stochastic control with strongly-convex and smooth cost functions in the presence of adversarial perturbations, improving the previously known $\tilde{O}(T^{2/3})$ regret bound from (Cassel and Koren, 2020. Our algorithm overcomes the memory issue by reducing the problem to Bandit Convex Optimization (BCO) without memory and addresses general strongly-convex costs using recent advancements in BCO from (Suggala et al., 2024). Along the way, we develop an improved algorithm for BCO with memory, which may be of independent interest.

Online Control in Population Dynamics

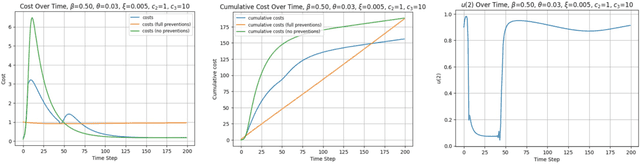
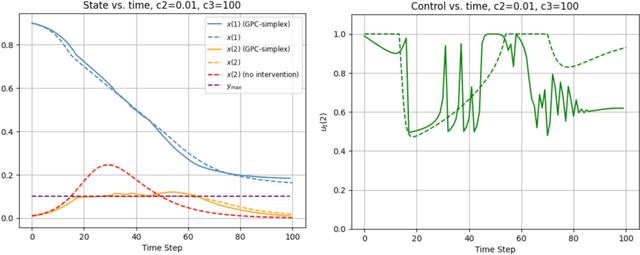
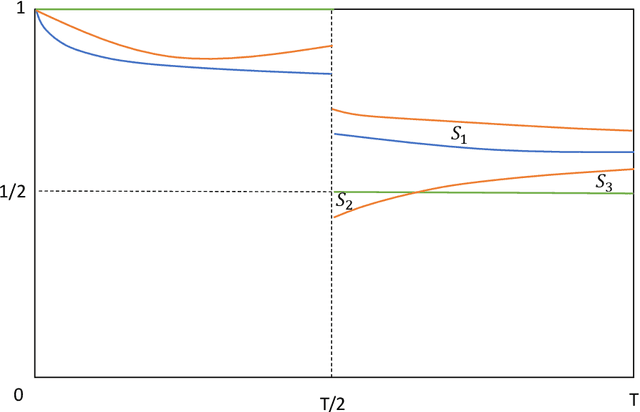
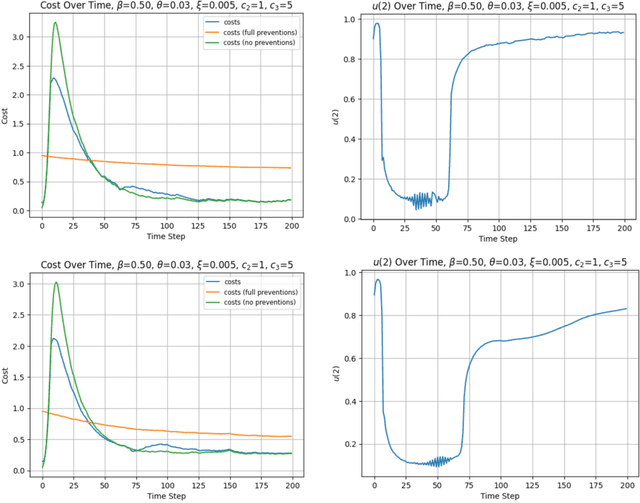
The study of population dynamics originated with early sociological works (Malthus, 1872) but has since extended into many fields, including biology, epidemiology, evolutionary game theory, and economics. Most studies on population dynamics focus on the problem of prediction rather than control. Existing mathematical models for population control are often restricted to specific, noise-free dynamics, while real-world population changes can be complex and adversarial. To address this gap, we propose a new framework based on the paradigm of online control. We first characterize a set of linear dynamical systems that can naturally model evolving populations. We then give an efficient gradient-based controller for these systems, with near-optimal regret bounds with respect to a broad class of linear policies. Our empirical evaluations demonstrate the effectiveness of the proposed algorithm for population control even in non-linear models such as SIR and replicator dynamics.

Second Order Methods for Bandit Optimization and Control

Bandit convex optimization (BCO) is a general framework for online decision making under uncertainty. While tight regret bounds for general convex losses have been established, existing algorithms achieving these bounds have prohibitive computational costs for high dimensional data. In this paper, we propose a simple and practical BCO algorithm inspired by the online Newton step algorithm. We show that our algorithm achieves optimal (in terms of horizon) regret bounds for a large class of convex functions that we call $\kappa$-convex. This class contains a wide range of practically relevant loss functions including linear, quadratic, and generalized linear models. In addition to optimal regret, this method is the most efficient known algorithm for several well-studied applications including bandit logistic regression. Furthermore, we investigate the adaptation of our second-order bandit algorithm to online convex optimization with memory. We show that for loss functions with a certain affine structure, the extended algorithm attains optimal regret. This leads to an algorithm with optimal regret for bandit LQR/LQG problems under a fully adversarial noise model, thereby resolving an open question posed in \citep{gradu2020non} and \citep{sun2023optimal}. Finally, we show that the more general problem of BCO with (non-affine) memory is harder. We derive a $\tilde{\Omega}(T^{2/3})$ regret lower bound, even under the assumption of smooth and quadratic losses.

Optimal Rates for Bandit Nonstochastic Control

Linear Quadratic Regulator (LQR) and Linear Quadratic Gaussian (LQG) control are foundational and extensively researched problems in optimal control. We investigate LQR and LQG problems with semi-adversarial perturbations and time-varying adversarial bandit loss functions. The best-known sublinear regret algorithm of~\cite{gradu2020non} has a $T^{\frac{3}{4}}$ time horizon dependence, and its authors posed an open question about whether a tight rate of $\sqrt{T}$ could be achieved. We answer in the affirmative, giving an algorithm for bandit LQR and LQG which attains optimal regret (up to logarithmic factors) for both known and unknown systems. A central component of our method is a new scheme for bandit convex optimization with memory, which is of independent interest.

Sketchy: Memory-efficient Adaptive Regularization with Frequent Directions

Adaptive regularization methods that exploit more than the diagonal entries exhibit state of the art performance for many tasks, but can be prohibitive in terms of memory and running time. We find the spectra of the Kronecker-factored gradient covariance matrix in deep learning (DL) training tasks are concentrated on a small leading eigenspace that changes throughout training, motivating a low-rank sketching approach. We describe a generic method for reducing memory and compute requirements of maintaining a matrix preconditioner using the Frequent Directions (FD) sketch. Our technique allows interpolation between resource requirements and the degradation in regret guarantees with rank $k$: in the online convex optimization (OCO) setting over dimension $d$, we match full-matrix $d^2$ memory regret using only $dk$ memory up to additive error in the bottom $d-k$ eigenvalues of the gradient covariance. Further, we show extensions of our work to Shampoo, placing the method on the memory-quality Pareto frontier of several large scale benchmarks.