Defect-aware Hybrid Prompt Optimization via Progressive Tuning for Zero-Shot Multi-type Anomaly Detection and Segmentation

Recent vision language models (VLMs) like CLIP have demonstrated impressive anomaly detection performance under significant distribution shift by utilizing high-level semantic information through text prompts. However, these models often neglect fine-grained details, such as which kind of anomalies, like "hole", "cut", "scratch" that could provide more specific insight into the nature of anomalies. We argue that recognizing fine-grained anomaly types 1) enriches the representation of "abnormal" with structured semantics, narrowing the gap between coarse anomaly signals and fine-grained defect categories; 2) enables manufacturers to understand the root causes of the anomaly and implement more targeted and appropriate corrective measures quickly. While incorporating such detailed semantic information is crucial, designing handcrafted prompts for each defect type is both time-consuming and susceptible to human bias. For this reason, we introduce DAPO, a novel approach for Defect-aware Prompt Optimization based on progressive tuning for the zero-shot multi-type and binary anomaly detection and segmentation under distribution shifts. Our approach aligns anomaly-relevant image features with their corresponding text semantics by learning hybrid defect-aware prompts with both fixed textual anchors and learnable token embeddings. We conducted experiments on public benchmarks (MPDD, VisA, MVTec-AD, MAD, and Real-IAD) and an internal dataset. The results suggest that compared to the baseline models, DAPO achieves a 3.7% average improvement in AUROC and average precision metrics at the image level under distribution shift, and a 6.5% average improvement in localizing novel anomaly types under zero-shot settings.

MultiADS: Defect-aware Supervision for Multi-type Anomaly Detection and Segmentation in Zero-Shot Learning

Precise optical inspection in industrial applications is crucial for minimizing scrap rates and reducing the associated costs. Besides merely detecting if a product is anomalous or not, it is crucial to know the distinct type of defect, such as a bent, cut, or scratch. The ability to recognize the "exact" defect type enables automated treatments of the anomalies in modern production lines. Current methods are limited to solely detecting whether a product is defective or not without providing any insights on the defect type, nevertheless detecting and identifying multiple defects. We propose MultiADS, a zero-shot learning approach, able to perform Multi-type Anomaly Detection and Segmentation. The architecture of MultiADS comprises CLIP and extra linear layers to align the visual- and textual representation in a joint feature space. To the best of our knowledge, our proposal, is the first approach to perform a multi-type anomaly segmentation task in zero-shot learning. Contrary to the other baselines, our approach i) generates specific anomaly masks for each distinct defect type, ii) learns to distinguish defect types, and iii) simultaneously identifies multiple defect types present in an anomalous product. Additionally, our approach outperforms zero/few-shot learning SoTA methods on image-level and pixel-level anomaly detection and segmentation tasks on five commonly used datasets: MVTec-AD, Visa, MPDD, MAD and Real-IAD.

ADEdgeDrop: Adversarial Edge Dropping for Robust Graph Neural Networks

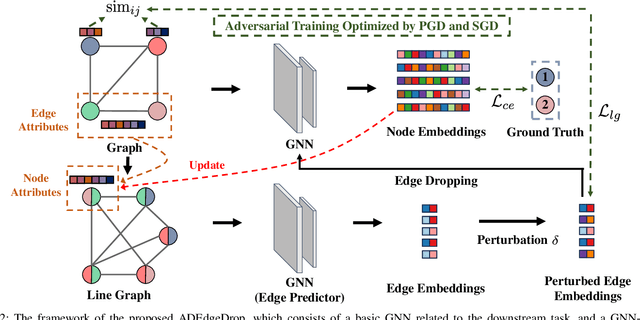
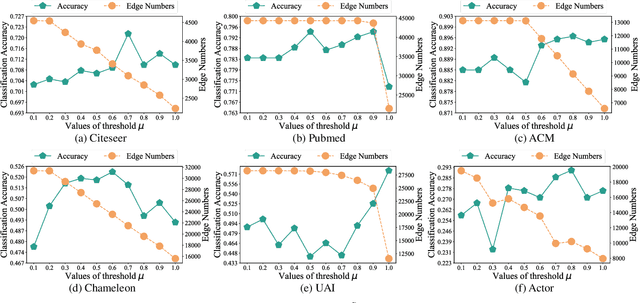
Although Graph Neural Networks (GNNs) have exhibited the powerful ability to gather graph-structured information from neighborhood nodes via various message-passing mechanisms, the performance of GNNs is limited by poor generalization and fragile robustness caused by noisy and redundant graph data. As a prominent solution, Graph Augmentation Learning (GAL) has recently received increasing attention. Among prior GAL approaches, edge-dropping methods that randomly remove edges from a graph during training are effective techniques to improve the robustness of GNNs. However, randomly dropping edges often results in bypassing critical edges, consequently weakening the effectiveness of message passing. In this paper, we propose a novel adversarial edge-dropping method (ADEdgeDrop) that leverages an adversarial edge predictor guiding the removal of edges, which can be flexibly incorporated into diverse GNN backbones. Employing an adversarial training framework, the edge predictor utilizes the line graph transformed from the original graph to estimate the edges to be dropped, which improves the interpretability of the edge-dropping method. The proposed ADEdgeDrop is optimized alternately by stochastic gradient descent and projected gradient descent. Comprehensive experiments on six graph benchmark datasets demonstrate that the proposed ADEdgeDrop outperforms state-of-the-art baselines across various GNN backbones, demonstrating improved generalization and robustness.

Spectral Clustering of Attributed Multi-relational Graphs

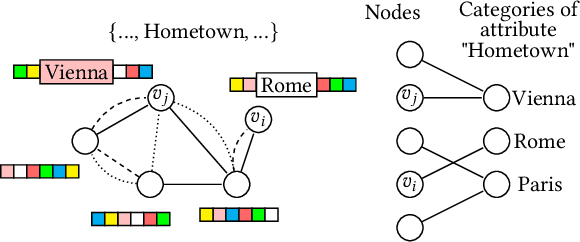
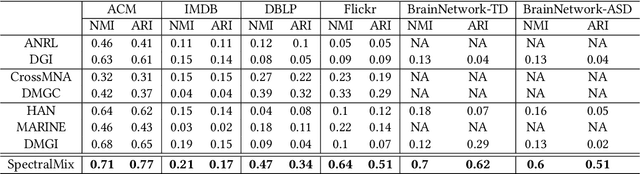
Graph clustering aims at discovering a natural grouping of the nodes such that similar nodes are assigned to a common cluster. Many different algorithms have been proposed in the literature: for simple graphs, for graphs with attributes associated to nodes, and for graphs where edges represent different types of relations among nodes. However, complex data in many domains can be represented as both attributed and multi-relational networks. In this paper, we propose SpectralMix, a joint dimensionality reduction technique for multi-relational graphs with categorical node attributes. SpectralMix integrates all information available from the attributes, the different types of relations, and the graph structure to enable a sound interpretation of the clustering results. Moreover, it generalizes existing techniques: it reduces to spectral embedding and clustering when only applied to a single graph and to homogeneity analysis when applied to categorical data. Experiments conducted on several real-world datasets enable us to detect dependencies between graph structure and categorical attributes, moreover, they exhibit the superiority of SpectralMix over existing methods.

Generalized Laplacian Positional Encoding for Graph Representation Learning

Graph neural networks (GNNs) are the primary tool for processing graph-structured data. Unfortunately, the most commonly used GNNs, called Message Passing Neural Networks (MPNNs) suffer from several fundamental limitations. To overcome these limitations, recent works have adapted the idea of positional encodings to graph data. This paper draws inspiration from the recent success of Laplacian-based positional encoding and defines a novel family of positional encoding schemes for graphs. We accomplish this by generalizing the optimization problem that defines the Laplace embedding to more general dissimilarity functions rather than the 2-norm used in the original formulation. This family of positional encodings is then instantiated by considering p-norms. We discuss a method for calculating these positional encoding schemes, implement it in PyTorch and demonstrate how the resulting positional encoding captures different properties of the graph. Furthermore, we demonstrate that this novel family of positional encodings can improve the expressive power of MPNNs. Lastly, we present preliminary experimental results.