Sahar Behzadi
Spectral Clustering of Attributed Multi-relational Graphs
Nov 03, 2023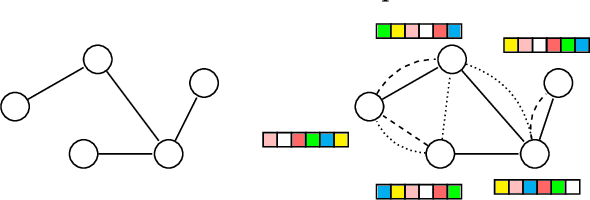

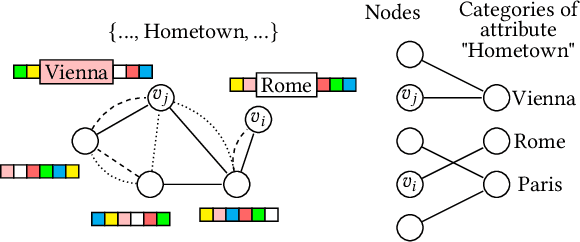
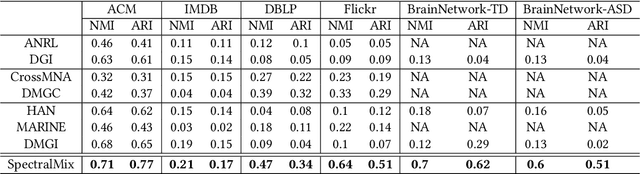
Abstract:Graph clustering aims at discovering a natural grouping of the nodes such that similar nodes are assigned to a common cluster. Many different algorithms have been proposed in the literature: for simple graphs, for graphs with attributes associated to nodes, and for graphs where edges represent different types of relations among nodes. However, complex data in many domains can be represented as both attributed and multi-relational networks. In this paper, we propose SpectralMix, a joint dimensionality reduction technique for multi-relational graphs with categorical node attributes. SpectralMix integrates all information available from the attributes, the different types of relations, and the graph structure to enable a sound interpretation of the clustering results. Moreover, it generalizes existing techniques: it reduces to spectral embedding and clustering when only applied to a single graph and to homogeneity analysis when applied to categorical data. Experiments conducted on several real-world datasets enable us to detect dependencies between graph structure and categorical attributes, moreover, they exhibit the superiority of SpectralMix over existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge