CMA-ES for Discrete and Mixed-Variable Optimization on Sets of Points

Discrete and mixed-variable optimization problems have appeared in several real-world applications. Most of the research on mixed-variable optimization considers a mixture of integer and continuous variables, and several integer handlings have been developed to inherit the optimization performance of the continuous optimization methods to mixed-integer optimization. In some applications, acceptable solutions are given by selecting possible points in the disjoint subspaces. This paper focuses on the optimization on sets of points and proposes an optimization method by extending the covariance matrix adaptation evolution strategy (CMA-ES), termed the CMA-ES on sets of points (CMA-ES-SoP). The CMA-ES-SoP incorporates margin correction that maintains the generation probability of neighboring points to prevent premature convergence to a specific non-optimal point, which is an effective integer-handling technique for CMA-ES. In addition, because margin correction with a fixed margin value tends to increase the marginal probabilities for a portion of neighboring points more than necessary, the CMA-ES-SoP updates the target margin value adaptively to make the average of the marginal probabilities close to a predefined target probability. Numerical simulations demonstrated that the CMA-ES-SoP successfully optimized the optimization problems on sets of points, whereas the naive CMA-ES failed to optimize them due to premature convergence.

CMA-ES for Safe Optimization

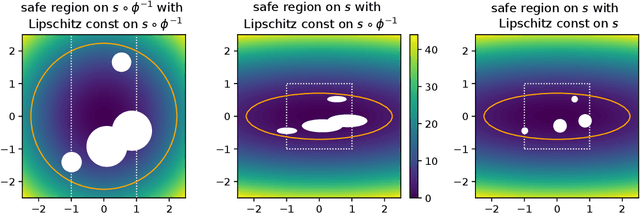
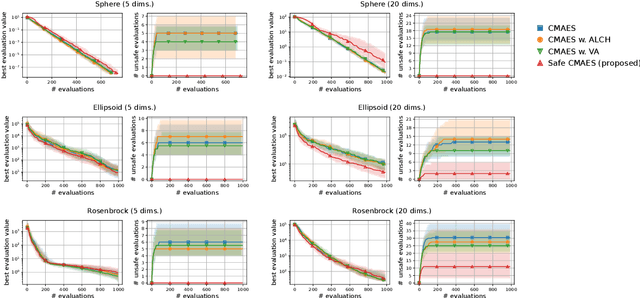
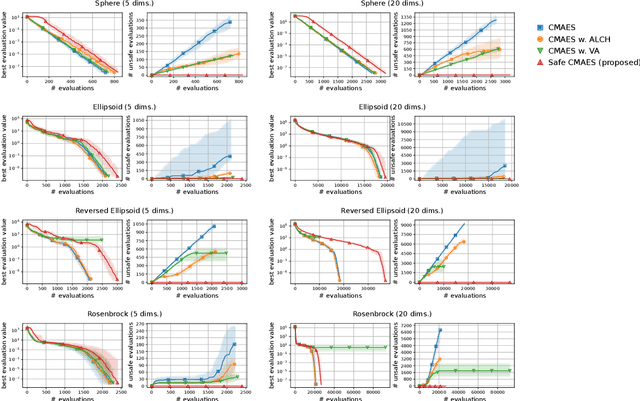
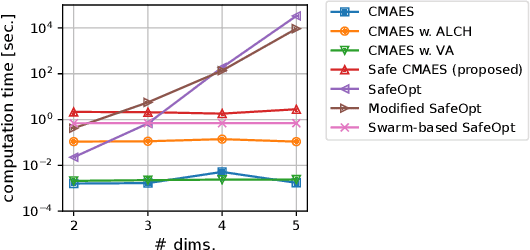
In several real-world applications in medical and control engineering, there are unsafe solutions whose evaluations involve inherent risk. This optimization setting is known as safe optimization and formulated as a specialized type of constrained optimization problem with constraints for safety functions. Safe optimization requires performing efficient optimization without evaluating unsafe solutions. A few studies have proposed the optimization methods for safe optimization based on Bayesian optimization and the evolutionary algorithm. However, Bayesian optimization-based methods often struggle to achieve superior solutions, and the evolutionary algorithm-based method fails to effectively reduce unsafe evaluations. This study focuses on CMA-ES as an efficient evolutionary algorithm and proposes an optimization method termed safe CMA-ES. The safe CMA-ES is designed to achieve both safety and efficiency in safe optimization. The safe CMA-ES estimates the Lipschitz constants of safety functions transformed with the distribution parameters using the maximum norm of the gradient in Gaussian process regression. Subsequently, the safe CMA-ES projects the samples to the nearest point in the safe region constructed with the estimated Lipschitz constants. The numerical simulation using the benchmark functions shows that the safe CMA-ES successfully performs optimization, suppressing the unsafe evaluations, while the existing methods struggle to significantly reduce the unsafe evaluations.

CatCMA : Stochastic Optimization for Mixed-Category Problems

Black-box optimization problems often require simultaneously optimizing different types of variables, such as continuous, integer, and categorical variables. Unlike integer variables, categorical variables do not necessarily have a meaningful order, and the discretization approach of continuous variables does not work well. Although several Bayesian optimization methods can deal with mixed-category black-box optimization (MC-BBO), they suffer from a lack of scalability to high-dimensional problems and internal computational cost. This paper proposes CatCMA, a stochastic optimization method for MC-BBO problems, which employs the joint probability distribution of multivariate Gaussian and categorical distributions as the search distribution. CatCMA updates the parameters of the joint probability distribution in the natural gradient direction. CatCMA also incorporates the acceleration techniques used in the covariance matrix adaptation evolution strategy (CMA-ES) and the stochastic natural gradient method, such as step-size adaptation and learning rate adaptation. In addition, we restrict the ranges of the categorical distribution parameters by margin to prevent premature convergence and analytically derive a promising margin setting. Numerical experiments show that the performance of CatCMA is superior and more robust to problem dimensions compared to state-of-the-art Bayesian optimization algorithms.

Bandits with Abstention under Expert Advice

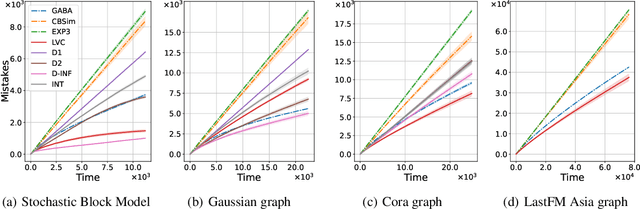
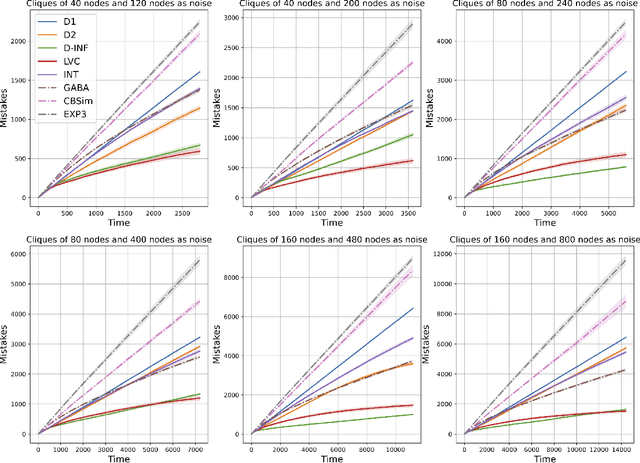
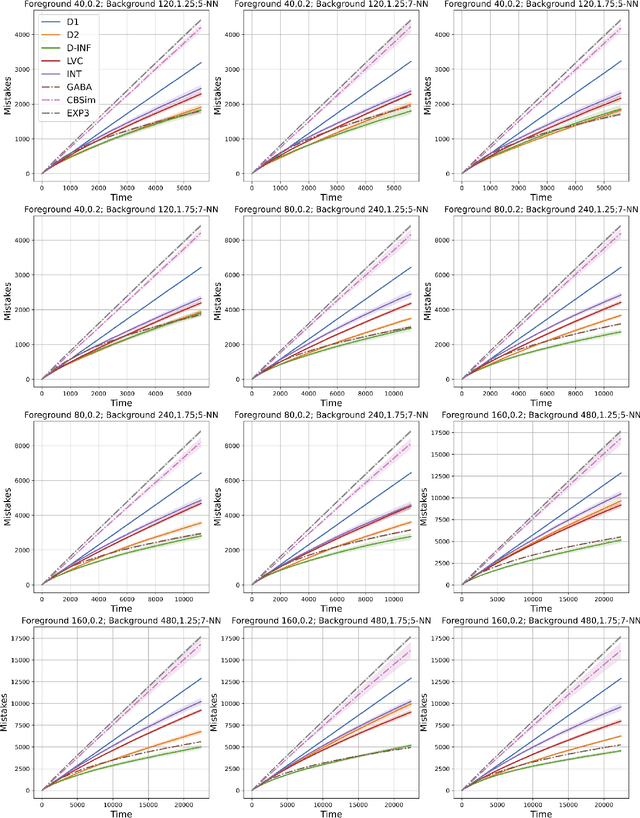
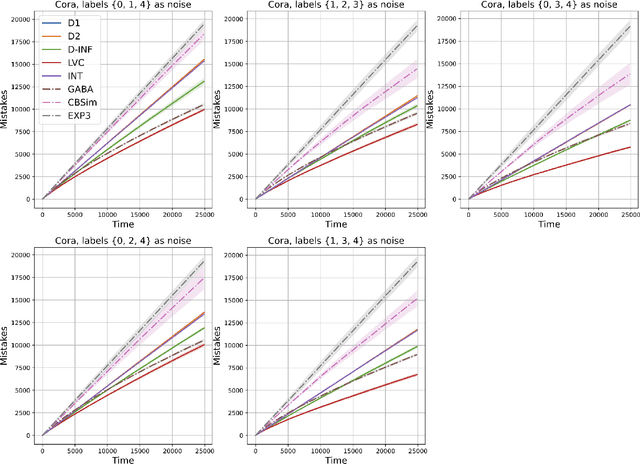
We study the classic problem of prediction with expert advice under bandit feedback. Our model assumes that one action, corresponding to the learner's abstention from play, has no reward or loss on every trial. We propose the CBA algorithm, which exploits this assumption to obtain reward bounds that can significantly improve those of the classical Exp4 algorithm. We can view our problem as the aggregation of confidence-rated predictors when the learner has the option of abstention from play. Importantly, we are the first to achieve bounds on the expected cumulative reward for general confidence-rated predictors. In the special case of specialists we achieve a novel reward bound, significantly improving previous bounds of SpecialistExp (treating abstention as another action). As an example application, we discuss learning unions of balls in a finite metric space. In this contextual setting, we devise an efficient implementation of CBA, reducing the runtime from quadratic to almost linear in the number of contexts. Preliminary experiments show that CBA improves over existing bandit algorithms.

Multi-class Graph Clustering via Approximated Effective $p$-Resistance

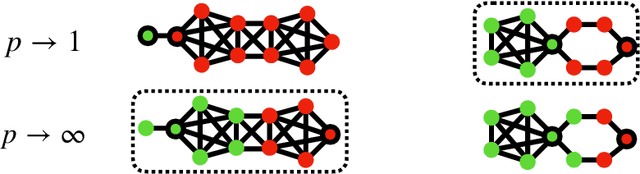
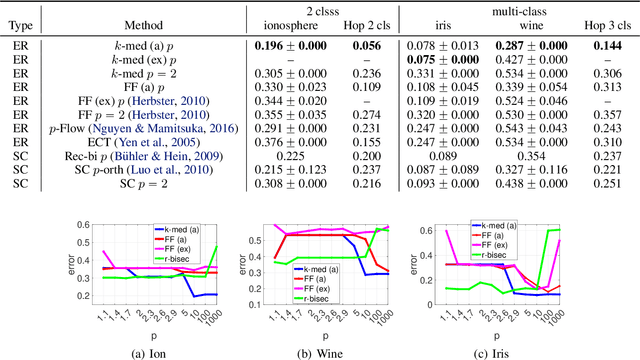
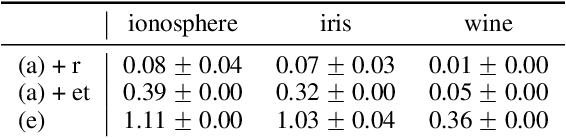
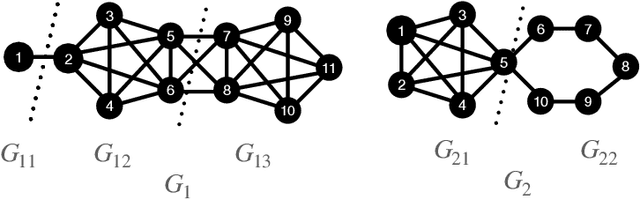
This paper develops an approximation to the (effective) $p$-resistance and applies it to multi-class clustering. Spectral methods based on the graph Laplacian and its generalization to the graph $p$-Laplacian have been a backbone of non-euclidean clustering techniques. The advantage of the $p$-Laplacian is that the parameter $p$ induces a controllable bias on cluster structure. The drawback of $p$-Laplacian eigenvector based methods is that the third and higher eigenvectors are difficult to compute. Thus, instead, we are motivated to use the $p$-resistance induced by the $p$-Laplacian for clustering. For $p$-resistance, small $p$ biases towards clusters with high internal connectivity while large $p$ biases towards clusters of small ``extent,'' that is a preference for smaller shortest-path distances between vertices in the cluster. However, the $p$-resistance is expensive to compute. We overcome this by developing an approximation to the $p$-resistance. We prove upper and lower bounds on this approximation and observe that it is exact when the graph is a tree. We also provide theoretical justification for the use of $p$-resistance for clustering. Finally, we provide experiments comparing our approximated $p$-resistance clustering to other $p$-Laplacian based methods.

Prediction Algorithms Achieving Bayesian Decision Theoretical Optimality Based on Decision Trees as Data Observation Processes

In the field of decision trees, most previous studies have difficulty ensuring the statistical optimality of a prediction of new data and suffer from overfitting because trees are usually used only to represent prediction functions to be constructed from given data. In contrast, some studies, including this paper, used the trees to represent stochastic data observation processes behind given data. Moreover, they derived the statistically optimal prediction, which is robust against overfitting, based on the Bayesian decision theory by assuming a prior distribution for the trees. However, these studies still have a problem in computing this Bayes optimal prediction because it involves an infeasible summation for all division patterns of a feature space, which is represented by the trees and some parameters. In particular, an open problem is a summation with respect to combinations of division axes, i.e., the assignment of features to inner nodes of the tree. We solve this by a Markov chain Monte Carlo method, whose step size is adaptively tuned according to a posterior distribution for the trees.

-CMA-ES with Margin for Discrete and Mixed-Integer Problems

The covariance matrix adaptation evolution strategy (CMA-ES) is an efficient continuous black-box optimization method. The CMA-ES possesses many attractive features, including invariance properties and a well-tuned default hyperparameter setting. Moreover, several components to specialize the CMA-ES have been proposed, such as noise handling and constraint handling. To utilize these advantages in mixed-integer optimization problems, the CMA-ES with margin has been proposed. The CMA-ES with margin prevents the premature convergence of discrete variables by the margin correction, in which the distribution parameters are modified to leave the generation probability for changing the discrete variable. The margin correction has been applied to ($\mu/\mu_\mathrm{w}$,$\lambda$)-CMA-ES, while this paper introduces the margin correction into (1+1)-CMA-ES, an elitist version of CMA-ES. The (1+1)-CMA-ES is often advantageous for unimodal functions and can be computationally less expensive. To tackle the performance deterioration on mixed-integer optimization, we use the discretized elitist solution as the mean of the sampling distribution and modify the margin correction not to move the elitist solution. The numerical simulation using benchmark functions on mixed-integer, integer, and binary domains shows that (1+1)-CMA-ES with margin outperforms the CMA-ES with margin and is better than or comparable with several specialized methods to a particular search domain.

CMA-ES with Margin for Single-and Multi-Objective Mixed-Integer Black-Box Optimization

This study targets the mixed-integer black-box optimization (MI-BBO) problem where continuous and integer variables should be optimized simultaneously. The CMA-ES, our focus in this study, is a population-based stochastic search method that samples solution candidates from a multivariate Gaussian distribution (MGD), which shows excellent performance in continuous BBO. The parameters of MGD, mean and (co)variance, are updated based on the evaluation value of candidate solutions in the CMA-ES. If the CMA-ES is applied to the MI-BBO with straightforward discretization, however, the variance corresponding to the integer variables becomes much smaller than the granularity of the discretization before reaching the optimal solution, which leads to the stagnation of the optimization. In particular, when binary variables are included in the problem, this stagnation more likely occurs because the granularity of the discretization becomes wider, and the existing modification to the CMA-ES does not address this stagnation. To overcome these limitations, we propose a simple extension of the CMA-ES based on lower-bounding the marginal probabilities associated with the generation of integer variables in the MGD. The numerical experiments on the MI-BBO benchmark problems demonstrate the efficiency and robustness of the proposed method. Furthermore, in order to demonstrate the generality of the idea of the proposed method, in addition to the single-objective optimization case, we incorporate it into multi-objective CMA-ES and verify its performance on bi-objective mixed-integer benchmark problems.

Neural Architecture Search for Improving Latency-Accuracy Trade-off in Split Computing

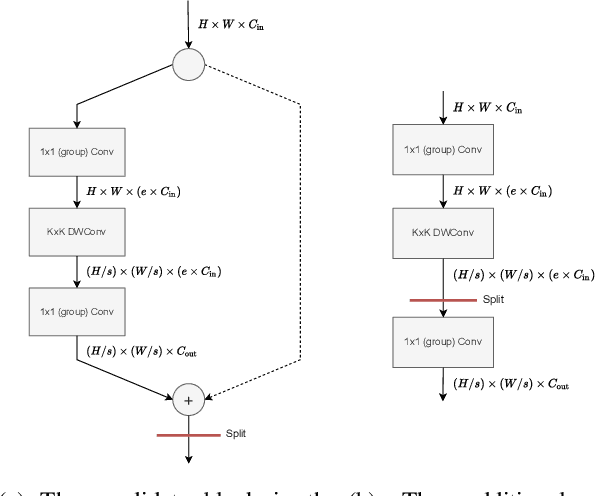
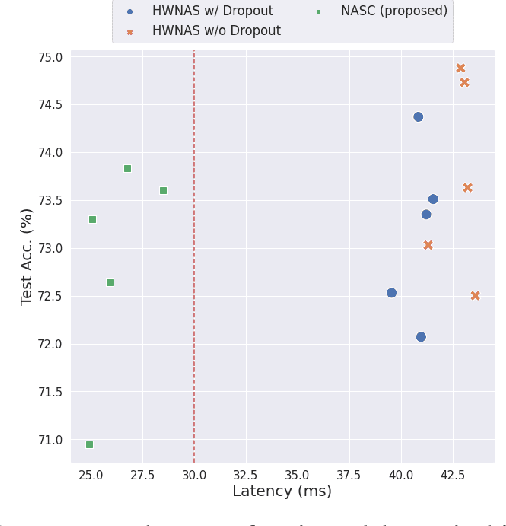
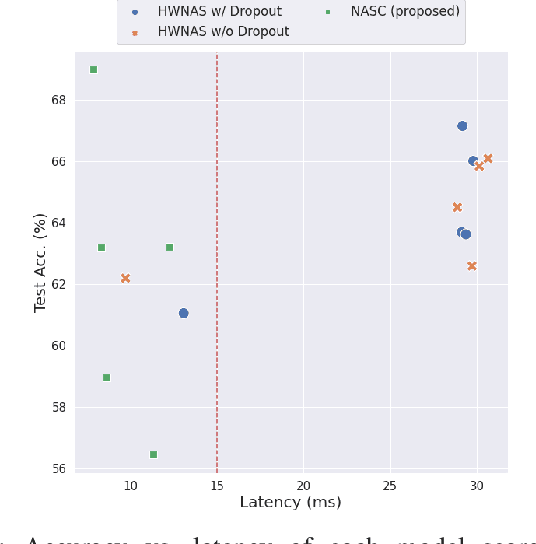
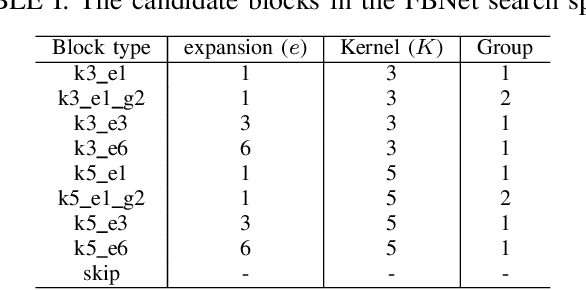
This paper proposes a neural architecture search (NAS) method for split computing. Split computing is an emerging machine-learning inference technique that addresses the privacy and latency challenges of deploying deep learning in IoT systems. In split computing, neural network models are separated and cooperatively processed using edge servers and IoT devices via networks. Thus, the architecture of the neural network model significantly impacts the communication payload size, model accuracy, and computational load. In this paper, we address the challenge of optimizing neural network architecture for split computing. To this end, we proposed NASC, which jointly explores optimal model architecture and a split point to achieve higher accuracy while meeting latency requirements (i.e., smaller total latency of computation and communication than a certain threshold). NASC employs a one-shot NAS that does not require repeating model training for a computationally efficient architecture search. Our performance evaluation using hardware (HW)-NAS-Bench of benchmark data demonstrates that the proposed NASC can improve the ``communication latency and model accuracy" trade-off, i.e., reduce the latency by approximately 40-60% from the baseline, with slight accuracy degradation.

Efficient Search of Multiple Neural Architectures with Different Complexities via Importance Sampling

Neural architecture search (NAS) aims to automate architecture design processes and improve the performance of deep neural networks. Platform-aware NAS methods consider both performance and complexity and can find well-performing architectures with low computational resources. Although ordinary NAS methods result in tremendous computational costs owing to the repetition of model training, one-shot NAS, which trains the weights of a supernetwork containing all candidate architectures only once during the search process, has been reported to result in a lower search cost. This study focuses on the architecture complexity-aware one-shot NAS that optimizes the objective function composed of the weighted sum of two metrics, such as the predictive performance and number of parameters. In existing methods, the architecture search process must be run multiple times with different coefficients of the weighted sum to obtain multiple architectures with different complexities. This study aims at reducing the search cost associated with finding multiple architectures. The proposed method uses multiple distributions to generate architectures with different complexities and updates each distribution using the samples obtained from multiple distributions based on importance sampling. The proposed method allows us to obtain multiple architectures with different complexities in a single architecture search, resulting in reducing the search cost. The proposed method is applied to the architecture search of convolutional neural networks on the CIAFR-10 and ImageNet datasets. Consequently, compared with baseline methods, the proposed method finds multiple architectures with varying complexities while requiring less computational effort.